Похідна функцій заданих неявно і параметрично - Основи вищої математики
І. Нехай значення двох змінних Х и Y зв'язані між собою деяким рівнянням
F(Х,Y)=0. (13.1)
Якщо функція Y=F(Х) визначена на інтервалі (А,B) така, що рівняння (13.1) при підстановці в нього замість Y F(Х) звертається в тотожність відносно Х, то функція Y=F(Х) є Неявна функція, обумовлена рівнянням (13.1).
Наприклад:
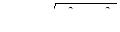
X2+Y2--A2=0, підставимо X2+Y2--X2--A2=0.
Зауваження 1. Відзначимо, що терміни "явна функція" й "неявна функція" характеризують не природу функції, а спосіб завдання. Кожна явна функція Y=F(Х) може бути представлена як неявна: Y--F(Х) =0.
Правило знаходження похідної неявної функції, не перетворюючи її в явну таке. Нехай функція задана рівнянням X2+Y2--A2=0. Тут Y є функція від Х, що визначає і цю тотожність.
Взявши похідну по Х, вважаючи, що Y є функція Х, користуючись складною функцією, одержимо:
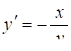
2X+2Yy =0 .
Ще приклад:
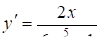
Y6--Y--X2=0 6Y5Y --Y --2X=0 .
Зауваження 2. З наведених прикладів випливає, що для знаходження значення похідної неявної функції при даному значенні аргументу Х потрібно знати і значення функції Y при даному значенні Х.
ІІ. Похідна функції, заданої параметрично.
Нехай функція Y від Х задана параметричними рівняннями
X=(T), Y=(T), T0TT. (13.2)
Припустимо, що ці функції мають похідні й що функція X=(T) має зворотну T=(Х), що також має похідну. Тоді, визначену параметричними рівняннями функцію Y=F(X) можна розглядати як складну функцію y=(T), T=(Х), де T -- проміжний аргумент. Тоді за правилом складної функції
. (13.3)
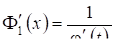
На основі теореми про похідну зворотньої функції. Підставляючи, одержимо
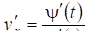
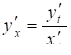
або. (13.4)
Введена формула дає можливість знаходити похідну функції, заданої параметрично, не знаходячи виразу безпосередньої залежності Y від Х.
Приклад: Знайти кутовий коефіцієнт дотичної до лінії, заданої
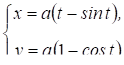
у точці 0T2.
.
Похожие статьи
-
Теорема 1. Похідна від функції logax дорівнює, тобто якщо y=logax, то . (11.1) Теорема 2. Похідна від sinx є cosx, тобто якщо y=sinx, то Y =cosx. (11.2)...
-
Похідна. Її фізична (механічна) і геометрична інтерпретація - Основи вищої математики
І. Вважаючи, що X 0, розглянемо в даній фіксованій точці " Х " відношення приросту функції в цій точці до відповідного приросту аргументу Х . (7.1) (7.1)...
-
Теорема 1. Похідна Const =0, тобто якщо Y = С, те Y =0, де С = Const . Y = С -- пряма паралельна осі ОХ й Tg =0, тобто F ( Х) =0. Теорема 2. Постійний...
-
Похідна в економіці - Основи вищої математики
Розглянемо однофакторну або одноресурсну похідну функцію Y = F ( Х) , що дає об'єм виробленої продукції за одиницю часу залежно від об'єму Х витраченого...
-
Безперервність функції - Основи вищої математики
Нехай функція Y = F ( Х) визначена при деякому значенні Х 0 й у деякій околиці із центром у Х 0, нехай Y 0= F ( Х 0). Якщо Х одержить деякий позитивний...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Межа функції - Основи вищої математики
Розглянемо деякі випадки зміни функції або прагнення аргументу Х до деякої межі " А " або до. Визначення 1: Нехай функція y=f(х) визначена в деякій...
-
Пряма на площині. Площина в просторі - Основи вищої математики
Пряма в просторі І. Пряма на площині 1. Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору Нехай на площині ХО задана точка М...
-
Розкриття невизначеностей. Формула Тейлора - Основи вищої математики
1. Невизначеність виду 0/0. Теорема 1 ( Правило Лопіталя - Гійом 1661-1704 р., французький математик, автор першого друкованого підручника по...
-
Точки розриву і їхня класифікація. Теореми про безперервні функції - Основи вищої математики
Якщо функція F така, що для неї існують межі F ( А +0) і F ( А --0), однак F ( А ) F ( А +0) F ( А --0), то, мабуть, вона нерозривна (не безперервна) у...
-
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ, Поняття межі послідовності - Основи вищої математики
Математика алгебра геометрія тригонометрія Поняття межі послідовності Визначення : Нехай кожному натуральному числу n=1, 2, 3, ... за деяким законом...
-
Дослідження функції однієї змінної за допомогою першої й другої похідних - Основи вищої математики
I. Ознаки сталості зростання й спадання функції Теорема 1. Якщо у всіх точках проміжку A < X < B похідна F ( Х) = 0, то функція F ( Х) зберігає в...
-
А) Представлення у вигляді многочлена, тобто можна представити у вигляді многочлена за допомогою елементарних перетворень (приведеня подібних членів і...
-
Диференціал функції y = f (x) в точці х називається головна частина її приросту, рівна добутку похідної функції на приріст аргументу, і про-значущих dy...
-
Метод Гауса - Основи вищої математики
( Карл Фрідріх Гаус (1777-1855) іноземний член Петербурзької АН (1824), німецький математик. Праці: вища алгебра, диференціальна геометрія, математична...
-
Визначення : Нехай дана матриця А=(mn), тоді мінором порядку "k" називають визначник, складений з елементів цієї матриці, якщо в неї викреслити (m--k)...
-
І. Визначення : Окружністю називається множина всіх точок площини, що перебувають на однаковій відстані, названій Радіусом , від фіксованої точки,...
-
Асимптоти. Вертикальні й горизонтальні - Основи вищої математики
Якщо відстань ОМ від деякої точки О до точки, що Рухається, М, то Відстань О 1 М , на яку Точка М віддаляється від якої-небудь іншої нерухомої Крапки О 1...
-
Пряма в просторі - Основи вищої математики
І. Загальне рівняння прямої Пряму в просторі найчастіше задають як перетинання двох площин І площина А 1 Х + В 1 Y + C 1 Z + D =0 ІІ площина А 2 Х + В 2...
-
Визначення. Матриця називається оберненою матриці, якщо їх добуток, тобто рівний одиничній матриці. Якщо квадратна матриця має зворотню матрицю, то вона...
-
Рівняння, Трансцендентні рівняння - Основи вищої математики
З одним невідомим повинно бути одне, його звичайно приводять до канонічного вигляду: Приклад: Рівняння 1,2,3 ... степені і т. д. -- лінійні рівняння....
-
Теореми про межі. Чудові межі - Основи вищої математики
Будемо розглядати сукупність функцій, які залежать від того самого аргументу Х , при цьому Ха або Х . Доведення проводиться для одного із цих випадків,...
-
Системи лінійних алгебраїчних рівнянь - Основи вищої математики
1. Будемо розглядати систему з "m" лінійних алгебраїчних рівнянь із "n" невідомими (8.1) Рішенням такої системи називається такий набір чисел Х 1, Х 2,...
-
: Елементарна математика, Основні поняття - Основи вищої математики
Основні поняття Визначення. Алгебраїчним виразом називається одна чи декілька алгебраїчних велечин (чисел чи букв) з'єднаних між собою знаками...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
Вектори. Лінійні операції над векторами, лінійні залежності векторів - Основи вищої математики
Визначення : У фізиці Векторними величинами або Векторами називаються ті, які характеризуються не тільки їхнім числовим значенням, але й напрямком у...
-
І. Визначення : Мішаним добутком трьох векторів і називається добуток виду, де два перших вектори перемножуються векторно, а їхній добуток множиться...
-
Знаходження границь та частинних похідних і диференціалів функцій двох змінних
Знаходження границь та частинних похідних і диференціалів функцій двох змінних Будь-який упорядкований набір з П Дійсних чисел Х 1 ,...,x N позначається...
-
Визначники та їх властивості - Основи вищої математики
До поняття визначника приходимо, розглядаючи системи алгебраїчних рівнянь першого степеня. Розглянемо систему рівнянь: (2.1) X та y -- невідомі,...
-
Матриці. Дії над матрицями Матриця вперше з'явилась в середині ХІХ століття в роботах англійських математиків У. Гамільтона і А. Келі [У. Гамільтон,...
-
Нескінченно мала й нескінченно велика величини - Основи вищої математики
Визначення . Змінна N , що має межу рівну 0, називається нескінченно малою величиною, якщо для кожного > 0 знайдеться n 0 таке, що | N |< ( N > N 0) ....
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
Загальні властивості функцій - Функції та способи їх задання
Означення : Множина всіх значень аргумента, для яких можна обчислити значення функції, називається природною областю визначення функції. Область...
-
Аргумент, функція, похідна - Математичний аналіз
Різниця між двома аргументами називається приростом аргументу. Приростом функції називається різниця між двома значеннями функції. Нехай в деякому околі...
-
Теорема 1. Нехай послідовності (хП) і (уП) мають відповідно границі а і b. Тоді послідовність (xN+yN) має границю а + b. Теорема 2. Нехай послідовності...
-
Приклад 1. Хай Тоді при кожному Приклад 2. Хай графік функції F(x) Має вигляд, зображений на рис.8.1. Тоді графік функції показаний на рис.8.2. Мал. 8.1....
-
У роботі розглядаються безперервні функції F З періодом 2p і їх наближення тригонометричними поліномами. Через Tn(x) Позначається тригонометричний...
-
Інтегрування частинами, Заміна змінної у визначеному інтегралі - Визначений інтеграл
Якщо проінтегрувати обидві частини рівності D[u(x) - v(x)] = v(x)du(x) + u(x)dv(x) В межах від А до B , то одержимо Звідси одержуємо важливу формулу...
-
У цьому параграфі узагальнюються і уточнюються так звані "зворотні теореми" теорії наближення. Мова йде про оцінці диференціальних властивостей функції f...
Похідна функцій заданих неявно і параметрично - Основи вищої математики