Пряма на площині. Площина в просторі - Основи вищої математики
Пряма в просторі
І. Пряма на площині
1. Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору
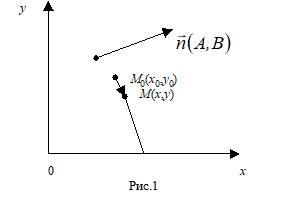
Нехай на площині ХО задана точка М0(Х0,Y0) і вектор (A,B). Запишемо рівняння прямої, що проходить через М0 перпендикулярно вектору.
Рівнянням прямої буде таке рівняння, якому задовольнять координати кожної точки, що лежить на цій прямій, і не задовольняють координати будь-якої точки, що не лежить на цій прямій. Для складання рівняння візьмемо точку М(Х,Y). Розглянемо вектор (X--X0,Y--Y0). Тоді для прямої необхідна умова
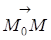
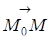
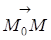
( )=(X--X0)A+(Y--Y0)B=0. (13.1)
Це і є шукане рівняння.
2. Загальне рівняння прямої. Пряма як лінія першого порядку. Окремі випадки рівняння прямої.
З рівняння (13.1) одержимо, розкривши дужки
Ax+By--Ax0--Bx0=0 Ax+Bx+C=0. (13.2)
Число
Рівняння (13.2) і є загальне рівняння прямої на площині.
Зауваження: Лінія, рівняння якої є рівняння першого степеня, називається лінією першого порядку.
Якщо дано рівняння першого степеня, то коефіцієнти при змінних Х и Y -- це А и В, які є коефіцієнтами вектора перпендикулярного цій прямій.
Приклад: 5Х--7Y+8=0, те (5,-7).
Рівняння прямої, що проходить через дану крапку паралельно даному вектору.
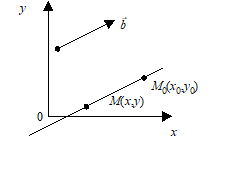
Нехай пряма проходить через дану крапку М0(Х0,Y0) паралельно даному вектору (M,N). Тоді
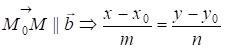
. (13.3)
Це умова паралельності векторів.
Приклад: М0(5,7), =(-2,3) те рівняння прямої буде
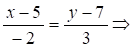
3Х+2Y--29=0.
4. Рівняння прямої, що проходить через дві точки
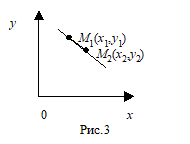
Тоді
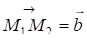
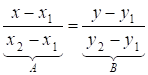
. (13.4)
5. Параметричне рівняння прямих.
Нехай дане рівняння. Тоді
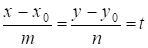
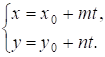
(13.5)
Це і є параметричне рівняння прямої, де T -- параметр.
Приклад: М0(5,7), =(-2,3).
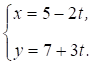
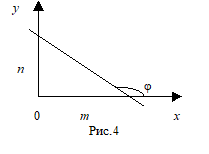
6. Рівняння прямої з кутовим коефіцієнтом.
Нехай пряма задана рівнянням
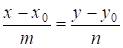
, n0.
Помножимо на "N", одержимо
N/M(X--X0)=Y--Y0,
N/M -- кутовий коефіцієнт, рівний K,
K=Tg,
Де -- кут нахилу прямої до осі ОХ. Тоді
Y--Y0= k(X--X0). (13.6)
Це і є рівняння прямої, що проходить через дану точку в заданому напрямку. Тоді
Kx--Kx0= y--Y0 Y=Kx+B,
Де B=Y0--X0.
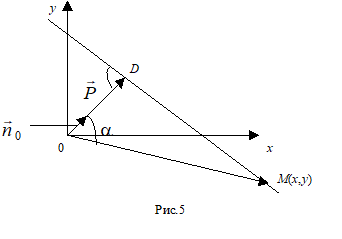
7. Нормоване рівняння прямої.
Нехай на площині дана пряма, не перпендикулярна осям координат.
Позначимо через Р довжину перпендикуляра, -- кут.
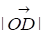
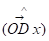
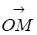
Знаючи Р и напишемо рівняння цієї прямої, розглядаючи радіус вектор, тоді проекція на буде
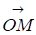
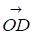
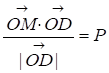
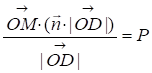
або,
| |=1, але 0=(Cos,Sin). Тоді можна записати
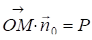
, (X,Y)(Cos,Sin)=P,
Xcos+Ysin=P. (13.7)
Це і є нормоване рівняння прямої. A= cos, B= sin.
8. Відстань від точки до прямої на площині.
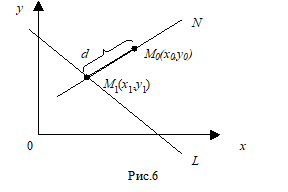
Задано пряму L, її рівняння Ах+Вy+С=0 і дана точка М0(Х0,Y0). Необхідно знайти D -- відстань від точки М0 до прямої L. Проведемо через М0 пряму перпендикулярну L й одержимо М1(Х1,Y1)
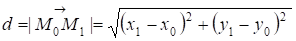
.
Але Х1 й Y1 -- невідомі. Тоді зробемо так, рівняння прямої NL і минаючої через М0(Х0,Y0) може бути записане у вигляді
В(Х-х0)-А(Y--Y0)=0.
Координати точки М1(Х1,Y1), у якій перетинаються прямі L й N повинні задовольняти рівнянням обох цих прямих, тобто
(*)
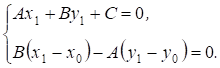
До першого рівняння додамо й віднімемо Ах0+Вy0. Тоді
(**) А(Х1-х0)+В(Y1--Y0)= --(Ах0+Вy0+С).
Для відшукання D піднесемо до квадрата другу з рівностей (*) і (**) і складемо почленно, одержимо
(A2+B2)[(X1--X0)2+(Y1--Y0)2]=(Ax0+Bx0+C)2.
D2
Тоді
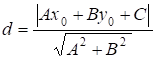
. (13.8)
Приклад: М0(1,-4). Визначити її відстань до прямої 4х--3y+12=0.
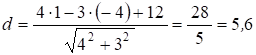
.
9. Рівняння прямої у відрізках (самостійно).
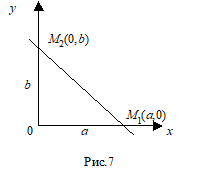
Припустимо, що відомо координати точок перетину прямої з осями координат: А -- з віссю ОХ, B -- з віссю ОY (їх називають відрізками прямої на осях координат). Складемо за цим даними рівняння прямої. Тому що нам відомі М1(А,0), М2(0,B) через які проходить пряма, то можна написати рівняння
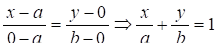
. (13.9)
Це рівняння називається Рівнянням у відрізках. Його використовують тоді, коли за параметри, що визначають положення прямої на координатній площині зручно прийняти відрізки, що відтинають пряма на осях координат.
10. Кут між прямими.
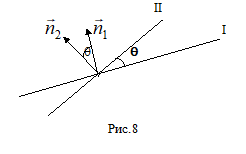
Нехай дані дві прямі
A1X+B1Y+C1=0 A2X+B2Y+C2=0
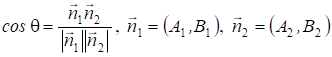
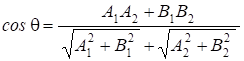
. (13.10)
Наприклад:
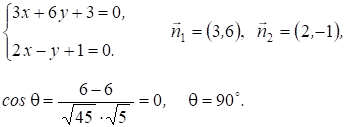
Зауваження: 1) Прямі перпендикулярні тоді й тільки тоді, коли Cos=0, тобто А1А2+В1B2=0
=2--1,
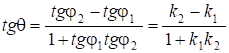
. (13.11)
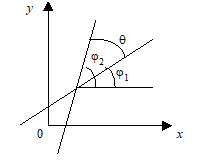
Якщо прямі паралельні, то Tg=0, тобто K2=K1, а перпендикулярні, то 1+
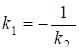
K1K2=0, .
ІІ. Площина в просторі
1. Рівняння площини, що проходить через точку перпендикулярно даному вектору

Нехай площина проходить через точку М0(Х0,Y0,Z0) і перпендикулярна =(A,B,C).
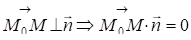
Візьмемо на площині точку М(Х,Y,Z), тоді.
A(X--X0)+B(Y--Y0)+C(Z--Z0)=0. (13.12)
2. Загальне рівняння площини. Площина як поверхня першого порядку. Окремі випадки загального рівняння.
Перетворимо рівняння (13.13). Одержимо
Ax+By+Cz+D=0, (13.13)
Де D= --(Ax0+By0+Cz0)=Const.
Це загальне рівняння площини, бачимо, що воно першого степеня відносно Х, Y, Z.
Справедливо й зворотне твердження: усяке рівняння першого степеня відносно Х, Y, Z є рівнянням площини.
Окремі випадки розглянути самостійно.
- 1. А=0 By+Cz+D=0 площина паралельна осі ОХ; В=0 || OY, С=0 || OZ. 2. D =0 -- площина проходить через початок координат. 3. А=В=0 Cz+D=0-- площина паралельна осям ОХ й ОY, тобто паралельна ХОY і перпендикулярна OZ рівняння Z=С.
А=C=0 ОY, В=C=0 ОХ й Y=B, X=A.
4. А=D=0 -- площина проходить через вісь ОХ, тобто вона паралельна ОХ і проходить через початок координат.
Аналогічно В=D=0 через ОY, C=D=0 через ОZ.
5. А=В=D=0 -- площина збігається з ХОY рівняння z=0.
А=C=D=0 ХОY, Y=0; C=В=D=0 YОZ, Х=0.
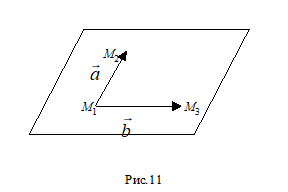
3. Рівняння площини, що проходить через дану точку паралельно двом даним векторам.
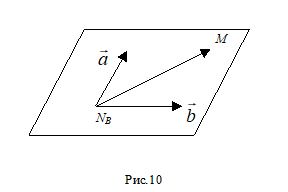
М0(Х0,Y0,Z0), =(AX,AY,AZ), =(BX,BY,BZ), М(Х,Y,Z)
, , -- компланарні, тобто паралельні одній площини. Тоді ( ) =0, тобто
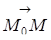
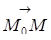
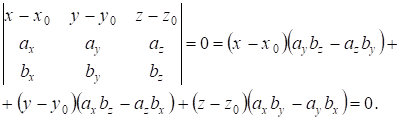
(13.14)
Рівняння площини, що проходить через три точки.
М1(Х1,Y1,Z1), М2(Х2,Y2,Z2), М3(Х3,Y3,Z3)
=[(X2--X1),(Y2--Y1),(Z2--Z1)],
=[(x3--x1),(y3--y1),(z3--z1)],

. (13.15)
Приклад: Написати рівняння площини, що проходить через точки А(-2,3,1), В(-1,0,2), З(1,-2,3).
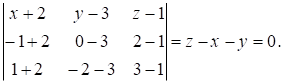
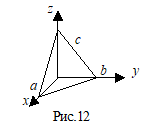
5. Рівняння площини у відрізках на осях.
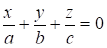
. (13.16)
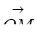
Візьмемо площину не минаючу через початок координат. перпендикулярний площині, -- одиничний вектор, Р=| | -- відстань від початку координат до площини, М(Х,Y,Z) -- довільна точка в просторі, -- радіус вектор, D -- відстань від точки М до площини.
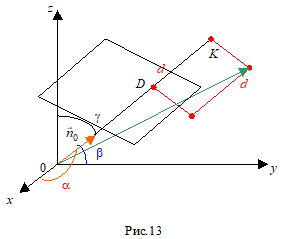
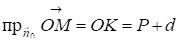
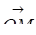
D=DK, , =(X,Y,Z), =(Cos,Cos,Cos).
У координатній формі
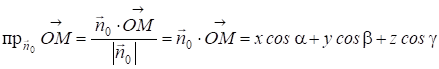
,
D=(Xcos+Ycos+Zcos--P). (13.17)
D= -- це відхилення точки від площини.
У випадку D=0 ми маємо рівняння, що справедливо для точок М(Х,Y,Z), що належать цій площині й тільки для неї і навпаки. Тоді
Xcos+Ycos+Zcos=P. (13.18)
Це нормоване рівняння площини.
Xcos+Ycos+Zcos--P=D. (13.19)
Рівняння площини, що відстоїть від даної точки на відстань d.
7. Кут між площинами.
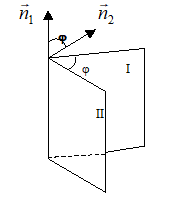
Цим кутом буде один з кутів між векторами, перпендикулярними до цих площин
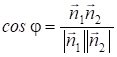
Нехай дані дві площини:
A1X+B1Y+C1Z+D1=0
A2X+B2Y+C2Z+D2=0
Вектора, перпендикулярні цим площинам:
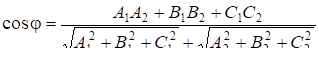
. (13.20)
- А) якщо площини перпендикулярні, то =0, тобто А1А2+В1B2+C1С2=0; Б) якщо площини паралельні -- координати векторів пропорційні
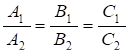
умова паралельності.
Похожие статьи
-
Пряма в просторі - Основи вищої математики
І. Загальне рівняння прямої Пряму в просторі найчастіше задають як перетинання двох площин І площина А 1 Х + В 1 Y + C 1 Z + D =0 ІІ площина А 2 Х + В 2...
-
І. Визначення : Окружністю називається множина всіх точок площини, що перебувають на однаковій відстані, названій Радіусом , від фіксованої точки,...
-
Теорема 1. Похідна від функції logax дорівнює, тобто якщо y=logax, то . (11.1) Теорема 2. Похідна від sinx є cosx, тобто якщо y=sinx, то Y =cosx. (11.2)...
-
Похідна. Її фізична (механічна) і геометрична інтерпретація - Основи вищої математики
І. Вважаючи, що X 0, розглянемо в даній фіксованій точці " Х " відношення приросту функції в цій точці до відповідного приросту аргументу Х . (7.1) (7.1)...
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
Асимптоти. Вертикальні й горизонтальні - Основи вищої математики
Якщо відстань ОМ від деякої точки О до точки, що Рухається, М, то Відстань О 1 М , на яку Точка М віддаляється від якої-небудь іншої нерухомої Крапки О 1...
-
Розкриття невизначеностей. Формула Тейлора - Основи вищої математики
1. Невизначеність виду 0/0. Теорема 1 ( Правило Лопіталя - Гійом 1661-1704 р., французький математик, автор першого друкованого підручника по...
-
Похідна функцій заданих неявно і параметрично - Основи вищої математики
І. Нехай значення двох змінних Х и Y зв'язані між собою деяким рівнянням F ( Х , Y )=0. (13.1) Якщо функція Y = F ( Х) визначена на інтервалі ( А , B )...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
Дослідження функції однієї змінної за допомогою першої й другої похідних - Основи вищої математики
I. Ознаки сталості зростання й спадання функції Теорема 1. Якщо у всіх точках проміжку A < X < B похідна F ( Х) = 0, то функція F ( Х) зберігає в...
-
Вектори. Лінійні операції над векторами, лінійні залежності векторів - Основи вищої математики
Визначення : У фізиці Векторними величинами або Векторами називаються ті, які характеризуються не тільки їхнім числовим значенням, але й напрямком у...
-
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ, Поняття межі послідовності - Основи вищої математики
Математика алгебра геометрія тригонометрія Поняття межі послідовності Визначення : Нехай кожному натуральному числу n=1, 2, 3, ... за деяким законом...
-
Визначення. Матриця називається оберненою матриці, якщо їх добуток, тобто рівний одиничній матриці. Якщо квадратна матриця має зворотню матрицю, то вона...
-
Метод Гауса - Основи вищої математики
( Карл Фрідріх Гаус (1777-1855) іноземний член Петербурзької АН (1824), німецький математик. Праці: вища алгебра, диференціальна геометрія, математична...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Точки розриву і їхня класифікація. Теореми про безперервні функції - Основи вищої математики
Якщо функція F така, що для неї існують межі F ( А +0) і F ( А --0), однак F ( А ) F ( А +0) F ( А --0), то, мабуть, вона нерозривна (не безперервна) у...
-
І. Визначення : Мішаним добутком трьох векторів і називається добуток виду, де два перших вектори перемножуються векторно, а їхній добуток множиться...
-
Похідна в економіці - Основи вищої математики
Розглянемо однофакторну або одноресурсну похідну функцію Y = F ( Х) , що дає об'єм виробленої продукції за одиницю часу залежно від об'єму Х витраченого...
-
Рівняння, Трансцендентні рівняння - Основи вищої математики
З одним невідомим повинно бути одне, його звичайно приводять до канонічного вигляду: Приклад: Рівняння 1,2,3 ... степені і т. д. -- лінійні рівняння....
-
А) Представлення у вигляді многочлена, тобто можна представити у вигляді многочлена за допомогою елементарних перетворень (приведеня подібних членів і...
-
Безперервність функції - Основи вищої математики
Нехай функція Y = F ( Х) визначена при деякому значенні Х 0 й у деякій околиці із центром у Х 0, нехай Y 0= F ( Х 0). Якщо Х одержить деякий позитивний...
-
Теореми про межі. Чудові межі - Основи вищої математики
Будемо розглядати сукупність функцій, які залежать від того самого аргументу Х , при цьому Ха або Х . Доведення проводиться для одного із цих випадків,...
-
Нескінченно мала й нескінченно велика величини - Основи вищої математики
Визначення . Змінна N , що має межу рівну 0, називається нескінченно малою величиною, якщо для кожного > 0 знайдеться n 0 таке, що | N |< ( N > N 0) ....
-
Теорема 1. Похідна Const =0, тобто якщо Y = С, те Y =0, де С = Const . Y = С -- пряма паралельна осі ОХ й Tg =0, тобто F ( Х) =0. Теорема 2. Постійний...
-
Межа функції - Основи вищої математики
Розглянемо деякі випадки зміни функції або прагнення аргументу Х до деякої межі " А " або до. Визначення 1: Нехай функція y=f(х) визначена в деякій...
-
Системи лінійних алгебраїчних рівнянь - Основи вищої математики
1. Будемо розглядати систему з "m" лінійних алгебраїчних рівнянь із "n" невідомими (8.1) Рішенням такої системи називається такий набір чисел Х 1, Х 2,...
-
Визначення : Нехай дана матриця А=(mn), тоді мінором порядку "k" називають визначник, складений з елементів цієї матриці, якщо в неї викреслити (m--k)...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
Матриці. Дії над матрицями Матриця вперше з'явилась в середині ХІХ століття в роботах англійських математиків У. Гамільтона і А. Келі [У. Гамільтон,...
-
Визначники та їх властивості - Основи вищої математики
До поняття визначника приходимо, розглядаючи системи алгебраїчних рівнянь першого степеня. Розглянемо систему рівнянь: (2.1) X та y -- невідомі,...
-
: Елементарна математика, Основні поняття - Основи вищої математики
Основні поняття Визначення. Алгебраїчним виразом називається одна чи декілька алгебраїчних велечин (чисел чи букв) з'єднаних між собою знаками...
-
Застосування потрійних інтегралів до задач геометрії та механіки - Вища математика
1. Потрійний інтеграл в сферичній системі координат. Сферичними координатами точки називаються числа. Де - кут між віссю і радіус-вектором точки ; -...
-
Обчислення потрійних інтегралів в декартових і циліфндричних кординатах - Вища математика
1. Поняття потрійного інтеграла Розглянемо в просторі деяку замкнену область. Нехай в області і на її границі визначена деяка неперервна функія, де -...
-
Досить універсальним методом розв'язку лінійних однорідних систем з сталими коефіцієнтами є матричний метод. Він полягає в наступному. Розглядається...
-
Функції багатьох змінних - Вища математика
Для функції однієї змінної залежна змінна, тобто функція, повністю визначається (залежить) за значенням однієї незалежної змінної. П-1. Об'єм кулі Але...
-
Площа плоскої області обчислюється за формулою (6) У полярній системі координат формула (6) має вигляд (7) Об'єм циліндричного тіла, обмеженою зверху...
-
Обчислення подвійних інтегралів в полярній системі координат - Вища математика
Відомо, що полярні координати довільної точки зв'язані з її декартовими координатами формулами (1) Де Поняття подвійного інтеграла в полярній системі...
-
Границя функції, Неперервність - Вища математика
Нехай функція визначена в деякому околі точки. Околом точки називається сукупність усіх точок таких, що віддаль О-2. (Гепрія Гейне (1821-1881)- нім....
-
Задание №1 Найти матрицу АВ+3Е и ВА+3Е, где , , Е - единичная матрица соответствующего порядка. Решение: Найти матрицу АВ+3Е 1.1 Найдем размер матрицы...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
Пряма на площині. Площина в просторі - Основи вищої математики