:Елементи лінійної алгебри і аналітичної геометрії, Матриці. Дії над матрицями - Основи вищої математики
Матриці. Дії над матрицями
Матриця вперше з'явилась в середині ХІХ століття в роботах англійських математиків У. Гамільтона і А. Келі [У. Гамільтон, 1805-1865, ірландський математик, іноземний член Петербурзької Академії Наук, теорія Комплексних Чисел. Побудував систему чисел -- кватерніонів (чотири).; А. Келі, 1821-1895, англійський математик, іноземний член Петербурзької Академії Наук, праці по теорії і алгебрі, квадратичні формули, проекційна геометрія, математичний аналіз і астрономія], на даний момент широко використовуються в прикладній математиці, вони значно спрощують розгляд складних систем рівнянь.
Визначеня. Матрицею називається прямокутна таблиця, складена з чисел чи функцій. Ми будемо розглядати тільки дійсні числові матриці. Така матриця має вигляд:
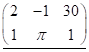
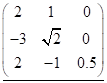
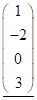
або або або (5) (1.1)
( ) -- знак матриці. В загальному вигляді матриці можна записати наступним чином:
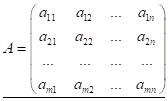
(1.2)
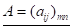
Отже, елемент матриці має два індекси: перший -- номер строки, другий -- стовпця. Можна записати, таким чином
Кожна матриця має певні розміри, тобто кількість рядків і стовпчиків в (1.1) і (1.2) чим і визначається розмір матриці: (2х3), (3х3), (4х1), (1х1), (M X N). При M=n матриця називаєть-ся квадратною, яка має порядок M або N, оскільки вони рівні.
Визначення. Матриця, у якої всі елементи рівні нулю, називається нульовою. Квадрат-на матриця, у якої всі елементи рівні нулю, крім елементів, що стоять на головній діагоналі (яка проходить від верхнього лівого кута у правий нижній кут), називається діагональною і позначається diоg (a, b,...,k). Діагональна матриця, у якої всі діагональні елементи дорівнюють одиниці називається одиничною:
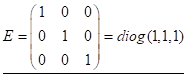
(1.3)
Матриці А і В будуть рівні, якщо однакові розміри і відповідні елементи, тобто.
Матриці одного й того ж розміру, тобто які складаються з однакової кількості рядків і стовпчиків алгебраїчно складають.
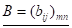
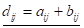
Сумою двох матриць і називається матриця, елементи якої рівні сумі відповідних елементів матриці і, . Символічно це запису-ють (1.4). Виконується закон: (1.5).
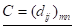
Щоб помножити матрицю А на число, потрібно на це число помножити кожний елемент матриці:
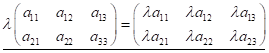
(1.6)
Наслідок: якщо всі елементи матриці мають спільний множник, то його можна виносити за знак матриці.
Визначення. Матриця називається транспонованою, якщо зробити її строки стовпчиками з тими ж самими номерами, тобто
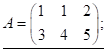
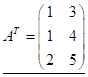
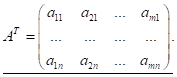
або (1.7)
Властивості транспонованих матриць:
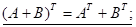
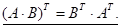
(1.8)
Визначення: Добуток матриць. Дві матриці можна перемножити, якщо число стовпчиків першого множника дорівнює числу строк другого:
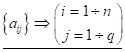
Приклад:
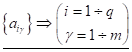
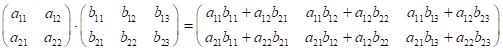
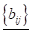
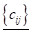
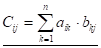
В загальному випадку, якщо якщо ми множимо матрицю розміру M X N на матрицю розміру N x p, ми отримаємо матрицю розміру M x P, елементи якої будуть обчислюватись по формулі: (1.9)
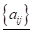
Завжди можна перемножити 2 квадратні матриці одного порядку, в результаті отримаємо квадратну матрицю того ж порядку, тобто можна помножити квадратну матрицю саму на себе, тобто піднести матрицю у квадрат, чого не можна зробити з прямокутною матрицею.
Іншим важливим частковим випадком є множення строчної матриці на стовпчикову, причому ширина першої повинна бути рівна висоті другої, що дає квадратну матрицю першого порядку, тобто число
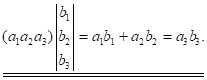
Властивіть добутків матриць:
(1.10)
але!
Похожие статьи
-
Визначення : Нехай дана матриця А=(mn), тоді мінором порядку "k" називають визначник, складений з елементів цієї матриці, якщо в неї викреслити (m--k)...
-
Визначення. Матриця називається оберненою матриці, якщо їх добуток, тобто рівний одиничній матриці. Якщо квадратна матриця має зворотню матрицю, то вона...
-
Визначники та їх властивості - Основи вищої математики
До поняття визначника приходимо, розглядаючи системи алгебраїчних рівнянь першого степеня. Розглянемо систему рівнянь: (2.1) X та y -- невідомі,...
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
Системи лінійних алгебраїчних рівнянь - Основи вищої математики
1. Будемо розглядати систему з "m" лінійних алгебраїчних рівнянь із "n" невідомими (8.1) Рішенням такої системи називається такий набір чисел Х 1, Х 2,...
-
Нескінченно мала й нескінченно велика величини - Основи вищої математики
Визначення . Змінна N , що має межу рівну 0, називається нескінченно малою величиною, якщо для кожного > 0 знайдеться n 0 таке, що | N |< ( N > N 0) ....
-
Вступ, Необхідні відомості з теорії матриць - Невід'ємні матриці
Відомо [[1]-[10]], яку важливу роль відіграють невід'ємні матриці в математичних моделях економіки, біології, теорії ймовірностей тощо. Одними з...
-
І. Визначення : Окружністю називається множина всіх точок площини, що перебувають на однаковій відстані, названій Радіусом , від фіксованої точки,...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ, Поняття межі послідовності - Основи вищої математики
Математика алгебра геометрія тригонометрія Поняття межі послідовності Визначення : Нехай кожному натуральному числу n=1, 2, 3, ... за деяким законом...
-
А) Представлення у вигляді многочлена, тобто можна представити у вигляді многочлена за допомогою елементарних перетворень (приведеня подібних членів і...
-
Теорема 1. Похідна Const =0, тобто якщо Y = С, те Y =0, де С = Const . Y = С -- пряма паралельна осі ОХ й Tg =0, тобто F ( Х) =0. Теорема 2. Постійний...
-
Теореми про межі. Чудові межі - Основи вищої математики
Будемо розглядати сукупність функцій, які залежать від того самого аргументу Х , при цьому Ха або Х . Доведення проводиться для одного із цих випадків,...
-
Розкриття невизначеностей. Формула Тейлора - Основи вищої математики
1. Невизначеність виду 0/0. Теорема 1 ( Правило Лопіталя - Гійом 1661-1704 р., французький математик, автор першого друкованого підручника по...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
Межа функції - Основи вищої математики
Розглянемо деякі випадки зміни функції або прагнення аргументу Х до деякої межі " А " або до. Визначення 1: Нехай функція y=f(х) визначена в деякій...
-
Рівняння, Трансцендентні рівняння - Основи вищої математики
З одним невідомим повинно бути одне, його звичайно приводять до канонічного вигляду: Приклад: Рівняння 1,2,3 ... степені і т. д. -- лінійні рівняння....
-
Вектори. Лінійні операції над векторами, лінійні залежності векторів - Основи вищої математики
Визначення : У фізиці Векторними величинами або Векторами називаються ті, які характеризуються не тільки їхнім числовим значенням, але й напрямком у...
-
Теорема 1. Похідна від функції logax дорівнює, тобто якщо y=logax, то . (11.1) Теорема 2. Похідна від sinx є cosx, тобто якщо y=sinx, то Y =cosx. (11.2)...
-
Пряма в просторі - Основи вищої математики
І. Загальне рівняння прямої Пряму в просторі найчастіше задають як перетинання двох площин І площина А 1 Х + В 1 Y + C 1 Z + D =0 ІІ площина А 2 Х + В 2...
-
Точки розриву і їхня класифікація. Теореми про безперервні функції - Основи вищої математики
Якщо функція F така, що для неї існують межі F ( А +0) і F ( А --0), однак F ( А ) F ( А +0) F ( А --0), то, мабуть, вона нерозривна (не безперервна) у...
-
: Елементарна математика, Основні поняття - Основи вищої математики
Основні поняття Визначення. Алгебраїчним виразом називається одна чи декілька алгебраїчних велечин (чисел чи букв) з'єднаних між собою знаками...
-
Метод Гауса - Основи вищої математики
( Карл Фрідріх Гаус (1777-1855) іноземний член Петербурзької АН (1824), німецький математик. Праці: вища алгебра, диференціальна геометрія, математична...
-
Асимптоти. Вертикальні й горизонтальні - Основи вищої математики
Якщо відстань ОМ від деякої точки О до точки, що Рухається, М, то Відстань О 1 М , на яку Точка М віддаляється від якої-небудь іншої нерухомої Крапки О 1...
-
Дослідження функції однієї змінної за допомогою першої й другої похідних - Основи вищої математики
I. Ознаки сталості зростання й спадання функції Теорема 1. Якщо у всіх точках проміжку A < X < B похідна F ( Х) = 0, то функція F ( Х) зберігає в...
-
LU-розклад матриці, Обчислення власних чисел матриці - Вивчення математичного пакету MathСad
Щоб знайти LU-розклад матриці A, треба використовувати функцію Lu(A) . Функція Lu(A) повертає матрицю, яка містить три квадратні матриці P, L і U,...
-
Безперервність функції - Основи вищої математики
Нехай функція Y = F ( Х) визначена при деякому значенні Х 0 й у деякій околиці із центром у Х 0, нехай Y 0= F ( Х 0). Якщо Х одержить деякий позитивний...
-
Пряма на площині. Площина в просторі - Основи вищої математики
Пряма в просторі І. Пряма на площині 1. Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору Нехай на площині ХО задана точка М...
-
І. Визначення : Мішаним добутком трьох векторів і називається добуток виду, де два перших вектори перемножуються векторно, а їхній добуток множиться...
-
Похідна в економіці - Основи вищої математики
Розглянемо однофакторну або одноресурсну похідну функцію Y = F ( Х) , що дає об'єм виробленої продукції за одиницю часу залежно від об'єму Х витраченого...
-
Матрицы над евклидовым кольцом - Евклидовость в математике
Введем следующее определение: строку над евклидовым кольцом Е будем называть канонической, если, кроме главного элемента, все остальные ее элементы...
-
Теорема Маркова - Невід'ємні матриці
Нехай для стохастичної матриці P існує натуральне число k0 таке, що (тобто всі елементи додатні). Тоді 1. (існування границі матриці означає, що існує...
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Похідна. Її фізична (механічна) і геометрична інтерпретація - Основи вищої математики
І. Вважаючи, що X 0, розглянемо в даній фіксованій точці " Х " відношення приросту функції в цій точці до відповідного приросту аргументу Х . (7.1) (7.1)...
-
Похідна функцій заданих неявно і параметрично - Основи вищої математики
І. Нехай значення двох змінних Х и Y зв'язані між собою деяким рівнянням F ( Х , Y )=0. (13.1) Якщо функція Y = F ( Х) визначена на інтервалі ( А , B )...
-
Границя функції, Неперервність - Вища математика
Нехай функція визначена в деякому околі точки. Околом точки називається сукупність усіх точок таких, що віддаль О-2. (Гепрія Гейне (1821-1881)- нім....
-
Площа плоскої області обчислюється за формулою (6) У полярній системі координат формула (6) має вигляд (7) Об'єм циліндричного тіла, обмеженою зверху...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
:Елементи лінійної алгебри і аналітичної геометрії, Матриці. Дії над матрицями - Основи вищої математики