Оценки интегралов. Формулы среднего значения, Основные правила интегрирования - Определенные интегралы
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда:
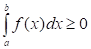
.
2. Если функция интегрируемая на сегменте и, то:
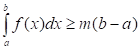
.
3. Если функция непрерывна, неотрицательна и не равна тождественно нулю на сегменте, то:
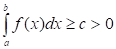
.
Если функции и интегрируемы на сегменте и всюду на этом сегменте, то:
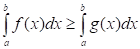
.
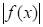
4. Если функция, интегрируемая на сегменте, то и функция также интегрируема на этом сегменте, причем:
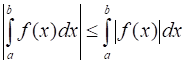
.
5. Пусть функции и интегрируемы на сегменте и. Тогда, если и - точные грани на сегменте, то:
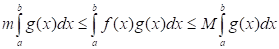
.
6. Пусть функция интегрируема на сегменте, и пусть и - точные грани на сегменте. Тогда найдется такое число, удовлетворяющее неравенствам, что.
Основные правила интегрирования
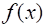
Теорема: Любая непрерывная на интервале функция имеет на этом интервале первообразную. Одной из первообразных является функция:
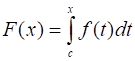
,
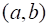
Где - любая фиксированная точка интервала.
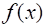
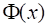
Так как две первообразные данной функции отличаются на постоянную, то согласно теореме, любая первообразная непрерывной на сегменте функции имеет вид:
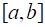
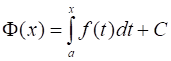
Где - некоторая постоянная.
Полагая в последней формуле сначала, затем, и используя первое свойства определенного интеграла, получим:
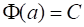
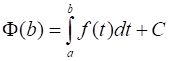
, .
Из этих равенств вытекает соотношение:
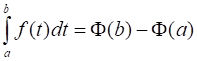
,
Которое называется основной формулой интегрального исчисления или формулой Ньютона - Лейбница.
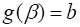
Пусть выполнены следующие условия:
- 1) Функция непрерывна на отрезке ; 2) отрезок является множеством значений некоторой функции, определенной на отрезке и имеющей на этом отрезке непрерывную производную; 3) , .
При этих условиях справедлива формула:
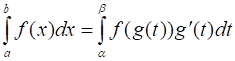
Указанная формула называется формулой замены переменной в определенном интеграле.
Пусть функции и имеют непрерывные производные на сегменте. Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:
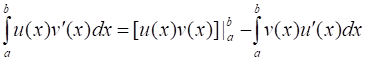
.
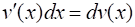
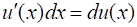
Так как и, то эту формулу можно записать следующим образом:
.
Похожие статьи
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Интегрирование по бесконечному промежутку - Определенные интегралы
Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
-
Определение определенного интеграла - Определенный интеграл
Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл
О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...
-
Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Введение - Определенный интеграл
Мною была выбрана курсовая работа по теме "Определенный интеграл. Приложения определенного интеграла", в связи с этим, я решила узнать, откуда появился...
-
Геометрический смысл определенного интеграла - Неопределенный интеграл
О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Длина дуги кривой - Определенный интеграл
Прямоугольные координаты Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 1). Под длиной...
-
Приложения определенного интеграла. Площадь плоской фигуры - Определенные интегралы
Определение: Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой, при этом кривая называется границей фигуры. Определение: Мы будем...
-
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...
-
Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием: Каждый...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Заключение - Определенный интеграл
Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
Несобственный интеграл. - Неопределенный интеграл
Несобственные интегралы I рода. О: Несобственным интегралом I рода от функции f(x), определенным на множестве [а,?], называется предел, к которому...
-
Основные характеристики нечетких множеств, Примеры нечетких множеств - Нечеткая логика
Пусть M = [0,1] и A - нечеткое множество с элементами из универсального множества E и множеством принадлежностей M - Величина ?A(x) называется...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Метод сравнения является универсальным методом и применяется во всех разделах статистики (метод сравнения средних, оценивания неизвестных параметров и...
-
Таблица 2.10 На 1 января 2008 года В среднем за 2007 год Все население В том числе Всенаселение В том числе Городское Сельское Городское Сельское...
-
Ниже мы постоим парную регрессию, показывающую зависимость от денежной массы. Год Квартал Денежная масса Значение 2003 I 3665,3 330,0 II 4426,5 470,4 III...
-
Площадь поверхности вращения - Определенный интеграл
Пусть кривая АВ Является графиком функции У = f(х) ? 0, где Х [а;b], А функция У = F(х) И ее производная У' = f'(х) Непрерывны на этом отрезке....
-
Объемы тел вращения - Определенные интегралы
Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела. Пусть -...
-
Выявление основной тенденции развития В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления...
-
Возьмем данные об инвестициях в основной капитал (млрд. руб.) Год Квартал Номер квартала Значение 2003 I 1 330 II 2 470,4 III 3 608,8 IV 4 773,7 2004 I 5...
-
Статистики, Свойства оценок - Основы научных исследований
Любая функция от элементов выборки называется Статистикой . Следовательно, точечная оценка также является статистикой. Однако не всякая статистика может...
-
Пусть подынтегральная функция неотрицательна и ограничена: , а двумерная случайная величина распределена равномерно в прямоугольнике D с основанием и...
-
События А и В называются независимыми, если Р(АВ)=Р(А)*Р(В). Пусть например бросаются две монеты; А-выпадение "герба" при первом бросании, В-выпадение...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций
Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
Оценки интегралов. Формулы среднего значения, Основные правила интегрирования - Определенные интегралы