Способ, основанный на истолковании интеграла как площади - Применение метода Монте-Карло в эконометрическом анализе

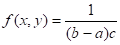
Пусть подынтегральная функция неотрицательна и ограничена: , а двумерная случайная величина распределена равномерно в прямоугольнике D с основанием и высотой. Тогда двумерная плотность вероятности для точек, принадлежащих D; вне D.

В качестве оценки интеграла принимают, где n - общее число случайных точек, принадлежащих D; - число случайных точек, которые расположены под кривой.

Задача. Найти оценку интеграла.

Решение. Используем формулу

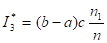
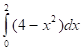
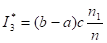
В интервале (0,2) подынтегральная функция неотрицательна и ограничена, причем ; следовательно, можно принять c=4.

Введем в рассмотрение двумерную случайную величину (X, Y), распределенную равномерно в прямоугольнике D с основанием и высотой с=4, плотность вероятности которой

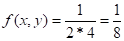
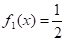
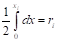
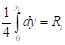
Разыгрываем n=10 случайных точек, принадлежащих прямоугольнику D. Учитывая, что составляющая X в интервале (0,2) распределена равномерно с плотностью и составляющая Y в интервале (0,4) распределена равномерно с плотностью, разыграем координаты случайной точки, принадлежащей прямоугольнику D, по паре независимых случайных чисел : , . Отсюда, .

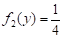
Номер i
1 2 3 4 5 6 7 8 9 10	0,100 0,253 0,520 0,863 0,354 0,809 0,911 0,542 0,056 0,474	0,200 0,506 1,040 1,726 0,708 1,618 1,822 1,084 0,112 0,948	0,040 0,256 1,082 2,979 0,501 2,618 3,320 1,175 0,013 0,899	3,960 3,744 2,918 1,021 3,499 1,382 0,680 2,825 3,987 3,101	0,973 0,376 ,135 0,467 0,876 0,590 0,737 0,048 0,489 0,296	3,892 1,504 0,540 1,868 3,504 2,360 2,948 0,192 1,956 1,184	1 1 1 1 1 1

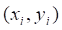
Если окажется, что, то точка лежит под кривой и в "счетчик " надо добавить единицу.

Результаты десяти испытаний приведены в таблице 3.

Из таблицы 3 находим. Искомая оценка интеграла

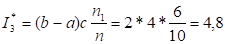
Способ "выделения главной части"

В качестве оценки интеграла принимают

,

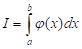
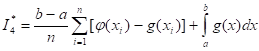
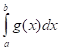
Где - возможные значения случайной величины X, распределенной равномерно в интервале интегрирования, которые разыгрывают по формуле ; функция, причем интеграл можно вычислить обычными методами.

Задача. Найти оценку интеграла.

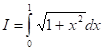
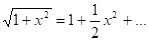
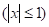
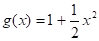
Решение. Так как, то примем. Тогда, полагая число испытаний n=10, имеем оценку

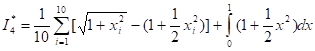
Выполнив элементарные преобразования, получим

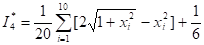
Учитывая, что a=0, b=1, возможные значения разыграем по формуле. Результаты вычислений приведены в таблице 4.

Номер i
1 2 3 4 5 6 7 8 9 10	0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876	0,010 0,947 0,064 0,141 0,270 0,018 0,745 0,218 0,125 0,767	1,010 1,947 1,064 1,141 1,270 1,018 1,745 1,218 1,125 1,767	1,005 1,395 1,032 1,068 1,127 1,009 1,321 1,104 1,061 1,329	2,000 1,843 2,000 1,995 1,984 2,000 1,897 1,990 1,997 1,891

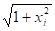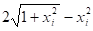
Сложив числа последнего столбца таблицы 4, найдем сумму 19,597, подставив которую в соотношение

,

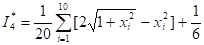
Получим искомую оценку интеграла

.

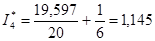
Заметим, что точное значение I=1,147.

Похожие статьи

• Способ существенной выборки, использующий "вспомогательную плотность распределения" - Применение метода Монте-Карло в эконометрическом анализе

  Монте карло погрешность распределение интеграл В качестве оценки интеграла принимают , Где n - число испытаний; F(x) - плотность распределения...

• Способ усреднения подынтегральной функции - Применение метода Монте-Карло в эконометрическом анализе

  В качестве оценки определенного интеграла принимают , Где n - число испытаний; - возможные значения случайной величины X, распределенной равномерно в...

• Программа вычисления определенного интеграла методом Монте-Карло - Применение метода Монте-Карло в эконометрическом анализе

  Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...

• Некоторые сведения теории вероятностей, Математическое ожидание, дисперсия, Точность оценки, доверительная вероятность. Доверительный интервал, Нормальное распределение - Применение метода Монте-Карло в эконометрическом анализе

  Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...

• Метод Монте-Карло, Общая схема метода Монте-Карло, Оценка погрешности метода Монте-Карло - Применение метода Монте-Карло в эконометрическом анализе

  Общая схема метода Монте-Карло Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого...

• Вычисление кратных интегралов методом Монте-Карло - Применение метода Монте-Карло в эконометрическом анализе

  Пусть функция непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл . (1) Геометрически число I представляет собой...

• Введение - Применение метода Монте-Карло в эконометрическом анализе

  Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Возникновение идеи...

• Заключение, Список литературы - Применение метода Монте-Карло в эконометрическом анализе

  Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества: А) Он не требует никаких...

• Вычисление интегралов методом Монте-Карло, Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода - Применение метода Монте-Карло в эконометрическом анализе

  Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...

• Введение, Понятие метода статистического моделирования систем - Моделирование систем массового обслуживания с использованием метода Монте-Карло

  В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно...

• Кубатурная формула типа Симпсона - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага

  Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...

• Разыгрывание противоположных событий, Разыгрывание полной группы событий - Моделирование систем массового обслуживания с использованием метода Монте-Карло

  Пусть требуется разыграть испытания в каждом из которых событие А появляется с вероятностью р и не появляется с вероятностью 1-р [4]. Заменим...

• Предмет метода Монте-Карло, Общая схема метода Монте-Карло - Моделирование систем массового обслуживания с использованием метода Монте-Карло

  Метод Монте-Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для...

• Принципы построения программ с автоматическим выбором шага, Решение задачи, Блок-схема программы, Результаты решения - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага

  При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...

• Нахождение площади поверхности тела вращения, Способ задания функции двух переменных. - Неопределенный интеграл

  Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...

• Метод максимального правдоподобия - Основы научных исследований

  Разработан Р. Фишером. Пусть Х 1 ,х 2 ...х N - выборка из генеральной совокупности случайной величины Х с функцией плотности вероятности Р(х, и),...

• Различные способы формализации экономико-математических и технических систем - Применение экономико-математических методов и моделей в управлении производством (на примере КУП "Спецкоммунтранс")

  Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...

• Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели

  Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...

• Применение статистических методов анализа для адекватной интерпретации результатов контроля остаточных знаний соискателей высшего образования на примере парного t-критерия Стьюдента

  Применение статистических методов анализа для адекватной интерпретации результатов контроля остаточных знаний соискателей высшего образования на примере...

• Адсорбционные методы исследования поверхности - Анализ удельной поверхности активированного угля, основанный на использовании метода тепловой десорбции газа-адсорбата (азота) с поверхности в динамических условиях с помощью специального адсорбера, прибора для текстурных измерений "Термосорб" серии М

  Адсорбционные методы исследования свойств поверхности позволяют количественно охарактеризовать происходящие при адсорбции межмолекулярные взаимодействия,...

• Свойства и области применения углеродных адсорбентов - Анализ удельной поверхности активированного угля, основанный на использовании метода тепловой десорбции газа-адсорбата (азота) с поверхности в динамических условиях с помощью специального адсорбера, прибора для текстурных измерений "Термосорб" серии М

  Попытаемся дать общее представление о свойствах и применении адсорбентов на примере весьма распространенных углеродных материалов. Углеродные адсорбенты...

• Описание качественных и количественных характеристик исходных данных - Имитационное моделирование функционирования отдела планирования и экономического анализа в Могилевском филиале РУП "Белтелеком"

  Целью курсовой работы является эффективная организация работы отдела планирования и экономического анализа Могилевского филиала РУП "Белтелеком"....

• Теоретические методы адсорбции, Модель Ленгмюра - Анализ удельной поверхности активированного угля, основанный на использовании метода тепловой десорбции газа-адсорбата (азота) с поверхности в динамических условиях с помощью специального адсорбера, прибора для текстурных измерений "Термосорб" серии М

  Адсорбция активированный уголь Развитие теории адсорбционных сил еще не достигло такой стадии, когда по известным физико-химическим свойствам газа и...

• Анализ временных рядов, Стационарные временные ряды и их основные характеристики - Динамические ряды

  Стационарные временные ряды и их основные характеристики Поиск модели, адекватно описывающей поведение случайных остатков T анализируемого временного...

• Рисунок. Виды группировок - Метод статистических группировок и его применение в анализе прибыли и ее зависимости от формирующих факторов

  Выбор группировочных признаков всегда должен быть основан на анализе качественной природы исследуемого явления. Всесторонний теоретико-экономический...

• Ранговый метод - Ранговый метод оценивания параметров регрессионной модели

  Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...

• Нелинейное программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

  Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...

• Метод Монте-Карло как разновидность имитационного моделирования - Имитационное моделирование в экономике

  Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием "The Monte Carlo method". Создателями этого метода...

• В чем состоит универсальность метода сравнения и какие направления сравнительно анализа Вам известны?, Раскройте содержание основных правил применения средних в статистических исследованиях - Основы статистики

  Метод сравнения является универсальным методом и применяется во всех разделах статистики (метод сравнения средних, оценивания неизвестных параметров и...

• Основные теоретические сведения - Метод статистических группировок и его применение в анализе прибыли и ее зависимости от формирующих факторов

  В результате первой стадии статистического исследования (статистического наблюдения) получают статистическую информацию, представляющую собой большое...

• Полный факторный эксперимент - Выполнение регрессионного и дисперсионного анализа

  В факторных экспериментах, в отличие от классических, происходит одновременное варьирование всеми независимыми переменными. Эксперимент, в результате...

• Площадь поверхности вращения - Определенный интеграл

  Пусть кривая АВ Является графиком функции У = f(х) ? 0, где Х [а;b], А функция У = F(х) И ее производная У' = f'(х) Непрерывны на этом отрезке....

• Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы

  Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...

• Элементы матричного анализа - Методы решения системы линейных уравнений

  Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...

• Постановка задачи, Понятие о кубатурных формулах, Метод ячеек - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага

  Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...

• Задачи регрессионного анализа, Метод наименьших квадратов - Выполнение регрессионного и дисперсионного анализа

  Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...

• Основные понятия и определения - Анализ удельной поверхности активированного угля, основанный на использовании метода тепловой десорбции газа-адсорбата (азота) с поверхности в динамических условиях с помощью специального адсорбера, прибора для текстурных измерений "Термосорб" серии М

  Описание процессов, происходящих на поверхности, изобилует специальными терминами, и при рассмотрении адсорбционных явлений приходится говорить на языке,...

• Метод решения задачи - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....

• Функции распределения вероятностей для параметров, описываемых обобщенными интервальными оценками - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...

• Метод конечных разностей, Применение для интерполяции/экстраполяции - МАтематическое моделирование в экономике

  Метод конечных разностей -- широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на...

Способ, основанный на истолковании интеграла как площади - Применение метода Монте-Карло в эконометрическом анализе

Предыдущая | Следующая