Непрерывность функции - Свойства функций

Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если

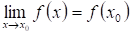
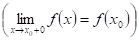
Функция называется Непрерывной слева (справа) в точке, если. Естественно, при этом функция должна быть определена в некоторой окрестности слева (справа) то точки. Непрерывность функции в точке означает непрерывность этой функции в указанной точке как слева, так и справа.

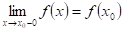
Функция, определенная на интервале называется Непрерывной на интервале , если она непрерывна в каждой точке этого интервала.

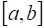
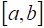
Функция, определенная на отрезке () называется Непрерывной на отрезке , если она непрерывна в каждой точке интервала , непрерывна справа в точке и непрерывна слева в точке.

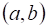
Общие свойства непрерывных функций, заданных на отрезке, определяются четырьмя теоремами: двумя теоремами Больцано-Коши и двумя теоремами Вейерштрасса.

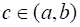
Теорема (первая теорема Больцано-Коши). Пусть функция определена и непрерывна на отрезке , и на концах этого промежутка принимает значения разных знаков; тогда найдется точка , в которой функция равна нулю.

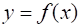
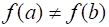
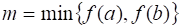
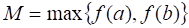
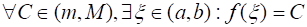
Теорема (вторая теорема Больцано-Коши). Пусть функция определена и непрерывна на отрезке . Тогда, если то функция принимает все свои промежуточные значения, принадлежащие промежутку , где , , т. е. .

Теорема (первая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция является ограниченной на этом отрезке.

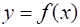
Теорема (вторая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).

Отметим, прежде всего, что основные элементарные функции непрерывны во всех точках, в которых они определены. К основным элементарным функциям относятся:

1. Постоянная функция. Область определения ; 2. Идентичная функция. Область определения ; 3. Одночлен, ; 4. Многочлен, ; 5. Рациональная функция, где и _ многочлены. Функция определена при всех, кроме корней многочлена ; 6. Степенная функция. Если, то функция определена, по крайней мере, на. При определена, по крайней мере, на. (При некоторых степенная функция может быть определена на более широком множестве. Например, функция имеет область определения. Функция определена на ); 7. Показательная функция, , . Определена на ; 8. Логарифмическая функция, , . Определена на ; 9. Синус, косинус определены на. Эти функции являются периодическими с периодом, т. е. , для любого из ; 10. Арксинус и арккосинус определены на.

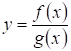
Если и _ непрерывные функции, то их сумма, разность и произведение являются непрерывными функциями. Частное непрерывных функций будет непрерывно всюду, где оно определено. Таким образом, можно утверждать, что всякая арифметическая комбинация непрерывных функций непрерывна всюду, где она определена.

Функция последовательность предел сходимость гейне

Похожие статьи

• Интегрируемость непрерывных, разрывных и монотонных функций, Основные свойства определенного интеграла - Определенные интегралы

  Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...

• Непрерывность композиции, Точки разрыва - Свойства функций

  Пусть задана функция, со значениями в, и на множестве определена функция со значениями в. Тогда для любого можно вычислить, на можно определить функцию...

• ЭКСТРЕМУМ ФУНКЦИИ, ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ - Скалярные и векторные величины, матрицы и функции

  ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ Функция называется Возрастающей на некотором Промежутке , если на этом промежутке большему значению независимой переменной...

• Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений

  Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...

• Бесконечные пределы - Свойства функций

  Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...

• Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций

  Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....

• Свойства числовой функции (четность, нечетность, периодичность), График функции, построение, Смещение графиков вдоль осей ординат, Растяжение графика вдоль оси оу - Математика в современном мире

  Ответ: Функция f называется четной если для любого х из ее области определения f(-x)=f(x) График четной функции симметричен относительно оси ординат....

• Односторонние пределы, Пределы на бесконечности - Свойства функций

  В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...

• ФУНКЦИИ, Основные понятия - Свойства функций

  Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...

• Понятие числовой последовательности - Свойства функций

  Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...

• Тригонометрические функции половинного аргумента, Обратные тригонометрические функции и их свойства, Частные случаи решения тригонометрических уравнений - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...

• Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы

  При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...

• 7. ПРЕДЕЛ ФУНКЦИИ, ПОНЯТИЕ ФУНКЦИИ, ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ - Скалярные и векторные величины, матрицы и функции

  ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...

• О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...

• Основные тригонометрические тождества, Знаки значений тригонометрических функций, Таблица значений, Формулы сложения, Формулы двойного аргумента, Формулы половинного аргумента, Формулы приведения, Формулы синусов и разности синусов (косинусов), График функции у=sinx и его свойства, График функции y=cosx и его свойства, График функции y=tgx и его свойства, График функции y=ctgx и его свойства, Функция y=arcsinx, ее график, свойства - Математика в современном мире

  Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...

• ПРОИЗВОДНАЯ, ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ - Скалярные и векторные величины, матрицы и функции

  ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...

• Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций

  Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....

• Дискретные случайные величины. Распределение случайных величин. Примеры, Функция распределения случайной величины. Свойства. Примеры - Теория вероятности

  Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...

• Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач

  Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...

• О периодических функциях - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....

• Теоремы о пределах, По &;nbsp;теореме&;nbsp; о связи &;nbsp;предела&;nbsp; и бесконечно малой функции: - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...

• НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ ИНФОРМАЦИЯ - Информация, ее виды и свойства

  Чтобы сообщение было передано от источника к получателю, необходима некоторая материальная субстанция - носитель информации. Сообщение, передаваемое с...

• Рекурсивные функции

  Еще одним подходом к проблеме формализации алгоритма являются, так называемые, рекурсивные функции. Исторически этот подход возник первым, поэтому в...

• ДЕЙСТВИЯ НАД ВЕКТОРАМИ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ, РАЗЛОЖЕНИЕ ВЕКТОРА ПО КООРДИНАТНЫМ ОРТАМ, СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ - Скалярные и векторные величины, матрицы и функции

  СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Скалярным произведением двух векторов иназывается число S =|| || сos (). Эта операция обозначается. В частности,...

• Функция y=arccosx, ее график, свойства, Функция y=arctgx, ее график, свойства, Функция y=arcctgx, ее график, свойства, Решение уравнений sinx=a, частные случаи, Решение уравнений cosx=a, частнае случаи, Решение уравнений tgx=a, ctg=a, Решение тригонометрических уравнений, приводимых к квадратным, Решение простейших тригонометрических неравенств, Стереометрия. Основные понятия, обозначения, Аксиомы стереометрии - Математика в современном мире

  Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...

• Бесконечный предел, Замечательные пределы - Свойства функций

  Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно...

• Функции и ее свойства - Методы решения системы линейных уравнений

  В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...

• Логарифмы, Формулы и свойства логарифмов - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...

• Действия над комплексными числами в алгебраической форме, Четность и нечетность функции, Монотонность и периодичность функции, Предел функции в точке - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...

• Синтаксис и семантика. Теорема Райса - Рекурсивные функции

  Попробуем теперь проанализировать круг проблем, неразрешимость которых доказана в предыдущем пункте. Общим для них является то, что по кодам, т. е....

• ПРАВИЛО ЛОПИТАЛЯ - Скалярные и векторные величины, матрицы и функции

  Теорема Коши. Если при соблюдении предположений относительно функций и отношение стремится к некоторому числу при, то тогда к такому же числу будет...

• Функции покупательского спроса. Моделирование и прогнозирование покупательского спроса - Бюджетное множество

  Спрос бюджетный множество потребитель Для индивидуального потребителя может быть сформулирована задача оптимизации выбора. Потребитель, имея доход,...

• Линейная функция - Конформное отображение

  Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...

• Сложная функция, Cхема исследования функции по графику, Тригонометрические функции числового аргумента, Перевод градусной меры угла в радианную и наоборот - Математика в современном мире

  Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...

• Нахождение площади поверхности тела вращения, Способ задания функции двух переменных. - Неопределенный интеграл

  Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...

• Решение квадратных уравнений, Решение квадратных неравенств, Числовая функция и способы ее задания - Математика в современном мире

  Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....

• Интегрирование некоторых классов тригонометрических функций, Определенный интеграл. - Неопределенный интеграл

  Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...

• Интегральная и дифференциальная функции распределения - Основы научных исследований

  Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...

• Необходимое и достаточное условие интегрируемости, Равномерно непрерывные функции - Определенные интегралы

  Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...

• Показательная функция - Конформное отображение

  Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...

Непрерывность функции - Свойства функций

Предыдущая | Следующая