Последовательное интегрирование - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага
Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием:
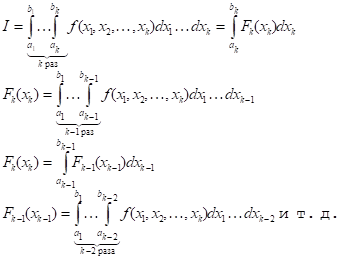
Каждый однократный интеграл легко вычисляется на данной сетке по квадратурным формулам типа:
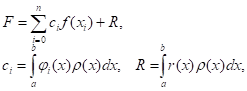
Последовательное интегрирование по всем направлениям приводит к кубатурным формулам, которые являются прямым произведением одномерных квадратурных формул:
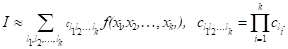
(11)
Например, при K=2, если по каждому направлению выбрана обобщенная формула трапеций, а сетка равномерная, то веса кубатурной формулы равны
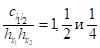
Соответственно для внутренних, граничных и угловых узлов сетки. Легко показать, что для дважды непрерывно дифференцируемых функций эта формула имеет второй порядок точности, и к ней применим метод Рунге-Ромберга.
Вообще говоря, для разных направлений можно использовать квадратурные формулы разных порядков точности
.
Тогда главный член погрешности имеет вид:
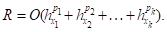
Желательно для всех направлений использовать квадратурные формулы одинакового порядка точности.
Можно подобрать веса и положение линий сетки так, чтобы одномерная квадратурная формула была точна для многочлена максимальной степени, т. е. была бы формулой Гаусса, тогда, для случая K=2:
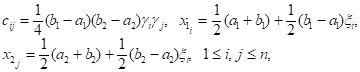
(12)
Где - нули многочленов Лежандра и соответствующие веса. Эти формулы рассчитаны на функции высокой гладкости и дают для них большую экономию в числе узлов по сравнению с более простыми формулами.
Произвольная область. Метод последовательного интегрирования можно применять к области произвольной формы, например, с криволинейной границей. Рассмотрим этот случай при K=2. Для этого проведем через область хорды, параллельные оси, и на них введем узлы, расположенные на каждой хорде так, как нам требуется (рис. 4). Представим интеграл в виде:
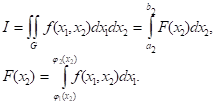
Сначала вычислим интеграл по вдоль каждой хорды по какой-нибудь одномерной квадратурной формуле, используя введенные узлы. Затем вычислим интеграл по ; здесь узлами будут служить проекции хорд на ось ординат.
При вычислении интеграла по имеется одна тонкость. Если область ограничена гладкой кривой, то при
Длина хорды стремится к нулю не линейно, а как
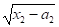
;
Значит, вблизи этой точки
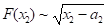
.
То же будет при
.
Поэтому интегрировать непосредственно по формулам высокого порядка точности бессмысленно. Целесообразно выделить из основную особенность в виде веса
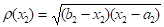
,
Которому соответствуют ортогональные многочлены Чебышева второго рода.
Тогда второе интегрирование выполняется по формулам Гаусса-Кристоффеля:
(13)
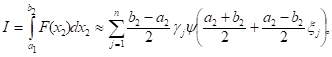
Где, а
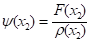
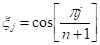
И - нули и веса многочленов Чебышева второго рода.
Чтобы можно было применять эту формулу, надо ординаты хорд на рис. 4 заранее выбрать в соответствии с узлами (13). Если это не было сделано, то придется ограничиться интегрированием по обобщенной формуле трапеций, причем ее эффективный порядок точности в этом случае будет ниже второго.
Похожие статьи
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...
-
Пусть функция непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл . (1) Геометрически число I представляет собой...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Способ усреднения подынтегральной функции - Применение метода Монте-Карло в эконометрическом анализе
В качестве оценки определенного интеграла принимают , Где n - число испытаний; - возможные значения случайной величины X, распределенной равномерно в...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
В зависимости от содержания задачи может быть два случая: когда ребра графа G единичной длины; когда ребра графа произвольной длины. Для каждого из этих...
-
Пусть подынтегральная функция неотрицательна и ограничена: , а двумерная случайная величина распределена равномерно в прямоугольнике D с основанием и...
-
Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Как уже отмечалось социально-экономическое прогнозирование, как и любое прогнозирование вообще, может быть успешным лишь при некоторой стабильности...
-
Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл
О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...
-
МЕТОДЫ ИСКЛЮЧЕНИЯ АВТОКОРРЕЛЯЦИИ ИЗ РЯДОВ ДИНАМИКИ - Основы прогнозирования
Для исключения автокорреляции могут применяться следующие методы: 1. метод конечных разностей; 2. метод исключения тенденций с помощью уравнений...
-
Применительно к предприятию КУП "СПЕЦКОММУНТРАНС" данная задача представляет собой задачу нахождения наилучшего маршрута движения автомобиля,...
-
Геометрический смысл определенного интеграла - Неопределенный интеграл
О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...
-
Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие...
-
Определение определенного интеграла - Определенный интеграл
Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...
-
Модель Лефевра-Николиса описывает колебательные процессы в следующей цепочке химических реакций: Предполагается, что концентрации веществ A, B, D, E...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
-
Статистические испытания схемы проводятся исходя из того, что генерирование случайных логических переменных xI проводится с помощью равномерного...
-
Пусть в пространстве дано тело, ограниченное некоторой замкнутой поверхностью и пусть известна площадь любого его сечения, полученного плоскость,...
-
Выбор метода производства (или выделение) готового продукта Современные методы производства азотной кислоты основаны на применении синтетического аммиака...
-
В аналитической части изложены результаты проведенного исследования основных показателей доходов и уровня жизни населения в регионах Российской Федерации...
-
Методы вычисления определителей
Вычислить сумму матриц kA+mB, если, Вычисление линейный уравнение Вычислить определитель третьего порядка: Решить систему линейных уравнений методом...
-
Проблема прогнозирования вероятности банкротства существует уже несколько десятков лет - все началось с работ Ramser, Foster (1931), Fitzpatrick (1932) и...
-
Неопределенность - это фундаментальное свойство природы, а еще более (и точнее) - свойство, характеризующее неточность, незамкнутость, неокончательность,...
-
Интегрирование по бесконечному промежутку - Определенные интегралы
Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Итак, модели, которые будут дальше анализироваться, и получены с помощью Первого метода - проведения теста для выделения наиболее дескриптивных...
Последовательное интегрирование - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага