ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы
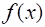
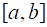
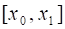
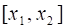
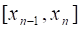
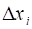
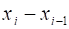
Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на частичных сегментов, , , . Точки, , , будем называть точками разбиения. Пусть - произвольная точка частичного сегмента, а - разность, которую мы в дальнейшем будем называть длиной частичного сегмента.
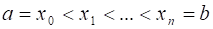
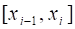
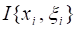
Определение. Число, где:
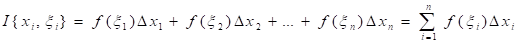
Называется Интегральной суммой (или суммой Римана) функции, соответствующей разбиению сегмента и данному выбору промежуточных точек на частичных сегментах.
Геометрический смысл интегральной суммы - площадь ступенчатой фигуры.
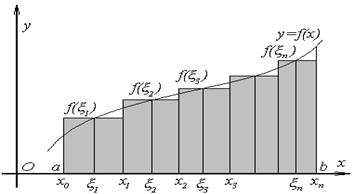
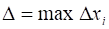
Введем обозначение.
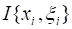
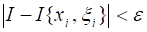
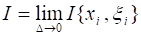
Определение. Число называется Пределом интегральных сумм при, если для любого положительного можно указать такое число, что для любого разбиения сегмента, для которого максимальная длина частичных сегментов меньше, независимо от выбора точек, на сегментах выполняется неравенство
, т. е. .
Определение.: Функция называется Интегрируемой (по Риману) на сегменте, если существует конечный предел интегральных сумм этой функции при. Указанный предел называется Определенным интегралом функции по сегменту и обозначается следующим образом:
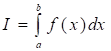
.
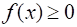
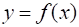
Числа и называются, соответственно, верхним и нижним пределом интегрирования, а отрезок - интервалом интегрирования. В случае определенный интеграл равен площади криволинейной трапеции, границами которой являются: ось, линии и, а также график функции. Обозначим через и соответственно точную верхнюю и точную нижнюю грани этой функции на сегменте.
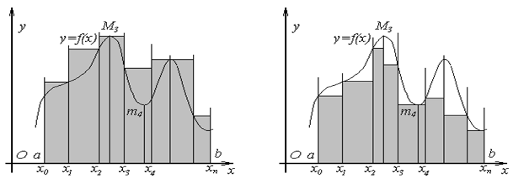
Определение: Суммы:
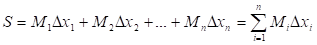
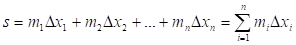
Называют соответственно верхней и нижней суммами Дарбу функции для данного разбиения сегмента.
Очевидно, что любая интегральная сумма данного разбиения сегмента заключена между верхней и нижней суммой и этого разбиения.
Свойства верхних и нижних сумм:
- 1. Для любого фиксированного разбиения и для любого промежуточные точки на сегментах можно выбрать так, что интегральная сумма будет удовлетворять неравенствам. Точки на сегментах можно выбрать также и таким образом, что интегральная сумма будет удовлетворять неравенствам. 2. Если разбиение сегмента получено путем добавления новых точек к точкам разбиения этого сегмента, то для верхних и нижних сумм этих разбиений выполнены неравенства и. 3. Пусть и - любые два разбиения сегмента. Тогда если, и, - соответственно нижние и верхние суммы разбиений и, то и. 4. Множество верхних сумм данной функции для всевозможных разбиений сегмента ограничено снизу. Множество нижних сумм ограничено сверху.
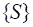
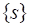
Обозначим через точную нижнюю грань множества верхних сумм, а через - точную верхнюю грань множества нижних сумм.
Определение: Числа и называются соответственно верхним и нижним интегралами Дарбу от функции.
- 5. Пусть разбиение сегмента получено из разбиения добавлением к последнему новых точек, и пусть, если, и, - соответственно нижние и верхние суммы разбиений и. Тогда для разностей и может быть получена оценка, зависящая от максимальной длины частичных сегментов разбиения, числа добавленных точек и точных верхней и нижней граней и функции на сегменте. Именно и. 6. Лемма Дарбу: Верхний и нижний интеграл Дарбу и от функции по сегменту являются соответственно пределами верхних и нижних сумм при и, следовательно, :
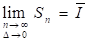
, , и при этом.
Похожие статьи
-
Приложения определенного интеграла. Площадь плоской фигуры - Определенные интегралы
Определение: Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой, при этом кривая называется границей фигуры. Определение: Мы будем...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Определение определенного интеграла - Определенный интеграл
Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
Объемы тел вращения - Определенные интегралы
Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела. Пусть -...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
Интегрирование по бесконечному промежутку - Определенные интегралы
Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...
-
Длина дуги кривой - Определенный интеграл
Прямоугольные координаты Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 1). Под длиной...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Геометрический смысл определенного интеграла - Неопределенный интеграл
О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...
-
Заключение - Определенный интеграл
Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Введение - Определенный интеграл
Мною была выбрана курсовая работа по теме "Определенный интеграл. Приложения определенного интеграла", в связи с этим, я решила узнать, откуда появился...
-
Площадь поверхности вращения - Определенный интеграл
Пусть кривая АВ Является графиком функции У = f(х) ? 0, где Х [а;b], А функция У = F(х) И ее производная У' = f'(х) Непрерывны на этом отрезке....
-
Симплекс - метод - Интегральное и дифференциальное исчисление
Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Литература: - Определенный интеграл
Интеграл лагранж функция коши 1. Виленкин М. Я., О. С. Ивашев - Мусатов, С. И. Шварцбурд, "Алгебра и математический анализ", Москва,1993г. 2. Власов В....
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Несобственный интеграл. - Неопределенный интеграл
Несобственные интегралы I рода. О: Несобственным интегралом I рода от функции f(x), определенным на множестве [а,?], называется предел, к которому...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Интегральная теорема Муавра-Лапласа
Предположим, что в условиях схемы Бернулли проводится испытаний, в результате каждого из которых с вероятностью () происходит событие. Интегральная...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Пусть в пространстве дано тело, ограниченное некоторой замкнутой поверхностью и пусть известна площадь любого его сечения, полученного плоскость,...
-
Гомоскедастичностью называется выполняемость предпосылки о постоянстве дисперсии отклонений. Гетероскедастичностью называется невыполняемость этой самой...
-
Пусть функция непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл . (1) Геометрически число I представляет собой...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Теоремы Ферма, Ролля, Лагранжа и Коши
Введение В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл
О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Дифференциальные уравнения - Неопределенный интеграл
Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы