Интегрируемость непрерывных, разрывных и монотонных функций, Основные свойства определенного интеграла - Определенные интегралы

Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте.

Теорема: Если функция определена и ограничена на сегменте, и если для любого числа можно указать конечное число интервалов, покрывающих все точки разрыва этой функции и имеющих общую длину меньше, то интегрируема на сегменте.

Следствие: Ограниченная на сегменте функция, имеющая лишь конечное число точек разрыва первого рода, интегрируема на этом сегменте. В частности, кусочно-непрерывная на данном сегменте функция интегрируема на этом сегменте.

Теорема: Монотонная на сегменте функция интегрируема на этом сегменте.

Основные свойства определенного интеграла

1. Будем считать, что определенный интеграл с одинаковыми пределами интегрирования равен нулю (по определению):

.

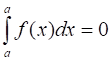
2. Будем считать, что при перемене мест верхнего и нижнего пределов интегрирования определенный интеграл меняет знак на противоположный:

.

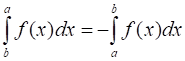
3. Пусть функции и интегрируемы на сегменте, тогда функции, и также интегрируемы на этом сегменте, причем:

.

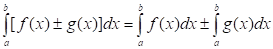
4. Если функция интегрируема на сегменте, то функция (=const) интегрируема на этом сегменте, причем:

.

5. Если функция интегрируема на сегменте, то эта функция интегрируема на любом сегменте, содержащемся в сегменте. 6. Пусть функция интегрируема на сегментах и. Тогда эта функция интегрируема на сегменте, причем:

.

Похожие статьи

• Оценки интегралов. Формулы среднего значения, Основные правила интегрирования - Определенные интегралы

  1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...

• Необходимое и достаточное условие интегрируемости, Равномерно непрерывные функции - Определенные интегралы

  Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...

• Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы

  При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...

• Определение определенного интеграла - Определенный интеграл

  Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...

• Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций

  Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....

• Геометрический смысл определенного интеграла - Неопределенный интеграл

  О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...

• ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы

  Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...

• Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций

  Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....

• Приложения определенного интеграла. Площадь плоской фигуры - Определенные интегралы

  Определение: Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой, при этом кривая называется границей фигуры. Определение: Мы будем...

• Непрерывность функции - Свойства функций

  Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...

• Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл

  О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...

• Площадь криволинейной трапеции - Определенный интеграл

  Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...

• ФУНКЦИИ, Основные понятия - Свойства функций

  Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...

• Бесконечные пределы - Свойства функций

  Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...

• Теоремы о пределах, По &;nbsp;теореме&;nbsp; о связи &;nbsp;предела&;nbsp; и бесконечно малой функции: - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...

• Интегрирование по бесконечному промежутку - Определенные интегралы

  Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...

• Непрерывность композиции, Точки разрыва - Свойства функций

  Пусть задана функция, со значениями в, и на множестве определена функция со значениями в. Тогда для любого можно вычислить, на можно определить функцию...

• Интегрирование некоторых классов тригонометрических функций, Определенный интеграл. - Неопределенный интеграл

  Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...

• Объемы тел вращения - Определенные интегралы

  Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела. Пусть -...

• 7. ПРЕДЕЛ ФУНКЦИИ, ПОНЯТИЕ ФУНКЦИИ, ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ - Скалярные и векторные величины, матрицы и функции

  ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...

• Понятие числовой последовательности - Свойства функций

  Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...

• Несобственный интеграл. - Неопределенный интеграл

  Несобственные интегралы I рода. О: Несобственным интегралом I рода от функции f(x), определенным на множестве [а,?], называется предел, к которому...

• Заключение - Определенный интеграл

  Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...

• Основные тригонометрические тождества, Знаки значений тригонометрических функций, Таблица значений, Формулы сложения, Формулы двойного аргумента, Формулы половинного аргумента, Формулы приведения, Формулы синусов и разности синусов (косинусов), График функции у=sinx и его свойства, График функции y=cosx и его свойства, График функции y=tgx и его свойства, График функции y=ctgx и его свойства, Функция y=arcsinx, ее график, свойства - Математика в современном мире

  Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...

• Односторонние пределы, Пределы на бесконечности - Свойства функций

  В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...

• Функции и ее свойства - Методы решения системы линейных уравнений

  В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...

• Введение - Определенный интеграл

  Мною была выбрана курсовая работа по теме "Определенный интеграл. Приложения определенного интеграла", в связи с этим, я решила узнать, откуда появился...

• Программа вычисления определенного интеграла методом Монте-Карло - Применение метода Монте-Карло в эконометрическом анализе

  Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...

• Длина дуги кривой - Определенный интеграл

  Прямоугольные координаты Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 1). Под длиной...

• Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач

  Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...

• Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы

  Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...

• Функция y=arccosx, ее график, свойства, Функция y=arctgx, ее график, свойства, Функция y=arcctgx, ее график, свойства, Решение уравнений sinx=a, частные случаи, Решение уравнений cosx=a, частнае случаи, Решение уравнений tgx=a, ctg=a, Решение тригонометрических уравнений, приводимых к квадратным, Решение простейших тригонометрических неравенств, Стереометрия. Основные понятия, обозначения, Аксиомы стереометрии - Математика в современном мире

  Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...

• Нахождение площади поверхности тела вращения, Способ задания функции двух переменных. - Неопределенный интеграл

  Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...

• Свойства числовой функции (четность, нечетность, периодичность), График функции, построение, Смещение графиков вдоль осей ординат, Растяжение графика вдоль оси оу - Математика в современном мире

  Ответ: Функция f называется четной если для любого х из ее области определения f(-x)=f(x) График четной функции симметричен относительно оси ординат....

• Действия над комплексными числами в алгебраической форме, Четность и нечетность функции, Монотонность и периодичность функции, Предел функции в точке - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...

• Способ усреднения подынтегральной функции - Применение метода Монте-Карло в эконометрическом анализе

  В качестве оценки определенного интеграла принимают , Где n - число испытаний; - возможные значения случайной величины X, распределенной равномерно в...

• Вычисление объема тела п площади параллельных плоскостных сечений. Вычисление объема тела вращения - Неопределенный интеграл

  Пусть в пространстве дано тело, ограниченное некоторой замкнутой поверхностью и пусть известна площадь любого его сечения, полученного плоскость,...

• ПРАВИЛО ЛОПИТАЛЯ - Скалярные и векторные величины, матрицы и функции

  Теорема Коши. Если при соблюдении предположений относительно функций и отношение стремится к некоторому числу при, то тогда к такому же числу будет...

• ПРОИЗВОДНАЯ, ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ - Скалярные и векторные величины, матрицы и функции

  ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...

• Линейная функция - Конформное отображение

  Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...

Интегрируемость непрерывных, разрывных и монотонных функций, Основные свойства определенного интеграла - Определенные интегралы

Предыдущая | Следующая