Определение определенного интеграла - Определенный интеграл
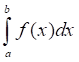
Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
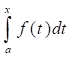
Обозначим = f(х). Найдем производную функции f(х) по переменному верхнему пределу х.
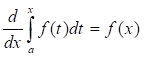
Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема 1: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема 2: (Теорема Ньютона - Лейбница)
Если функция F(x) - какая - либо первообразная от непрерывной функции f(x), то:
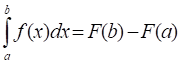
Это выражение известно под названием формулы Ньютона - Лейбница.
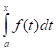
Доказательство: Пусть F(x) - первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция - первообразная функция от f(x). Но т. к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое - то постоянное число С, то
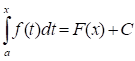
При соответствующем выборе С это равенство справедливо для любого х, т. е. при х = а:
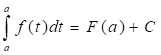
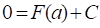
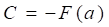
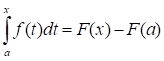
Тогда.
А при х = b:

Заменив переменную t на переменную х, получаем формулу Ньютона - Лейбница:
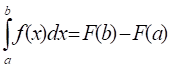
Теорема доказана.
Иногда применяют обозначение F(b) - F(a) = F(x).
Формула Ньютона - Лейбница представляет собой общий подход к нахождению определенных интегралов.
Определение. Если существует конечный передел интегральной суммы (1)
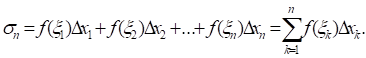
При ?>0, не зависящий от способа разбиения ?N отрезка [a; b] на частичные отрезки и выбора промежуточных точек ?K, то этот предел называют определенным интегралом (или интегралом Римана) от функции f(x) на отрезке [a; b] и обозначают:
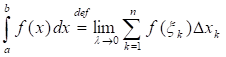
Если указанный предел существует, то функция f(x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману). При этом f(x)dx называется подынтегральным выражением, f(x) - подынтегральной функцией, х - переменной интегрирования, a и b - соответственно нижним и верхним пределами интегрирования.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения ? стремится к нулю.
Условия существования определенного интеграла
1) Интегрируемая функция необходимо ограничена.
Если бы функция f(x) была в промежутке [a, b] неограниченна, то - при любом разбиении промежутка на части - она сохранила бы подобное свойство хоть в одной из частей. Тогда за счет выбора в этой части точки можно было бы сделать f(), а с ней и сумму, - сколь угодно большой; при этих условиях конечного предела для существовать не могло бы.
- 2) Для существования определенного интеграла необходимо и достаточно, чтобы было (S - s) = 0 S = m ?X, S = M ?X,
Где m и M - точные нижняя и верхняя грани. Суммы Дарбу s и S служат точными, соответственно, нижней и верхней границами для интегральных сумм.[6]
Основные свойства определенного интеграла:
1. Если нижний и верхний пределы интегрирования равны (a=b), то интеграл равен нулю:
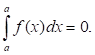
Это свойство следует из определения интеграла.
2. Если f(x)=1, то
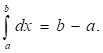
Действительно, так как f(x)=1, то
- 3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный: 4. Постоянный множитель можно выносить за знак определенного интеграла:
R
- 5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1(x), f2(x), ..., fN(x) равен алгебраической сумме определенных интегралов от слагаемых: 6. (аддитивность определенного интеграла). Если существуют интегралы и то существует также интеграл и для любых чисел a, b, c; 7. Если f(x) ? 0 [a; b], то
a < b
8 . (определенность определенного интеграла). Если интегрируемые функции f(x) и ?(x) удовлетворяют неравенству f(x) ? ?(x) [a; b], то
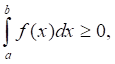
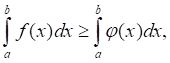
a >b.
9 . (об оценке определенного интеграла). Если m и М - соответственно наименьшее и наибольшее значения функции f(x), непрерывной на отрезке [a; b], то
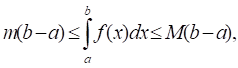
a < b.
10. (теорема о среднем). Если функция f(x) непрерывна на отрезке [a; b], то существует такая точка [a; b], что
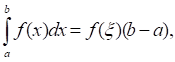
Т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ? отрезка интегрирования [a; b] и длины B-a этого отрезка.[10]
1.
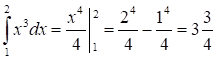
.
Пример 2.
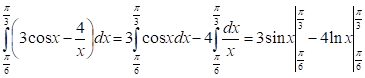
Похожие статьи
-
Геометрический смысл определенного интеграла - Неопределенный интеграл
О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Интегрирование по бесконечному промежутку - Определенные интегралы
Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...
-
Заключение - Определенный интеграл
Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...
-
Введение - Определенный интеграл
Мною была выбрана курсовая работа по теме "Определенный интеграл. Приложения определенного интеграла", в связи с этим, я решила узнать, откуда появился...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Объемы тел вращения - Определенные интегралы
Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела. Пусть -...
-
Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
Длина дуги кривой - Определенный интеграл
Прямоугольные координаты Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 1). Под длиной...
-
Приложения определенного интеграла. Площадь плоской фигуры - Определенные интегралы
Определение: Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой, при этом кривая называется границей фигуры. Определение: Мы будем...
-
Литература: - Определенный интеграл
Интеграл лагранж функция коши 1. Виленкин М. Я., О. С. Ивашев - Мусатов, С. И. Шварцбурд, "Алгебра и математический анализ", Москва,1993г. 2. Власов В....
-
Площадь поверхности вращения - Определенный интеграл
Пусть кривая АВ Является графиком функции У = f(х) ? 0, где Х [а;b], А функция У = F(х) И ее производная У' = f'(х) Непрерывны на этом отрезке....
-
Определяли динамическую обменную емкость, полную динамическую обменную емкость и степень отмывки смолы КУ-2 от Cu2+-катионов 5% раствором серной кислоты....
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Несобственный интеграл. - Неопределенный интеграл
Несобственные интегралы I рода. О: Несобственным интегралом I рода от функции f(x), определенным на множестве [а,?], называется предел, к которому...
-
Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл
О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...
-
Определение скорости пара и диаметра колонны - Колонные аппараты
Средние массовые расходы (нагрузки) по жидкости для верхней и нижней частей колонны определяют из соотношений: Где МD и МF - мольные массы дистиллята...
-
Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием: Каждый...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Модель с определением точки заказа - Экономико-математические модели управления запасами
В реальных ситуациях следует учитывать время выполнения заказа Q. Для обеспечения бесперебойного снабжения заказ должен подаваться в момент, когда...
-
Дифференциальные уравнения - Неопределенный интеграл
Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Определение числа тарелок - Колонные аппараты
Для определения числа тарелок воспользуемся методом кинетической кривой. Этот метод основан на определении КПД тарелки по Мэрфи и позволяет находить...
-
Пусть необходимо подобрать оптимальные настройки для объекта с передаточной функцией (9). Степень затухания, к примеру, ш= 0.75. Ниже даются рекомендации...
-
Определение необходимого объема выборки - Основы эконометрики
В практике проектирования выборочного наблюдения возникает вопрос о необходимой численности выборки, которая необходима для обеспечения определенной...
-
Скорость падения дождевых капель на определенный предмет
Введение Математика, как наука родилась тысячи лет назад, ибо человек всегда старался познать мир. Эти знания были необходимы древним купцам и...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
Определение. Примеры - Формационные основы универсальных алгебр
1. Пусть А - непустое множество (АШ), n -- натуральное число, - декартова (прямая) n-ая степень множества А. В частности, если n=0, то под будем понимать...
-
Односторонние пределы, Пределы на бесконечности - Свойства функций
В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...
-
Основные понятия и определения проблемы прогнозирования - Прогнозирующие системы
Необходимо отметить, что мы рассматриваем прогнозирование в целях планирования производства или управления запасами. Таким образом, наш интерес лежит в...
Определение определенного интеграла - Определенный интеграл