Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций
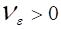
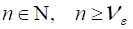
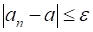
Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: .
Число называют Пределом последовательности . При этом записывают или.
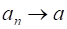
Пример. .
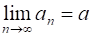
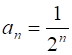
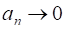
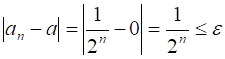
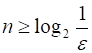
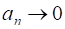
Покажем, что . Зададим любое число . Неравенство выполняется для , такого, что , что определение сходимости выполняется для числа . Значит, .
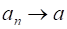
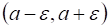
Иными словами означает, что все члены последовательности с достаточно большими номерами мало отличается от числа, т. е. начиная с некоторого номера (при ) элементы последовательности находятся в интервале, который называется - окрестностью точки.
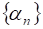
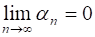
Последовательность, предел которой равен нулю (, или при ) называется Бесконечно малой.
Применительно к бесконечно малым справедливы утверждения:
- - Сумма двух бесконечно малых является бесконечно малой; - Произведение бесконечно малой на ограниченную величину является бесконечно малой.
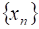
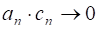
Теорема. Для того чтобы последовательность имела предел, необходимо и достаточно чтобы , где - постоянная; - бесконечно малая.
Основные свойства сходящихся последовательностей:
- 1. Сходящаяся последовательность имеет только один предел; 2. Сходящаяся последовательность ограничена; 3. Если, то ; 4. При любых постоянных и ; 5. ; 6. Если, и, то ; 7. Если, то ; 8. Если и, то ; 9. Если, то.
Свойства 3. и 4. обобщаются на случай любого числа сходящихся последовательностей.
Отметим, что при вычислении предела дроби, числитель и знаменатель которой представляют собой линейные комбинации степеней, предел дроби равен пределу отношения старших членов (т. е. членов, содержащих наибольшие степени числителя и знаменателя).
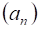
Последовательность называется:
Возрастающей, если ;
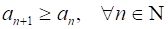
Строго возрастающей, если ;
Убывающей, если ;
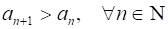
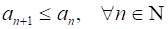
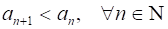
Строго убывающей, если.
Все такие последовательности называют Монотонными.
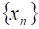
Теорема. Если последовательность монотонно возрастает и ограничена сверху, то она сходится и ее предел равен ее точной верхней грани; если последовательность убывает и ограничена снизу, то она сходится к своей точной нижней грани.
Похожие статьи
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Понятие числовой последовательности - Свойства функций
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Бесконечные пределы - Свойства функций
Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Бесконечный предел, Замечательные пределы - Свойства функций
Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...
-
Ответ: Функция f называется четной если для любого х из ее области определения f(-x)=f(x) График четной функции симметричен относительно оси ординат....
-
Односторонние пределы, Пределы на бесконечности - Свойства функций
В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Теория алгоритмов. Основные результаты, Программы как данные - Рекурсивные функции
Вместо предисловия . Сверх-идеей любой научной теории можно считать перевод знания из сферы подсознательного, интуитивногов осознанную, точную и...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СКАЛЯРНЫХ И ВЕКТОРНЫХ ВЕЛИЧИН Величины называют Скалярными (скалярами), Если они после выбора единиц измерения полностью...
-
Непрерывность композиции, Точки разрыва - Свойства функций
Пусть задана функция, со значениями в, и на множестве определена функция со значениями в. Тогда для любого можно вычислить, на можно определить функцию...
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Свойство 1. Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания...
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
-
Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
Кислород: история открытия и основные свойства
Кислород - элемент главной подгруппы шестой группы, второго периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 8....
-
Еще одним подходом к проблеме формализации алгоритма являются, так называемые, рекурсивные функции. Исторически этот подход возник первым, поэтому в...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Скалярным произведением двух векторов иназывается число S =|| || сos (). Эта операция обозначается. В частности,...
-
Применение Промышленное производство винилхлорида входит в первую десятку производства крупнейших многотонажных продуктов основного органического...
-
Медицина - Серебро: основные свойства и роль в мировой культуре
Одной из важных сфер использования серебра являлась алхимия, тесно связанная с медициной. Уже за 3 тыс. лет до н. э. в Китае, Персии и Египте были...
-
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины. Матрицы равны между собой, если равны все их соответствующие...
-
Электротехника и ювелирное дело Так как обладает наибольшей электропроводностью, теплопроводностью и стойкостью к окислению кислородом при обычных...
-
Физиологическое действие - Серебро: основные свойства и роль в мировой культуре
Обычно серебро поступает в организм с водой и пищей в ничтожно малых количествах -- всего 7 микрограммов в сутки. И при этом такое явление, как дефицит...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
Технологический процесс изготовле-ния бумаги (картона) включает следующие основные операции: Аккумулирование бумажной массы; разбавление ее водой до...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Лемма (о декартовом произведении)., Замечания и упражнения - Рекурсивные функции
Если А - эффективное множество, то Для любого эффективного множества B AB эффективно (и, следовательно, любое декартово произведение A1A2...Аn...
-
В настоящее время из всех полупроводниковых материалов наибольшее применение для изготовления полупроводниковых ИМС получил кремний. Кремний - элемент IV...
-
На уровне общества для описания поведения потребителей вводится целевая функция потребления. Целевая функция потребления - функция, выражающая уровень...
Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций