Геометрический смысл определенного интеграла - Неопределенный интеграл
О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс - нижним основанием.
Теорема существования определенного интеграла
Т: Если функция f(x) непрерывна на отрезке АВ, то ее интегральная сумма стремится к пределу при неограниченном увеличении числа точек разбиения и стремящейся к нулю длины наибольшего отрезка разбиения, не зависит от способа разбиения отрезка АВ на частичные отрезки и выбора в них промежутка точки.
Свойства определенного интеграла.
1. Определенный интеграл от суммы конечного числа функций равен сумме интегралов от подынтегральных функций.
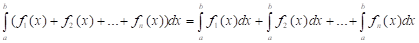
Д:
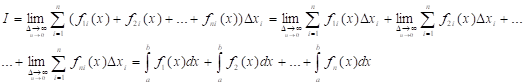
2. Постоянный множитель можно выносить за знак определенного интеграла.
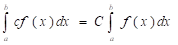
Д:
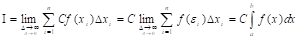
3. Если поменять местами пределы интегрирования, то знак перед интегралом поменяется на противоположный.
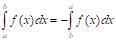
Д:
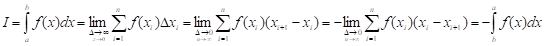
4. Если отрезок интегрирования [a, b] разбить на две части точкой С так, что [a, b]=[a, c]+[c, b], то
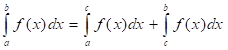
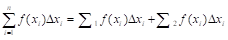
Д: Так как предел интегральной суммы не зависит от способа разбиения отрезка [a, b] на частичные отрезки, выберем точку С таким образом, чтобы она совпадала с одной из точек разбиения. Тогда, (1), где первая сумма правой части функции
(1) - сумма, соответствующая точкам разбиения отрезка [a, c], а вторая - отрезку [c, b],
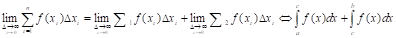
С: Если С1, С2,... СNЄ [a, b], то
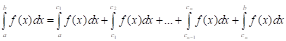
5. Если подынтегральная функция на отрезке [a, b] не меняет знак, то интеграл является числом такого же знака, что и подынтегральная функция на отрезке интегрирования [a, b], т. е., если f(x)?0, хє [a, b] =>
Д:
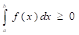
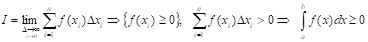
6. Значение определенного интеграла находится между произведением наименьшего и наибольшего значения подынтегральной функции на длину отрезка интегрирования, т. е.
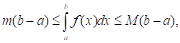
Где.
Д:
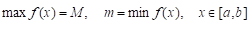
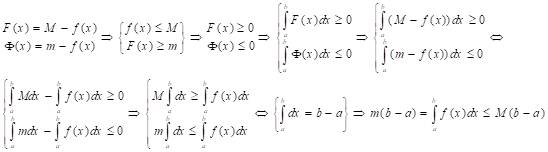
7. Если то интеграл
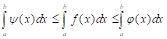
Д:
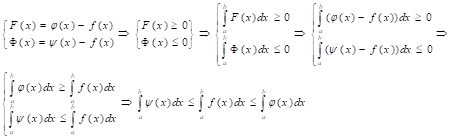
8. Теорема о среднем.
Т: Внутри отрезка [a, b] существует хотя бы одно значение х=еє [a, b], такое что:
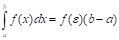
Д: Пусть, тогда ;
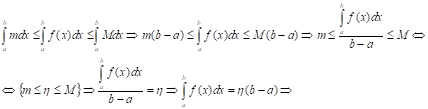
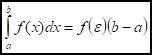
- Теорема о среднем для определения интеграла.
9. Формула для вычисления производной от определенного интеграла по переменному верхнему пределу.
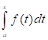
Д:
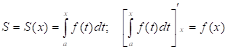
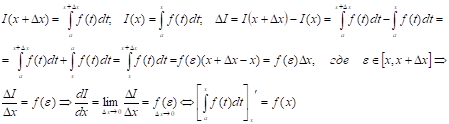
10. Формула Ньютона - Лейбница.
О: Значение определенного интеграла равняется разности значений любой первообразной для подынтегральной функции в точках верхнего и нижнего предела соответственно, т. е.
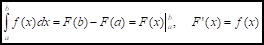
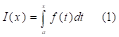
Д: Рассмотрим интеграл.
Из функции (1) следует, что I(x) является первообразной для подынтегральной функции f(x), т. к. I' (x)= f(x). Пусть F(x) - какая-то первообразная для подынтегральной функции, тогда I(x)=F(x)+c (2).
Из (1) =>
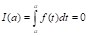
Из (2) =>
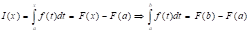
Замена переменной в определенном интеграле
Т: Если на отрезке [х1,Х2] функции непрерывны и, то интеграл от
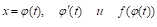
Д:
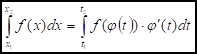
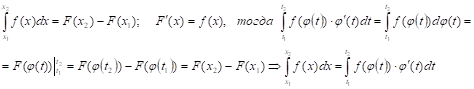
Интегрирование по частям в определенном интеграле.
Т: Пусть U=U(x), V=V(x), тогда
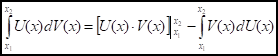
Д: Т. к. определенный интеграл равен разности значений первообразной в точках верхнего и нижнего и верхнего пределов, то интеграл
Похожие статьи
-
Определение определенного интеграла - Определенный интеграл
Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Несобственный интеграл. - Неопределенный интеграл
Несобственные интегралы I рода. О: Несобственным интегралом I рода от функции f(x), определенным на множестве [а,?], называется предел, к которому...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
-
Неопределенный интеграл, Свойства неопределенных интегралов - Неопределенный интеграл
О: Первообразной от функции y=f(x) называется функция F(x), такая что F' (x)=f(x) Т: Всякая непрерывная функция y=f(x) имеет бесконечное множество...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...
-
Приложения определенного интеграла. Площадь плоской фигуры - Определенные интегралы
Определение: Плоская фигура - часть плоскости, ограниченная простой замкнутой кривой, при этом кривая называется границей фигуры. Определение: Мы будем...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Пусть в пространстве дано тело, ограниченное некоторой замкнутой поверхностью и пусть известна площадь любого его сечения, полученного плоскость,...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Интегрирование по бесконечному промежутку - Определенные интегралы
Определение: Пусть функция интегрируема на каждом отрезке, т. е. существует определенный интеграл. Тогда за несобственный интеграл принимают предел. Если...
-
Дифференциальные уравнения - Неопределенный интеграл
Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...
-
Пусть подынтегральная функция неотрицательна и ограничена: , а двумерная случайная величина распределена равномерно в прямоугольнике D с основанием и...
-
Объемы тел вращения - Определенные интегралы
Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела. Пусть -...
-
Заключение - Определенный интеграл
Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...
-
Введение - Определенный интеграл
Мною была выбрана курсовая работа по теме "Определенный интеграл. Приложения определенного интеграла", в связи с этим, я решила узнать, откуда появился...
-
Квантиль - Это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...
-
Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием: Каждый...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Длина дуги кривой - Определенный интеграл
Прямоугольные координаты Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 1). Под длиной...
-
ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ Функция называется Возрастающей на некотором Промежутке , если на этом промежутке большему значению независимой переменной...
-
Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...
-
Плоскость геометрический точка проецирование Длину отрезка АВ можно определить из прямоугольного треугольника АВС-- AС = A1B1...
-
Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий,...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
Геометрический смысл определенного интеграла - Неопределенный интеграл