Постановка задачи, Понятие о кубатурных формулах, Метод ячеек - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага
Найти при помощи метода ячеек значение интеграла

,
Где - область, ограниченная функциями
.
2. Теоретическая часть
Рассмотрим K-мерный интеграл вида:

(1)
Где - некоторая K-мерная точка. Далее для простоты все рисунки будут сделаны для случая K=2.
Понятие о кубатурных формулах
Кубатурные формулы или, иначе формулы численных кубатур предназначены для численного вычисления кратных интегралов.
Пусть функция
Определена и непрерывна в некоторой ограниченной области. В этой области выбирается система точек (узлов)

.
Для вычисления интеграла

Приближенно полагают:
(2)

Чтобы найти коэффициенты, потребуем точного выполнения кубатурной формулы (2) для всех полиномов
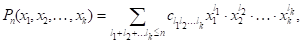
(3)
Степень которых не превышает заданного числа. Для этого необходимо и достаточно, чтобы формула (2) была точной для произведения степеней
.

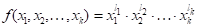
Полагая в (1) , будем иметь:

(4)
Таким образом, коэффициенты формулы (2), вообще говоря, могут быть определены из системы линейных уравнений (4).
Для того чтобы система (4) была определенной, необходимо, чтобы число неизвестных было равно числу уравнений. В случае получаем:
Метод ячеек
Рассмотрим K-мерный интеграл по пространственному параллелепипеду
.
По аналогии с формулой средних можно приближенно заменить функцию на ее значение в центральной точке параллелепипеда. Тогда интеграл легко вычисляется:
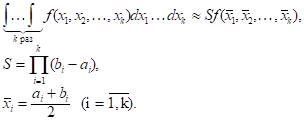
(5)
Для повышения точности можно разбить область на прямоугольные ячейки (рис. 2). Приближенно вычисляя интеграл в каждой ячейке по формуле средних и обозначая через
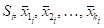
Соответственно площадь ячейки и координаты ее центра, получим:
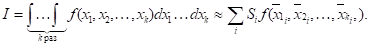
(6)
Справа стоит интегральная сумма; следовательно, для любой непрерывной
Она сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю.
Оценим погрешность интегрирования. Формула (5) по самому ее выводу точна для
.
Но непосредственной подстановкой легко убедиться, что формула точна и для любой линейной функции. В самом деле, разложим функцию по формуле Тейлора:

(7)
Где,
А все производные берутся в центре ячейки. Подставляя это разложение в правую и левую части квадратурной формулы (5) и сравнивая их, аналогично одномерному случаю легко получим выражение погрешности этой формулы:

(8)
Ибо все члены разложения, нечетные относительно центра симметрии ячейки, взаимно уничтожаются.
Пусть в обобщенной квадратурной формуле (6) стороны пространственного параллелепипеда разбиты соответственно на N1, N2, ..., Nk равных частей. Тогда погрешность интегрирования (8) для единичной ячейки равна:

Суммируя это выражение по всем ячейкам, получим погрешность обобщенной формулы:
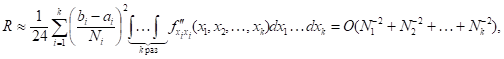
(9)
Т. е. формула имеет второй порядок точности. При этом, как и для одного измерения, можно применять метод Рунге-Ромберга, но при одном дополнительном ограничении: сетки по каждой переменной сгущаются в одинаковое число раз.
Обобщим формулу ячеек на более сложные области. Рассмотрим случай K=2. Легко сообразить, что для линейной функции
Формула типа (5) будет точна в области произвольной формы, если под S подразумевать площадь области, а под
- -координаты центра тяжести, вычисляемые по обычным формулам: (10)
Разумеется, практическую ценность это имеет только для областей простой формы, где площадь и центр тяжести легко определяется; например, для треугольника, правильного многоугольника, трапеции. Но это значит, что обобщенную формулу (6) можно применять к областям, ограниченным ломаной линией, ибо такую область всегда можно разбить на прямоугольники и треугольники.
Для области с произвольной границей формулу (6) применяют иным способом. Наложим на область сетку из K-мерных параллелепипедов (рис.3). Те ячейки сетки, все точки которых принадлежат области, назовем внутренними; если часть точек ячейки принадлежит области, а часть - нет, то назовем ячейку граничной. Объем внутренней ячейки равен произведению ее сторон. Объемом граничной ячейки будем считать объем той ее части, которая попадает внутрь ; этот объем вычислим приближенно. Эти площади подставим в (6) и вычислим интеграл.
Оценим погрешность формулы (6). В каждой внутренней ячейке ошибка составляет по отношению к значению интеграла по данной ячейке. В каждой граничной ячейке относительная ошибка есть, ибо центр ячейки не совпадает с центром тяжести входящей в интеграл части. Но самих граничных ячеек примерно в раз меньше, чем внутренних. Поэтому при суммировании по ячейкам общая погрешность будет, если функция дважды непрерывно дифференцируема; это означает второй порядок точности.
Вычисление объема граничной ячейки довольно трудоемко, ибо требует определения положения границы внутри ячейки. Можно вычислять интегралы по граничным ячейкам более грубо или вообще не включать их в сумму (6). Погрешность при этом будет, и для хорошей точности потребуется более подробная сетка.
Мы видели, что к области произвольной формы метод ячеек трудно применять; поэтому всегда желательно заменой переменных преобразовать область интегрирования в прямоугольный параллелепипед (это относится практически ко всем методам вычисления кратных интегралов).
Похожие статьи
-
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...
-
Снова рассмотрим интеграл по K-мерной области, разбитой сеткой на ячейки (рис. 2). Его можно вычислить последовательным интегрированием: Каждый...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Пусть функция непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл . (1) Геометрически число I представляет собой...
-
Приближенное вычисление определенных интегралов, Формула прямоугольников - Определенные интегралы
Задача вычисления определенного интеграла не всегда может быть сведена к первообразной, поэтому разработаны численные методы, которые позволяют найти...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Вычислить определенный интеграл по методу "Монте-Карло" по формуле , Где n - число испытаний; G(x) - плотность распределения "вспомогательной" случайной...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Решение транспортной задачи методом потенциалов - Математическая модель решения транспортной задачи
Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены. Пусть имеется транспортная задача с балансовыми условиями...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
В аналитической части изложены результаты проведенного исследования основных показателей доходов и уровня жизни населения в регионах Российской Федерации...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах Многие математические...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Модель Лефевра-Николиса описывает колебательные процессы в следующей цепочке химических реакций: Предполагается, что концентрации веществ A, B, D, E...
-
Пусть подынтегральная функция неотрицательна и ограничена: , а двумерная случайная величина распределена равномерно в прямоугольнике D с основанием и...
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Пусть в пространстве дано тело, ограниченное некоторой замкнутой поверхностью и пусть известна площадь любого его сечения, полученного плоскость,...
-
Обычно, для различных интервалов энергий используют разные типы установок, которые предназначены для измерения спектров нейтронов методом времени...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Транспортные задачи, имеющие некоторые усложнения в постановке - Экономико-математические методы
Транспортная задача с избытком запасов: Для отыскания оптимального плана вводят фиктивный (n+1)-й пункт назначения Bn+1 с потребностью bn+1 и полагают...
-
Постановка задачи - Экономико-математические методы
Пусть имеется m поставщиков А1, А2, ...,Аm однородного груза в количествах соответственно а1, а2,...,аm единиц и n потребителей В1, В2,...,Вn этого...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Заключение - Определенный интеграл
Интеграл лагранж функция коши Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Метод наименьших квадратов - Основы научных исследований
Пусть проведен однофакторный эксперимент, в котором исследована зависимость У от Х . Установлено, что основные предпосылки регрессионного анализа...
Постановка задачи, Понятие о кубатурных формулах, Метод ячеек - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага