Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач
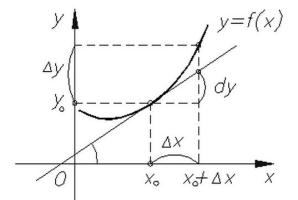
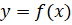
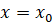
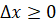
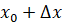
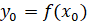
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из промежутка Х, так что и новое значениепринадлежит этому промежутку. Тогда значение функции заменится новым значением
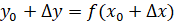
, то есть получится приращение
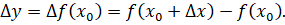
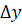
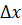
Если существует предел отношения приращения функции к вызвавшему его приращению независимой переменной при стрeмлeнии к нулю, то есть
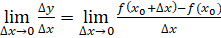
,
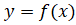
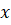
То он называется производной функции по независимой переменной при данном ее значении.
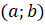
Функция, имеющая производную в каждой точке интервала называется дифференцируемой в этом интервале; опeрация нахождения производной функции называется дифференцированием. Производная функциив произвольной точке обозначается
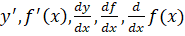
[1].
Основные правила и формулы дифференцирования
Введем правила дифференцирования арифметических действий.
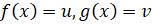
Пусть - функции, дифференцируемые в точке.
1)
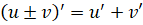
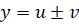
Доказательство. Обозначим. По определению производной и основным теоремам о пределах получаем:

2)
Доказательство. Обозначим. Тогда
3) , если
Доказательство. Обозначим. Тогда
Геометрический смысл производной
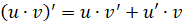
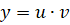
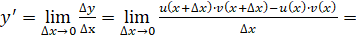
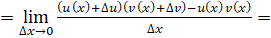
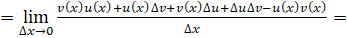
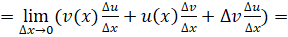
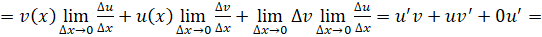
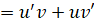
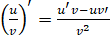
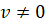
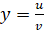
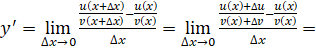
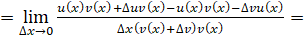
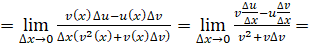
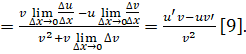
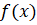
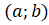
Пусть определена на некотором промежутке (рис.2). Тогда
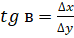
- тангенс угла наклона секущей к графику функции.
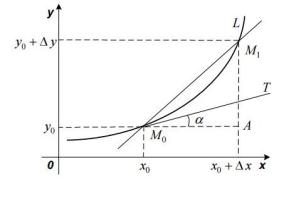
Рис.2
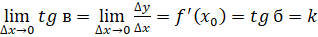
,
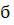
Где - угол наклона касательной к графику
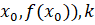
Функции в точке ( - угловой коэффициент.
Таким образом, производная в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна [1].
Уравнение касательной и нормали к графику функции, угол между ними
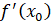
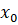
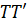
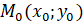
Значение производной функции в точке равно угловому коэффициенту касательной к графику этой функции, проведенной через точку, где (рис.3).
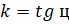
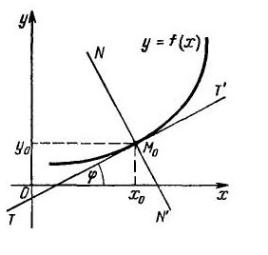
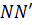
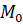
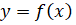
Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к графику функции в этой точке. Уравнение нормали
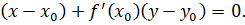
Уравнение касательной к графику функции в его точке имеет вид
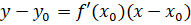
Углом между кривыми
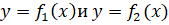
к их общей точке называется угол между касательными к этим кривым в точке. Его можно вычислить по формуле
[1].
Похожие статьи
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Стереометрические задачи - Применение производной в решении геометрических задач
Рис.7 Задача 1.Определить наибольший объем цилиндра, вписанного в конус с радиусом основания и высотой [4]. Решение. Обозначим радиус основания...
-
Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ Функция называется Возрастающей на некотором Промежутке , если на этом промежутке большему значению независимой переменной...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Заключение, Список литературы - Применение производной в решении геометрических задач
В данной работе рассмотрено решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной. В процессе выполнения...
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...
-
Тест - Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля
Модуль уравнение неравенство график В приведенном ниже тесте четыре задания на решение уравнений и неравенств, содержащих знак модуля. Используются...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Исторические сведения о производной - Применение производной в решении геометрических задач
Ряд задач дифференциального счисления был решен еще в древности. Такие задачи можно найти у Евклида и у Архимеда, но само понятие производной функции...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....
-
Частные производные высших порядков - Методы решения системы линейных уравнений
Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
События А и В называются независимыми, если Р(АВ)=Р(А)*Р(В). Пусть например бросаются две монеты; А-выпадение "герба" при первом бросании, В-выпадение...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Ответ: Функция f называется четной если для любого х из ее области определения f(-x)=f(x) График четной функции симметричен относительно оси ординат....
Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач