Розв'язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом - Лінійні різницеві рівняння зі сталими коефіцієнтами
Досить універсальним методом розв'язку лінійних однорідних систем з сталими коефіцієнтами є матричний метод. Він полягає в наступному. Розглядається лінійна система з сталими коефіцієнтами, що записана у векторно-матричному вигляді
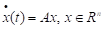
.
Робиться невироджене перетворення:
,
Де вектор - нова невідома векторна функція.
Тоді рівняння прийме вигляд
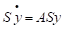
або.
Для довільної матриці завжди існує неособлива матриця, що приводить її до жорданової форми, тобто
,
Де - жорданова форма матриці. І система диференціальних рівнянь прийме вигляд
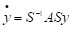
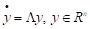
.
Складемо характеристичне рівняння матриці
, або.
Алгебраїчне рівняння - го ступеня має коренів. Розглянемо різні випадки.
1. Нехай - дійсні різні числа. Тоді матриця має вигляд

.
І перетворена система диференціальних рівнянь розпадається на - незалежних рівнянь
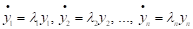
.
Розв'язуючи кожне окремо, отримаємо
.
Або в матричному вигляді
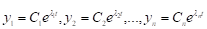
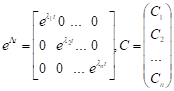
Де.
Звідси розв'язок вихідного рівняння має вигляд
.
Для знаходження матриці треба розв'язати матричне рівняння
або,
Де - жорданова форма матриці.
Якщо матрицю записати у вигляді
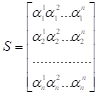
,
То для кожного з стовпчиків, матричне рівняння перетвориться до
, .
Таким чином, у випадку різних дійсних власних чисел матриця являє собою набір - власних векторів, що відповідають різним власним числам.
- 2. Нехай - комплексний корінь. Тоді відповідна клітка Жордана має вигляд
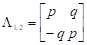
,
А перетворена система диференціальних рівнянь
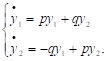
Неважко перевірити, що розв'язок отриманої системи диференціальних рівнянь має вигляд
Або в матричному вигляді
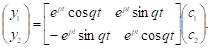
Таким чином, комплексно-спряженим власним числам
Відповідає розв'язок
Де
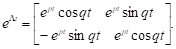
3. Нехай - кратний корінь, кратності, тобто і йому відповідають лінійно незалежних векторів. Тоді клітка Жордана, що відповідає цьому власному числу, має вид
І перетворена підсистема, що відповідає власному числу, розпадається не дві підсистеми
.
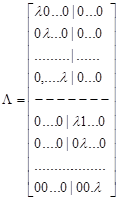
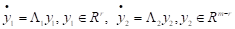
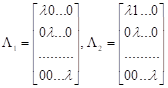
.
Розв'язок першої знаходиться з використанням зазначеного в першому пункті підходу. Розглянемо другу підсистему. Запишемо її в координатному вигляді
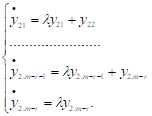
Розв'язок останнього рівняння цієї підсистеми має вигляд
.
Підставимо його в передостаннє рівняння. Одержуємо:
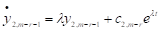
.
Загальний розв'язок лінійного неоднорідного рівняння має вигляд суми загального розв'язку однорідного і частинного розв'язку неоднорідних рівнянь, тобто
.
Загальний розв'язок однорідного має вигляд
.
Частинний розв'язок неоднорідного шукаємо методом невизначених коефіцієнтів у вигляді
,
Де - невідома стала.
Підставивши в неоднорідне рівняння, одержимо
.
Звідси
І загальний розв'язок неоднорідного рівняння має вигляд
.
Піднявшись ще на один крок нагору одержимо
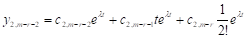
.
Продовжуючи процес далі, маємо
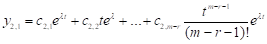
.
Або у векторно-матричному вигляді
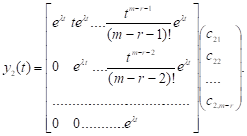
.
Додавши першу підсистему, одержимо
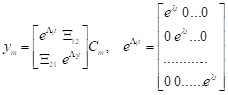
,
Для останніх двох випадків матриця знаходиться як розв'язок матричного рівняння
.
Похожие статьи
-
Система диференціальних рівнянь, що записана у вигляді Чи у векторно-матричному вигляді Називається системою лінійних неоднорідних диференціальних...
-
Система диференціальних рівнянь вигляду Де - сталі величини, називається лінійною однорідною системою з сталими коефіцієнтами. У матричному вигляді вона...
-
Задача Коші - Лінійні різницеві рівняння зі сталими коефіцієнтами
Нехай - фундаментальна система, нормована при тобто , Де - одинична матриця. Загальний розв'язок однорідної системи має вигляд . Вважаючи невідомою...
-
Визначення. Матриця називається оберненою матриці, якщо їх добуток, тобто рівний одиничній матриці. Якщо квадратна матриця має зворотню матрицю, то вона...
-
Розв'язання систем рівнянь, Порядок виконання роботи - Вивчення математичного пакету MathСad
Матриця математичний пакет арифметичний Для розв'язання системи рівнянь з кількома невідомими треба задати початкові наближення для кожної змінної. Далі...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
Метод Гауса - Основи вищої математики
( Карл Фрідріх Гаус (1777-1855) іноземний член Петербурзької АН (1824), німецький математик. Праці: вища алгебра, диференціальна геометрія, математична...
-
Системи лінійних алгебраїчних рівнянь - Основи вищої математики
1. Будемо розглядати систему з "m" лінійних алгебраїчних рівнянь із "n" невідомими (8.1) Рішенням такої системи називається такий набір чисел Х 1, Х 2,...
-
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно...
-
Характеристичний багаточлен матриці, Розв'язання рівнянь - Вивчення математичного пакету MathСad
Для побудови характеристичного багаточлена матриці A використаємо символьні обчислення. Побудуємо матрицю D = A - Е, віднявши з діагональних елементів...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Метод Монте-Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для...
-
Біологія . Необхідно знайти залежність площі молодого листка, що має форму круга, від часу. Відомо, що швидкість зміни площі в момент пропорцією площі...
-
Заключение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Метод обобщенных интервальных оценок, предложенный в настоящей статье, является новым методом представления экспертных знаний в задачах, исходные данные...
-
В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
Заключение - Моделирование систем массового обслуживания с использованием метода Монте-Карло
Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Возникновение идеи...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Введение - Изучение методов жидких и газообразных и однородных неоднородных систем
Гомогенная система -- однородная система, химический состав и физические свойства которой во всех частях одинаковы или меняются непрерывно (между частями...
-
Модель "вход - выход" для нестационарной системы управления можно представить в следующем виде [2] . Где коэффициенты матриц возмущения и ограничены...
-
Реализация интеллектуальных систем поддержки решений (ИСППР) в задачах оценки перспективности объектов природопользования на ранних стадиях их...
-
Вступ, Необхідні відомості з теорії матриць - Невід'ємні матриці
Відомо [[1]-[10]], яку важливу роль відіграють невід'ємні матриці в математичних моделях економіки, біології, теорії ймовірностей тощо. Одними з...
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
ЗАТ "Біола" випускає три види продукції: напій на основі сиропу з цукром, напій на основі сиропу з цукрозамінником, сік. У поточному місяці прогнозуються...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
Зв'язок між визначеним та невизначеним інтегралами Означення 2. Визначений інтеграл з постійною нижньою межею та змінною верхньою межею називають...
-
Дана група методів є однією з найбільш поширених в системі прогнозування економічних явищ, зокрема і перспективного попиту на продукцію вугільної...
-
ОПРЕДЕЛЕНИЕ МЕТОДА ФАКТОРНОГО АНАЛИЗА И ЧИСЛА ФАКТОРОВ - Многомерный статистический анализ
Определение метода факторного анализа. Различные методы факторного анализа различаются в зависимости от подходов, которые используются для выделения...
-
Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе G...
-
Попит і пропозиція - економічній категорії товарного виробництва. Попит - представлена на ринку потреба в товарах, Пропозиція - продукт, який є на ринку...
-
Межотраслевой баланс в прогнозировании Развития экономики Экономика стран на современном этапе представляет собой сложный многоотраслевой комплекс с...
-
Основные направления совершенствования организационной структуры предприятия ОАО "Огонек". Любую перестройку структуры управления необходимо оценивать, в...
-
Равноускоренное (равнозамедленное) развитие. Этому типу динамики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов...
-
Статистические испытания схемы проводятся исходя из того, что генерирование случайных логических переменных xI проводится с помощью равномерного...
-
Диспергированием называют тонкое измельчение твердых мате-риалов или жидкостей и распределение их частиц в жидкой или газообразной среде, в результате...
-
Конденсационные методы получения коллоидных систем - Методы очистки и получения коллоидных растворов
Из классификации дисперсных систем по размеру частиц следует, что коллоидные растворы (золи) занимают промежуточное положе-ние между молекулярными и...
-
Особенности эконометрического метода Эконометрическая модель -- основное понятие эконометрии, экономико-математическая модель, параметры которой...
Розв'язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом - Лінійні різницеві рівняння зі сталими коефіцієнтами