Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений
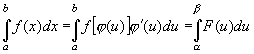
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa и Cosb = Sina (т. е. Cosa и Cosb - косинусы углов, образованных лучом l с положительным направлением осей координат Ох и Оу).
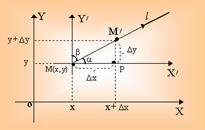
Рис. 14.1. |
При перемещении в данном направлении l точки М(х, у) в точку М/(х + Dх, у + Dу) О w функция u = f(x, y) получает приращение
Du = f(х + Dх, у + Dу) - f(x, y), (14.1)
Которое называется приращением функции u в данном направлении.
Если ММ/ = Dl есть величина перемещения точки М, то из DМРМ/ получаем
(14.2)
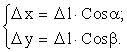
Следовательно, DL u = f(х + Dх, у + Dу) - f(x, y).
Определение 14.1. Под производной функции u в данном направлении к величине перемещения при условии, что последняя стремится к нулю, т. е.
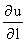
. (14.3)
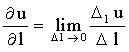
Тогда частные производные, можно рассматривать как производные функции u в положительных направлениях осей координат Ох и Оу. Производная дает скорость изменения функции в направлении l.
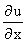
Пусть u = f(x, y) - дифференцируема. Тогда, используя формулу полного дифференциала, будем иметь
,
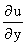
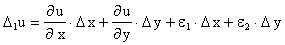
Где e1 ® 0, e2 ® 0 при Dх ® 0, Dу ® 0. Тогда в силу соотношений (14.2) получаем
И, переходя к пределу при Dl ® 0 , что то же самое, что и Dх ® 0, Dу ® 0, имеем
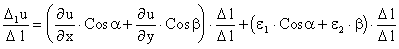
. (14.4)
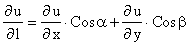
Замечание. Пусть u=f(x, y,z). Ее производная в направлении
L = нСos a, Cos b, Cos gэ будет.
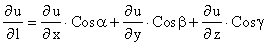
Градиент и его свойства
Определение 14.2. Говорят, что в данной области w определено скалярное поле, если для каждой точки М О w задан некоторый скаляр (т. е. число)
U = f(M). (14.5)
Следовательно, U есть числовая функция точки.
Примерами скалярных полей являются:
- - температурное поле (т. е. распределение температуры в нагретом теле); - концентрация вещества в растворе.
Рис. 14.2. |
Пусть w (т. е. область) расположена на плоскости Оху; тогда любая ее точка определена координатами (х, у). При этом плоское скалярное поле (14.5) может быть записано в виде
U = f(х, у), ((х, у) О w).
Аналогично в пространстве ОХуz
U = f(х, у,z), ((х, у,z) О w)
Таким образом, понятие скалярного поля представляет собой физическую трактовку функции нескольких переменных.
Определение 14.3. Будем говорить, что в данной области w определено векторное поле, если для каждой точки М О w задан некоторый вектор
(14.6)
Примеры.
- 1. Поле скоростей в данный момент времени точек потока жидкости. 2. Силовое поле, создаваемое некоторым притягивающим центром.
Для плоского векторного поля (14.6) мы будем иметь вектор-функцию
A = F(x, y), ((х, у) О w) (14.7)
Отсюда, переходя к координатам вектора а, получим
АX = F1(x, y), аY = F2(x, y).
Таким образом, задание плоского векторного поля (14.7) равносильно заданию двух скалярных полей.
Аналогично для случая пространственного векторного поля
A = F(х, у,z), ((х, у,z) О w);
АX = F1(x, y,z),
АY = F2(x, y,z), (14.8)
АZ = F1(x, y,z).
В этом случае векторное поле эквивалентно трем скалярным полям.
Множество точек М, для которых скалярное поле (14.5) сохраняет постоянное значение f(M) = const, называется поверхностью (или линией) уровня скалярного поля (изоповерхностью).
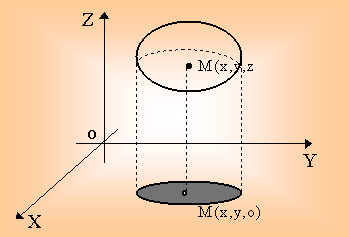
Рис. 14.3. |
|
Рис. 14.4. |
Т. е. изоповерхность - это множество всех точек пространства ОXyz, где данная функция имеет одно и то же значение.
Определение 14.4. Пусть U=f(х, у) - дифференцируемая плоское скалярное поле (функция двух переменных). Тогда вектор
(14.9)
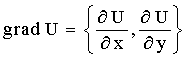
Называется градиентом поля.
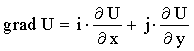
Аналогично для пространства
Пусть U=f(х, у) - пространственное скалярное поле, тогда его градиент есть вектор
.
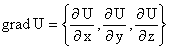
Таким образом, скалярное поле порождает векторное поле - поле градиентов.
Под производной скалярного поля в данном направлении l понимаем
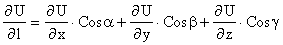
Производная представляет собой скорость изменения поля в данном направлении.
Похожие статьи
-
Частные производные высших порядков - Методы решения системы линейных уравнений
Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...
-
Элементарные преобразования, Миноры - Методы решения системы линейных уравнений
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...
-
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах Многие математические...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Односторонние пределы, Пределы на бесконечности - Свойства функций
В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений