Примеры решения - Элементы теории вероятностей и математической статистики
Задача 1. Из 25 контрольных работ, среди которых 5 оценены на "отлично", наугад извлекают 3 работы. Составить закон распределения случайной величины Х - числа работ, оцененных на "отлично", среди отобранных работ. Найти функцию распределения F(X) случайной величины X и построить ее график. Найти для X ее среднее значение (математическое ожидание M(X)), дисперсию D(X), среднее квадратическое отклонение и моду. Найти вероятность, где A=x2, b=xN-1 двумя способами: используя функцию распределения и непосредственно по таблице распределения.
Решение: Пусть случайная величина X - число работ, оцененных на "отлично" среди трех отобранных. Так как из 25 контрольных работ 5 оценены на "отлично" и выбирается из них 3 работы, то случайная величина X может принимать следующие значения:
Найдем вероятности того, что случайная величина Х Примет соответствующие значения. Заметим, что решение задачи о нахождении вероятности события (Х=0), то есть Р(Х=0), Как впрочем, и решение задач о нахождении следующих вероятностей Р(Х=1), Р(Х=2), Р(Х=3), Может быть найдено с помощью известной формулы:

Где N- общее количество исходов, M - количество исходов, благоприятствующих появлению события А.
В этой задаче событие А Состоит в том, что среди отобранных работ, число работ, оцененных на "отлично", равно K; K последовательно принимает значения 0, 1, 2 и 3; N - количество способов выбора трех работ из 25 - общего количества работ; M - количество способов выбора K работ, оцененных на "отлично", из общего количества работ.
Предварительно найдем число сочетаний из 25 по 3 (число способов, которыми можно из 25 контрольных работ извлечь 3):

.
Для (X=0) число исходов, благоприятствующих появлению события А, Может быть вычислено по формуле:

.
Тогда.
.
.




.
Тогда искомый закон распределения примет вид:
|
X |
0 |
1 |
2 |
3 |
|
Pi |
0,496 |
0,413 |
0,087 |
0,004 |
Убедимся, что сумма вероятностей равна единице:

.
Проведем все эти расчеты в MS Excel.
Математическое ожидание (среднее значение) дискретной случайной величины X найдем по формуле (1.3). Пример реализации в MS Excel дан на рис. 1.3, интервал D20:D25. дискретная непрерывная случайная вероятность
В результате получаем .
Дисперсию дискретной случайной величины X найдем двумя способами.
Первый способ - по формуле (1.5), по определению дисперсии. Эти вычисления реализованы в MS Excel (рис. 1.3), интервал ячеек F20:F25.
В результате получаем .
Второй способ - по формуле (1.6) по свойству дисперсии. Предварительно необходимо вычислить математическое ожидание квадрата дискретной случайной величины X - . Пример реализации в MS Excel дан на рис. 1.3, интервал ячеек E20:E25. В результате получаем .
Тогда дисперсия равна:
.
Оба значения, полученные разными способами, совпали.
Среднее квадратическое отклонение:
.
Вычислим моду. Для этого можно по таблице распределения (интервал B20:C25) найти XI, которому соответствует наибольшее значение вероятности PI.
Другой способ - анализируя полигон распределения, найдем XI, которому соответствует самое большое значение PI. Очевидно, что =0.
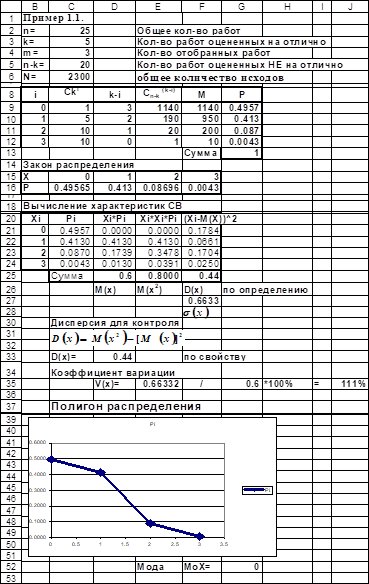
Рис. 1.3. Решение задачи 1 в MS Excel (начало)
Вычислим коэффициент вариации V(Х) по формуле (1.8):

.
Построим многоугольник распределения по заданному распределению, используя графические средства MS Excel.
Для нахождения функции распределения воспользуемся формулой (1.11).
В нашем примере имеем:

Таким образом, функция распределения примет вид:

.
Рис. 1.4. Решение задачи 1 в MS Excel (окончание)
В MS Excel эти расчеты реализованы в интервале ячеек D55:D59 (рис. 1.4), на том же листе построена "заготовка" для графика функции распределения. Далее эту "заготовку" следует достроить вручную до корректного графика (нанести стрелки и подписи по оси ординат), как на рис. 1.2. Эту операцию по превращению полученной диаграммы EXCEL в корректную функцию распределения необходимо производить для всех распределений в данной работе (рис. 1.6 и рис. 1.8).
Найдем вероятность, где A=x2, B=xN.
В данном случае X2=1, XN=3, т. е. требуется найти.
Первый способ - используем функцию распределения:
.
Второй способ - по таблице распределения.
Событие, состоящее в том, что СВ Х примет значения в промежутке может реализоваться только в том случае, когда СВ принимает значения или. Таким образом,
.
Задача 2. Стрелок производит три выстрела в цель. Вероятность попадания в цель при каждом выстреле равна 0,2. Составить закон распределения числа попаданий в цель (случайная величина X). Найти функцию распределения случайной величины X F(X) и построить ее график. Найти среднее значение (математическое ожидание) M(X), дисперсию D(X) и моду СВ Х. Найти вероятность, где A=x2, B=xN-1 двумя способами: с помощью функции распределения и непосредственно по таблице распределения СВ Х.
Решение: Пусть случайная величина X - число попаданий в цель при трех выстрелах.
Обозначим N - число выстрелов, Р- вероятность попадания при каждом выстреле, Q - Вероятность промаха при каждом выстреле Q =1- р. По условию имеем Р=0,2; Q=0,8; n=3.
Заметим, что при N=3 Случайная величина X может принимать следующие значения: Х 1=0, х 2=1, х 3=2, х 4=3. Отметим, что испытания проводятся по схеме Бернулли. Действительно, число испытаний конечно и каждое испытание является независимым. В каждом испытании наблюдается либо "успех" (попал в цель), либо "неуспех" (не попал в цель или промахнулся). Вероятность удачи в каждом испытании постоянна. Так как испытания проводятся по схеме Бернулли, то можно утверждать, что случайная величина X имеет биномиальное распределение и соответствующие вероятности вычисляются по формуле Бернулли:
Найдем соответствующие вероятности для данного примера:
.
.
.
.
Тогда искомый закон распределения примет вид:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,512 |
0,384 |
0,096 |
0,008 |
Убедимся, что сумма вероятностей равна единице:

.
Заметим, что для биномиального распределения математическое ожидание и дисперсию легко вычислить по формулам:
Математическое ожидание M(X)= n p =3- 0,2 =0,6;
Дисперсия D(X) = n p q =3- 0,2 -0,8 = 0,48.
Найдем вероятность, где A=x2, b=xN. В данном случае X2=1, XN=3, т. е. требуется найти.
Первый способ - используя функцию распределения.
.
Второй способ - по таблице распределения.
Событие, состоящее в том, что СВ примет значения в промежутке может реализоваться только в том случае, когда СВ равна 1 или 2. Таким образом,
.
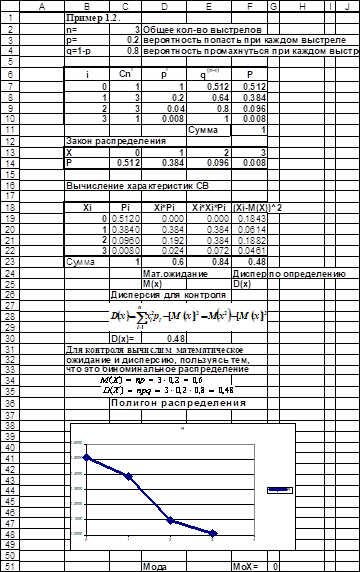
Рис. 1.5. Решение задачи 2 в MS Excel
Рис. 1.6. Решение задачи 2 в MS Excel (продолжение)
Задача 3. Телефонная станция получает в час в среднем 300 вызовов.
Составить закон распределения количества вызовов, полученных станцией за одну минуту (случайная величина X). Построить Многоугольник (Полигон) распределения для иллюстрации распределения СВ X. Найти среднее значение (математическое ожидание M(X)), дисперсию D(X), среднее квадратическое отклонение и моду СВ X. Вычисление математического ожидания M(X)), дисперсии D(X), среднее квадратического отклонения провести двумя способами: приближенно, используя таблицу распределения, взяв первые 20 значений СВ, и аналитически, используя тот факт, что рассматривается распределение Пуассона.
Найти функцию распределения F(X) случайной величины X и построить ее график. Какова вероятность того, что за одну минуту станция получит не менее 4 вызовов и не более 8?
Решение: Проведем все вычисления в MS Excel, рис. 1.7-1.8.
Очевидно, что СВ X - количество вызовов, полученных станцией за одну минуту, распределено по закону Пуассона. Определим параметр л. В данном случае л=N/60 =300/60=5.
Распределение Пуассона определяется соотношением (1.14), для данной задачи:

На рис. 1.7 в интервале ячеек A5:B26 представлены первые 20 значений искомого распределения. Ячейка B6 содержит формулу:
B6=$C$4^A6/ФАКТР(A6)*EXP(-$C$4),
Остальные значения этого столбца заполняются копированием.
Вычисление Математического ожидания M(X)), дисперсии D(X), среднего квадратического отклонения выполнено по формулам (1.3)-(1.6). Порядок вычисления такой же, как в задачах 1 и 2. Заметим, что эти формулы в данном случае не являются точными, поскольку случайная величина принимает бесконечное множество значений, а в вычислениях удержаны только 20 первых слагаемых (погрешность можно вычислить самостоятельно). Тогда, M(X)=л=4,999998; D(X)=л=4,999978;

.
Аналитически вычисление математического ожидания M(X), дисперсии D(X), среднего квадратического отклонения исключительно просто.
M(X)=л=5, D(X)=л=5, .
Сравнивая вычисленные характеристики, приходим к выводу, что результаты совпадают с точностью до 10-5.
Коэффициент вариации V(x):

.
Данное распределение двумодальное (имеет два одинаковых наибольших значения). Очевидно, что равна 4 и 5.
Многоугольник (или Полигон) распределения Построен на рабочем листе в строках 35:50.
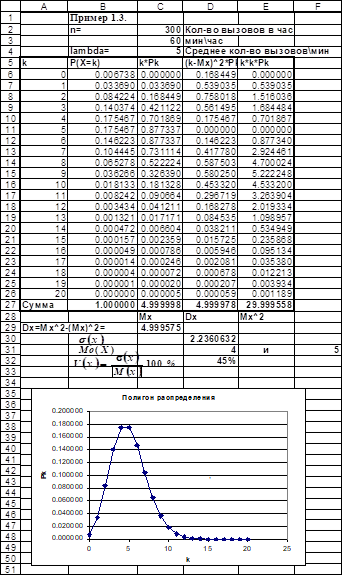
Рис. 1.7. Решение задачи 3 в MS Excel (начало)
Найдем приближенно функцию распределения F(X) случайной величины X и построим ее график. Таблица значений функции распределения для первых 12 интервалов приведена в строках 52:67, график функции распределения для первых 12 интервалов приведен в строках 67:89.
Найдем вероятность того, что за одну минуту станция получит не менее 4 и не более 8 вызовов, т. е. найдем.
Первый способ использует функцию распределения:
,
Тогда,
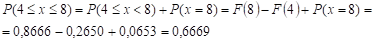
Рис. 1.8. Решение задачи 3 в MS Excel (окончание)
Второй способ использует непосредственно таблицу распределения.
Очевидна следующая формула:

Для вычисления по этой формуле в ячейку H96 введем формулу:
H96 =СУММ(B10:B14),
В результате получим то же значение, равное 0,6669 (рис. 1.9).
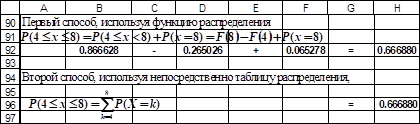
Рис. 1.9. Решение задачи 3 в MS Excel
Похожие статьи
-
Цель: освоить на практике нахождение с помощью MS EXCEL числовых характеристик дискретных случайных величин, а также изучить основные свойства функции...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
Распределение Пуассона - Элементы теории вероятностей и математической статистики
Распределение Пуассона является дискретным распределением и описывается формулой: , (1.14) Где л>0-параметр распределения. Этот закон используют для...
-
Контрольная работа По дисциплине: Теория вероятностей Контрольная работа № 1 Вариант 1 Задача № 1 Условие: Из 10 изделий, среди которых 4 бракованные,...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
Непрерывные величины - возможные значение, которых непрерывно заполняют некоторый диапазон. Плотность распределения вероятности непрерывной случайной...
-
ЗАКЛЮЧЕНИЕ - Основные методы математического моделирования для принятия управленческих решений
В данной работе поставленная цель была достигнута. Мы рассмотрели основные методы математического моделирования (принятия решений) на практике, а именно:...
-
Биноминальное распределение - Элементы теории вероятностей и математической статистики
Допустим, что выполняется серия из N независимых одинаковых испытаний. Испытания независимы в том смысле, что результаты одних испытаний не влияют на...
-
1. Если значения измеренного признака не отличаются друг от друга (равны между собой) - дисперсия равна нулю. Это соответствует отсутствию изменчивости в...
-
Системы массового обслуживания -- это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки...
-
Классический способ задания вероятности. Примеры, Элементы комбинаторики - Теория вероятности
При данном способе пространство элементарных событий является конечным, и все элементарные события равновероятны. Тогда вероятность события определяется...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
применяем 2е теоремы: -формула полной вероятности Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H1, H2, ..., Hn...
-
Обозначим вероятность соответствующих событий через Pi - Случайные величины
, Так как рассматриваемые события образуют полную группу не совместных событий, то Х полностью описана с вероятностной точки зрения, если мы зададим...
-
Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин
Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится. Не будет лишним помнить, что этот...
-
Распределением признака Называется закономерность встречаемости разных его значений. Нормальное распределение Характеризуется тем, что крайние значения...
-
Статистическая неопределенность и процедуры со многими решениями Все существующие методы фильтрации (минимальное остовное дерево, максимальный плоский...
-
Пусть у игроков А и В соответственно M и N чистых стратегий, которые обозначим через и. Выбор игроками любой пары стратегий и однозначно определяет исход...
-
Математическое ожидание генеральной совокупности назовем генеральной средней, т. е. . Теорема. Выборочное среднее есть состоятельная и несмещенная оценка...
-
Необходимо провести прогноз товарооборота магазина "Ткани для дома" на тринадцатый день. Исходные данные: Таблица 2.1 - Ежедневный товарооборот магазина...
-
Математическое ожидание - Основы научных исследований
Интегральная и дифференциальная функции распределения являются исчерпывающими статистическими характеристиками любой случайной величины. Однако многие...
-
Вопросы по теории вероятностей - Случайные величины
Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. Сумма и произведение событий, теоремы сложения и...
-
Признаки Х и Y находятся в Корреляционной зависимости , если каждому значению одного признака X I соответствует определенная Условная средняя другого...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
В экономической сфере деятельности в современных условиях большое значение имеет принятие решений. Для принятия экономических решений в нынешних условиях...
-
ПРИМЕРЫ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ, ПРИМЕР 1 - Виды математических моделей
В этом разделе рассмотрим типичные примеры составления математических моделей для решения самых различных задач, как народного хозяйства, так и школьных...
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Методы непараметрической статистики - Основы теории систем и системного анализа
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что...
-
События А и В называются независимыми, если Р(АВ)=Р(А)*Р(В). Пусть например бросаются две монеты; А-выпадение "герба" при первом бросании, В-выпадение...
-
Вероятность - математическая оценка возможности появления это события в результате опыта - обозначается Р (А).- при условии :0 ?Р (А)?1, Р (?...
-
Рассмотрим конечные матричные игры, в которых нет седловой точки, т. е. . Нетрудно доказать, что. Если игра одноходовая, то по принципу минимакса игроку...
-
Вероятностные характеристики полумарковской модели Формулы для условных вероятностей Обозначим Теорема 1. В рассматриваемой стохастической полумарковской...
-
Статистики, Свойства оценок - Основы научных исследований
Любая функция от элементов выборки называется Статистикой . Следовательно, точечная оценка также является статистикой. Однако не всякая статистика может...
-
Законы распределений дискретных случайных величин. - Распределение вероятности случайных величин
Пусть некоторая СВ является дискретной, т. е. может принимать лишь фиксированные (на некоторой шкале) значения X I. В этом случае ряд значений...
-
Значит и Вторая теорема двойственности (теорема о дополняющей нежесткости) Пусть - допустимое решение прямой задачи, а - допустимое решение двойственной...
-
Теоретическое описание методов решения задания, СМО с отказами - Теория массового обслуживания
СМО с отказами Одноканальная система (СМО) с отказами Имеется один канал, на который поступает поток заявок с интенсивностью л, поток обслуживания имеет...
Примеры решения - Элементы теории вероятностей и математической статистики