Точечная оценка математического ожидания, Свойства математического ожидания, Заключение - Математическое ожидание случайной величины
Математическое ожидание генеральной совокупности назовем генеральной средней, т. е.
.
Теорема. Выборочное среднее есть состоятельная и несмещенная оценка генеральной средней.
Доказательство. Вначале покажем, что есть состоятельная оценка для, т. е.
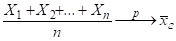
.
По следствию из теоремы Чебышева для одинаково распределенных случайных величин имеем
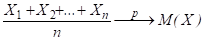
.
Так как, то используя свойства математического ожидания, получим
Свойства математического ожидания
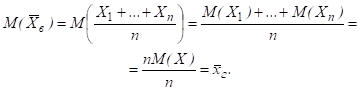
Для случайной величины дискретного типа (СВДТ) и непрерывного типа (СВНТ) математическое ожидание находится по формулам [4]
MX = M[X] =
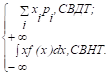
Математическое ожидание существует, если ряд (соответственно интеграл) в правой части формулы сходится абсолютно. Если mX = 0, то СВ Х называется центрированной (обозначается ).
Свойства математического ожидания:
M[C] = C, где С - константа;
M[CX] = CM[X];
M[X+Y] = M[X]+M[Y], для любых СВ X и Y;
Заключение
Математическое ожидание - одно из центральных понятий математической статистики, отражает наиболее ожидаемое значение случайной величины. Но она является хорошей характеристикой, когда плотность распределения "симметрична", как у нормального закона [2]. В ином случае она не является адекватной характеристикой. Тем не менее, математическое ожидание используется для определения законов распределения, проверки множества гипотез и имеет огромное значение в статистике и многих других дисциплин, используется в практической деятельности.
Похожие статьи
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
Генеральная и выборочная совокупности Для обнаружения закономерностей, описывающих исследуемое массовое явление, необходимо иметь опытные данные,...
-
Введение - Математическое ожидание случайной величины
Математическая статистика - наука, изучающая методы исследования закономерностей в массовых случайных явлениях и процессах по данным, полученным из...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
применяем 2е теоремы: -формула полной вероятности Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H1, H2, ..., Hn...
-
Статистики, Свойства оценок - Основы научных исследований
Любая функция от элементов выборки называется Статистикой . Следовательно, точечная оценка также является статистикой. Однако не всякая статистика может...
-
Математическое ожидание - Основы научных исследований
Интегральная и дифференциальная функции распределения являются исчерпывающими статистическими характеристиками любой случайной величины. Однако многие...
-
Вариационные ряды - Математическое ожидание случайной величины
После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине - т. е....
-
Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин
Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится. Не будет лишним помнить, что этот...
-
Обозначим вероятность соответствующих событий через Pi - Случайные величины
, Так как рассматриваемые события образуют полную группу не совместных событий, то Х полностью описана с вероятностной точки зрения, если мы зададим...
-
Нормальное распределение - Распределение вероятности случайных величин
Первым, фундаментальным по значимости, является т. н. Нормальный закон Распределения непрерывной случайной величины X, для которой допустимым является...
-
Свойства выборочной совокупности - Математическое ожидание случайной величины
Для того чтобы по отобранным значениям некоторого количественного показателя можно было достаточно уверенно судить обо всей совокупности, полученная...
-
Литература - Математическое ожидание случайной величины
1. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977. 2. Гмурман В. Е. Руководство к решению задач по теории...
-
Распределения непрерывных случайных величин - Распределение вероятности случайных величин
До этого момента мы ограничивались только одной "разновидностью" СВ - дискретными, т. е. принимающими конечные, заранее оговоренные значения на любой из...
-
Законы распределений дискретных случайных величин. - Распределение вероятности случайных величин
Пусть некоторая СВ является дискретной, т. е. может принимать лишь фиксированные (на некоторой шкале) значения X I. В этом случае ряд значений...
-
В общем случае: , где Для не корреляционных случайных величин: Ответ на билет 15 В широком смысле слова, закон больших чисел характеризует устойчивость...
-
Вопросы по теории вероятностей - Случайные величины
Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. Сумма и произведение событий, теоремы сложения и...
-
Односторонние и двухсторонние значения вероятностей - Распределение вероятности случайных величин
Если нам известен закон распределения СВ (пусть - дискретной), то в этом случае очень часто приходится решать задачи, по крайней мере, трех стандартных...
-
Большую роль в теории и практике системного анализа играют некоторые стандартные распределения непрерывных и дискретных СВ. Эти распределения иногда...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Непрерывные величины - возможные значение, которых непрерывно заполняют некоторый диапазон. Плотность распределения вероятности непрерывной случайной...
-
Шкалирование случайных величин - Распределение вероятности случайных величин
Как уже отмечалось, дискретной называют величину, которая может принимать одно из счетного множества так называемых "допустимых" значений. Примеров...
-
Распределением признака Называется закономерность встречаемости разных его значений. Нормальное распределение Характеризуется тем, что крайние значения...
-
1. Если значения измеренного признака не отличаются друг от друга (равны между собой) - дисперсия равна нулю. Это соответствует отсутствию изменчивости в...
-
Пусть есть математическое ожидание цены состояния объекта при условии, что в момент времени tдопустимое экологическое состояние не достигнуто и цена...
-
Статистическая вероятность и распределения случайных величин - Основы научных исследований
В теории вероятностей под случайной величиной понимают отношения числа благоприятных исходов испытаний к общему числу испытаний. Например, если из 10...
-
Методы классификации - неотъемлемая часть математических методов исследования, интересная теоретически и важная практически. Обзоры этой научной области...
-
Ответ: В педагогических исследованиях прикладная направленность математики, понимается как содержательная и методическая связь курса математики с...
-
Пусть у нас имеется некоторая непрерывная случайная величина X, распределенная нормально с математическим ожиданием и среднеквадратичным отклонением....
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Общая схема метода Монте-Карло Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Данная контрольная работа состоит из двух частей - теоретической и практической. В теоретической части будет подробно рассмотрена такая важная...
-
Случайные события и случайные величины - Основы научных исследований
Вероятностные закономерности проявляются только в массовых явлениях, т. е. когда один и тот же объект изменяет свое состояние многократно или когда...
-
Взаимосвязи случайных событий - Закон распределения случайной величины
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти)....
-
Заключение, Список литературы - Степенные величины в статистике
Средние величины имеют большое распространение в статистике коммерческой деятельности. В средних величинах отображаются важнейшие показатели...
-
Выборочные распределения на шкалах Int и Rel
Оценка наблюдений при неизвестном законе распределения Какова цель наблюдений над случайной величиной; для чего используются результаты наблюдений; где,...
Точечная оценка математического ожидания, Свойства математического ожидания, Заключение - Математическое ожидание случайной величины