Лабораторная работа 1. Вычисление числовых характеристик дискретной случайной величины, Базовые понятия - Элементы теории вероятностей и математической статистики

Цель: освоить на практике нахождение с помощью MS EXCEL числовых характеристик дискретных случайных величин, а также изучить основные свойства функции распределения.

Базовые понятия

Различают дискретные и непрерывные случайные величины (СВ).

Дискретной Случайной величиной Называют такую СВ, которая принимает отдельные, изолированные значения с определенными вероятностями. Например, число покупателей в магазине в определенный момент времени, количество определенного товара, продаваемого ежедневно в магазине, число автомобилей на проспекте и т. д. являются дискретными СВ. Дискретность распределения не означает его конечность. Существуют дискретные распределения, которые имеют бесконечное количество возможных исходов. Одним из них является распределение Пуассона.

Для описания дискретной СВ необходимо установить соответствие между всевозможными значениями СВ и их вероятностями. Такое соответствие называется Законом распределения дискретной СВ. Его можно задать таблично, аналитически (в виде формулы), либо графически.

Например, табличное задание закона распределения дискретной СВ (табл.1.1):

Таблица 1.1

Х

Х 1

Х 2

...

Хn

Рi

Р 1

Р 2

...

Рn

Где ХI - Значение случайной величины;

Р 1- Вероятность, с которой СВ принимает значение ХI.

При этом должны выполняться следующие соотношения:

и (1.1)

Эта таблица показывает что, случайная величина X в результате испытания может принять одно из возможных значений Х 1, х 2,..., хП с соответствующими вероятностями

Р (Х = х 1) = р 1; Р(Х = х 2) = р 2; ... Р(Х = хП) = рN. (1.2)

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной декартовой системе координат строят точки с координатами и соединяют их последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения (полигоном) случайной величины X.

Случайные величины описываются некоторыми числовыми Характеристиками. Важнейшими из них являются: математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Математическое ожидание М(Х) для дискретной СВ определяется по формуле:

, (1.3)

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений СВ при многократной реализации случайной величины.

Дисперсией D(X) CВ X называется математическое ожидание квадрата отклонения СВ от ее математического ожидания:

(1.4)

При этом для дискретной СВ имеем:

(1.5)

На практике, для вычисления дисперсии используется формула:

(1.6)

Следует помнить, что формула (1.4) - это определение дисперсии, а соотношение (1.6) - это Свойство, которое доказывается в теории вероятностей.

Из определения дисперсии следует, что это Мера рассеяния (разброса) Всех возможных значений случайной величины относительно среднего ожидаемого значения. Дисперсия характеризует изменчивость случайной величины: чем она больше, тем дальше от среднего значения находятся возможные значения случайной величины.

Так как дисперсия имеет размерность, равную квадрату размерности СВ, а это неудобно, то вводится другая числовая характеристика - среднее квадратическое отклонение.

Средним квадратическим отклонением или Стандартным отклонением- СВ Х называют величину:

(1.7)

Для оценки разброса значений СВ в процентах относительно ее среднего значения, вводится Коэффициент вариации V(Х):

(1.8)

Все эти величины (дисперсия, среднее квадратическое отклонение, коэффициент вариации) являются мерой разброса значений СВ относительно среднего значения.

Характеристики рассеяния значений СВ обычно применяются при изучении риска различных действий со случайным исходом: в финансовом анализе при оценивании различных активов и портфеля активов, при анализе риска инвестирования.

Например, если сравнивают две случайные величины, то та СВ, которая имеет большую дисперсию и среднее квадратическое отклонение, более вариабельна (изменчива). Риск, ассоциируемый с инвестициями, часто измеряют стандартным отклонением возврата инвестиций. Если сравниваются два типа инвестиций с одинаковой ожидаемой средней величиной возврата, то инвестиции с более высоким средним квадратическим отклонением считаются более рискованными (хотя более высокое стандартное отклонение предполагает более вариабельный возврат с обеих сторон - как ниже, так и выше средней).

Модой дискретной СВ называется ее наиболее вероятное значение.

Геометрическая интерпретация моды: мода - это абсцисса той точки полигона распределения, у которой ордината максимальна

Определение функции распределения для дискретной СВ:

Функцией распределения СВ Х называется функция F(x), которая определяется следующим образом:

, (1.9)

То есть это вероятность того, что СВ Х принимает значение меньшее, чем фиксированное действительное число X. При изменении значения Х Изменяются вероятности, поэтому функцию F(x) рассматривают как функцию переменной величины.

Согласно определению функции распределения (1.9), имеем следующие соотношения:

, (1.10)

Т. е. суммирование распространяется на все значения индекса I, Для которых ХI < X.

С учетом этого, функцию распределения F(x) для дискретной СВ, принимающей конечное число значений (табл.1.1), можно записать в следующем виде:

(1.11)

График функции F(x) Дискретной случайной величины - прерывистая ступенчатая линия.

Отметим некоторые важнейшие свойства F(x):

    1. Область значений (изменения) функции. 2. F(x) - неубывающая функция, то есть:

.

.

3. F(x) - функция непрерывная слева, т. е.

4. Если СВ Х принимает значения на отрезке [б, в], то

(1.12)

Эти свойства (кроме свойства 4) справедливы и для Непрерывной СВ.

Соотношение (1.12) используют для вычисления вероятности - вероятности события, при котором случайная величина принимает значения большие или равные А, Но меньшие B. Для дискретной СВ эту вероятность можно вычислить, используя непосредственно таблицу распределения, т. е. просто сложить соответствующие вероятности

.

Пример 1.1. Каждый урок учитель опрашивает у доски несколько учеников. Число опрошенных учеников зависит от многих факторов: планов на урок, сложности материала, уровня готовности учеников и т. д. Пусть X - число опрошенных учеников в определенный день. X - случайная величина, которая может быть только целым числом. Как показывает практика, число опрошенных учеников не превосходит 5. В нашем примере случайная величина X Принимает значения 0; 1; 2; 3; 4; 5, и вероятности этих значений равны 0,1; 0,2; 0,3; 0,2; 0,1; 0,1 соответственно (табл.1.2).

Таблица 1.2. Ряд распределения случайной величины X

Xi

0

1

2

3

4

5

P(xi)= pi

0,1

0,2

0,3

0,2

0,1

0,1

Поскольку появление различных значений случайной величины X - несовместные события, то вероятность того, что число опрошенных на уроке учеников равно 2 или 3, равна сумме вероятностей этих значений СВ Х (по теореме сложения вероятностей). Тогда P(Х=2 или Х=3) = P(Х=2) + P(Х=3) = 0,3 + 0,2 = 0,5.

Вероятность того, что число опрошенных на уроке учеников будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, т. к. P(1?X?4) = P(Х=1) + P(Х=2)+ P(Х=3) + P(Х=4) = 0,8. Вероятность того ни один ученик не будет опрошен P(X = 0) = 0,1.

Задание:

    1). Построить многоугольник (или полигон) распределения СВ X - числа опрошенных учеников. 2). Построить функцию распределения СВ X числа опрошенных учеников. 3). Используя функцию распределения, найти вероятность того, что число опрошенных на уроке учеников будет не меньше одного, но меньше трех, т. е. Р(1 ? Х < 3).

Решение.

1) Построение многоугольника (полигона) распределения СВ X - число опрошенных на уроке учеников приведено на рис. 1.1.

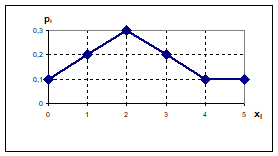
полигон распределения для данных примера 1.1

Рис. 1.1. Полигон распределения для данных примера 1.1

2) Построение F(Х) - функции распределения СВ X - числа опрошенных на уроке учеников. По определению:

.

Как следует из табл.1.2. случайная величина Х Не принимает значений, меньших 0. Следовательно, если Х < 0, то событие X < х Невозможно, а вероятность его равна нулю. Для всех значений Х, Удовлетворяющих двойному неравенству 0 ? x < 1, функция F(Х) означает вероятность события X < 1. Но случайная величина X Принимает значение меньшее 1 лишь в одном случае: значение 0 с вероятностью 0,1.

Если значение Х Удовлетворяет двойному неравенству, 0 ? Х < 2, то F(Х) = P(Х=0) + P(Х=1) = 0,1 + 0,2 = 0,3.

Пусть, например, Х = 2. Тогда F(2) есть вероятность события X < 2. Это событие возможно в двух случаях: случайная величина X принимает значение 0 (с вероятностью 0,1), или 1 (с вероятностью 0,2). Применив теорему сложения вероятностей, получим F(2) = P(Х=0 и Х=1) = 0,1 + 0,2 = 0,3. Аналогичные рассуждения позволяют найти функцию распределения для данных табл. 1.1. Результат приведен в табл. 1.3.

Функция распределения (интегральная функция распределения) для примера 1.1 приведена в таблице 1.3.

Таблица 1.3

X

F(х)

0

0,1

0,3

0,6

0,8

0,9

1,0

На рис. 1.2. представлен график функции распределения F(X). Функция распределения F(X)- неубывающая функция, ее значение равно единице при Х, Большем наибольшего возможного значения случайной величины или равном ему (рис. 1.2).

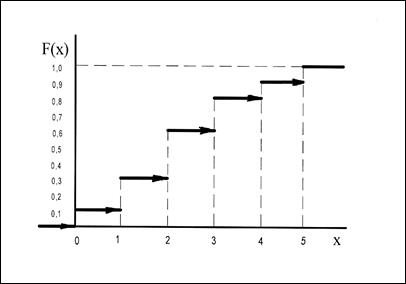
график функции распределения f(x)

Рис. 1.2. График функции распределения F(x)

График F(X) имеет ступенчатый вид. Функция распределения каждой дискретной случайной величины постоянна на интервалах и имеет скачки на границах, соответствующих значениям СВ. Величина скачков равна вероятностям конкретныx значений СВ (табл. 1.3).

3). Как следует из таблиц 1.2. и 1.3, вероятность того, что число опрошенных на уроке учеников в определенный день будет меньше трех, можно найти по формуле Р(Х < 3) = F(3) = 0,6. С другой стороны, эту же вероятность можно найти. используя по теорему сложения вероятностей:

Р(Х < 3) = P(Х=0 или Х=1 или Х=2) = 0,1 + 0,2 + 0,3 = 0,6.

Вероятность того, что на уроке будет опрошено не менее одного ученика, когда вероятность события X ? 1 вычисляется по формуле:

P(X ? 1) = 1-P(X < 1) = 1-0,1 = 0,9.

Где P(X < 1) вероятность того, что на уроке будет опрошено менее одного ученика, т. е. не будет опрошен ни один ученик. Вероятность события P(X ? 1) также можно найти по формуле:

P(X ? 1) = 1-P(X < 1) = 1-F(1) = 1-0,1 = 0,9.

Вероятность того, что число опрошенных учеников в определенный день будет не меньше одного, но меньше трех, можно найти по формуле Р(1 ? Х <3) = F(3)- F(1) = 0,6-0,1 = 0,5.

Этот же результат может быть получен непосредственно по ряду распределения СВ Х (табл.1.2):

Р(1 ? Х <3)=P(X=1)+P(X=2)=0,2+0,3=0,5.

Похожие статьи




Лабораторная работа 1. Вычисление числовых характеристик дискретной случайной величины, Базовые понятия - Элементы теории вероятностей и математической статистики

Предыдущая | Следующая