Вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события при этой гипотезе. - Случайные величины
применяем 2е теоремы:
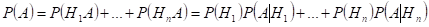
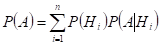
-формула полной вероятности
Теорема гипотез (формула Байеса).
Пусть вероятность полной группы не совместных гипотез H1, H2, ..., Hn известны и равны P(H1), P(H2), ..., P(Hn). Событие А может появиться совместно с условной вероятностью P(A|Hi) (i=1,2,...,n).
Спрашивается, как следует изменить вероятности гипотез после проведения опытов в связи с появлением этого события. Иными словами, требуется найти условную вероятность P(Hi, A).
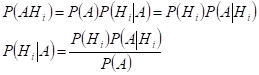
Формула Байеса:
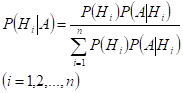
Ответ на билет 7
Числовые характеристики случайных величин.
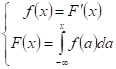
Закон распределения случайных величин, представленный в той или иной форме, дает исчерпывающее описание случайной величины. Наиболее существенные особенности распределения в компактной форме описываются так называемыми числовыми характеристиками случайных величин. Они играют в теории вероятности огромную роль, с их помощью облегчается решение вероятностных задач. Рассмотрим наиболее часто встречающиеся числовые характеристики.
Характеристики положения.
Мат. Ожидание Мода Медиана
Важнейшая характеристика математическое ожидание, которая показывает среднее значение случайной величины.
Математическое ожидание величины Х обозначается М[X], или mx.
Для дискретных случайных величин математическое ожидание:
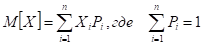
Сумма значений соответствующего значения на вероятность случайных величин.
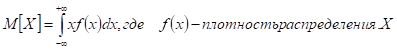
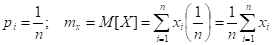
Модой (Mod) случайной величины Х называют ее наиболее вероятное значение.
Для дискретной случайной величины. Для непрерывной случайной величины.
Mod=X3 Mod=X0
Одномодальное распределение
Много модальное распределение
В общем случае Mod и математическое ожидание не совпадают.
Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один.
Med разделяет площадь под кривой на 2 равные части. В случае одномодального и симметричного распределения
Mx=Mod=Med
Моменты
Чаще всего на практике применяются моменты двух видов начальное и центральное.
Начальный момент. - го порядка дискретной случайной величины Х называется сумма вида:
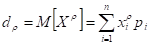
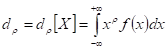
Для непрерывной случайной величины Х начальным моментом порядка называется интеграл, очевидно, что математическое ожидание случайной величины есть первый начальный момент.
Пользуясь знаком (оператором) М, начальный момент - го порядка можно представить как мат. ожидание - ой степени некоторой случайной величины.
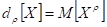
Центрированной случайной величиной соответственной случайной величины Х называют отклонение случайной величины Х от ее математического ожидания:
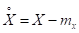
Математическое ожидание центрированной случайной величины равно 0.
Для дискретных случайных величин имеем:
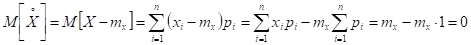
Моменты центрированной случайной величины носят название Центральных моментов
Центральный момент порядка случайной величины Х называют математическим ожиданием - ой степени соответствующей центрированной случайной величины.
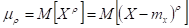
Для дискретных случайных величин:
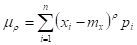
Для непрерывных случайных величин:
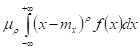
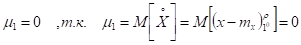
Связь между центральными и начальными моментами различных порядков
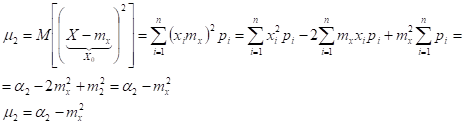
Из всех моментов в качестве характеристики случайной величины чаще всего применяют первый момент (мат. ожидание) и второй центральный момент.
Второй центральный момент называют дисперсией случайной величины. Он имеет обозначение:
Согласно определению
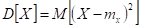
Для дискретной случайной величины:
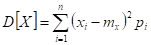
Для непрерывной случайной величины:
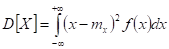
Дисперсия случайной величины есть характеристика рассеянности (разбросанности) случайных величин Х около ее математического ожидания.
Дисперсия означает рассеивание. Дисперсия имеет размерность квадрата случайной величины.
Для наглядной характеристики рассеивания удобнее использовать величину, my той, что и размерность случайной величины. С этой целью из дисперсии извлекают корень и получают величину, называемую - среднеквадратичным отклонением (СКО) случайной величины Х, при этом вводят обозначение:
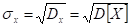
Среднеквадратичное отклонение иногда называют "стандартом" случайной величины Х.
Итак:
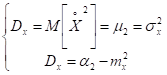
Математическое ожидание mx и Dx (или СКО ) наиболее частые употребляемые характеристики случайных величин, так как они определяют наиболее важные черты распределения, его положения и степень разбросанности.
Ответ на билет 9
Равномерное распределение
Равномерная плотность распределения определяется следующим образом:
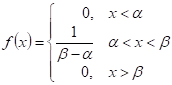
Функция распределения определяется:
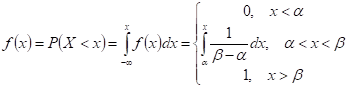
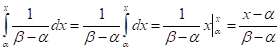
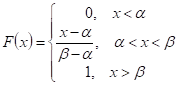
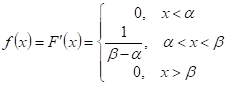
Найдем числовые характеристики:
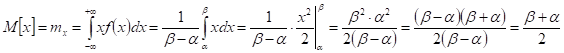
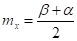
(математическое ожидание)
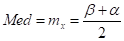
(медиана), Mod - не существует для данного распределения
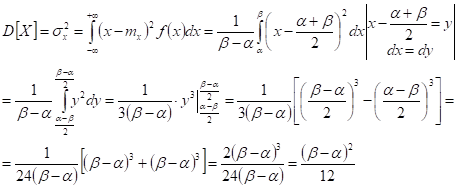
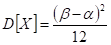
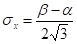
(дисперсия), (среднеквадратичное отклонение)
Ответ на билет 10
Закон распределения Пуасона
Рассмотрим дискретную случайную величину х, имеющую ряд распределения:
|
X |
X0=0 |
X1=1 |
... |
Xm=m |
... |
|
P |
P0 |
P1 |
... |
Pm |
... |
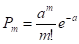
Говорят, что данное случайное распределение подчинено закону распределения Пуасона.
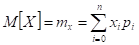
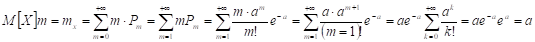
(k=m-1)
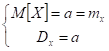
Ответ на билет 11
Нормальный закон распределения (закон Гауса)
Главная особенность в том, что он является предельным законом, к которому приближаются другие распределения, при весьма часто встречающихся типичных условиях.
Нормальный закон распределения характеризуется плотностью вероятности вида:
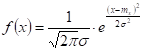
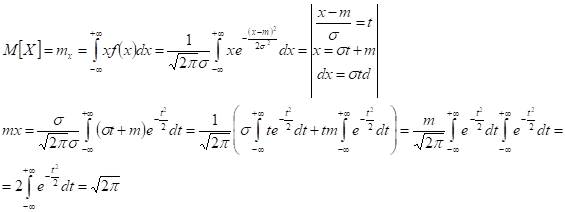
Можно показать, что дисперсия
Ответ на билет 13
Независимые случайные величины.
Случайные величины x и y независимы если вероятность.
Для зависимых величин x и y вероятность
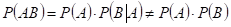
Корреляционным моментом или Ковариацией случайных величин x и y называют величину:
Можно показать, что для независимых случайных величин cov(x, y)=0
Коэффициент корреляций
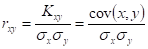
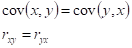
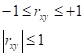
Случайные величины x1, x2, x3, ..., xn, называются не коррелированными, если
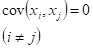
Ответ на билет 14
Теорема о числовых характеристиках
Если c не случайная (детерминированная) величина, то M[c]=c и D[c]=0
Если c не случайная - постоянная, а Х случайная (детерминированная), то:
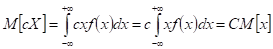
Математическое ожидание суммы нескольких величин равно сумме их ожиданий.
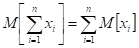
Математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов.
Похожие статьи
-
Обозначим вероятность соответствующих событий через Pi - Случайные величины
, Так как рассматриваемые события образуют полную группу не совместных событий, то Х полностью описана с вероятностной точки зрения, если мы зададим...
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин
Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится. Не будет лишним помнить, что этот...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Односторонние и двухсторонние значения вероятностей - Распределение вероятности случайных величин
Если нам известен закон распределения СВ (пусть - дискретной), то в этом случае очень часто приходится решать задачи, по крайней мере, трех стандартных...
-
Нормальное распределение - Распределение вероятности случайных величин
Первым, фундаментальным по значимости, является т. н. Нормальный закон Распределения непрерывной случайной величины X, для которой допустимым является...
-
Математическое ожидание генеральной совокупности назовем генеральной средней, т. е. . Теорема. Выборочное среднее есть состоятельная и несмещенная оценка...
-
Законы распределений дискретных случайных величин. - Распределение вероятности случайных величин
Пусть некоторая СВ является дискретной, т. е. может принимать лишь фиксированные (на некоторой шкале) значения X I. В этом случае ряд значений...
-
Непрерывные величины - возможные значение, которых непрерывно заполняют некоторый диапазон. Плотность распределения вероятности непрерывной случайной...
-
Распределения непрерывных случайных величин - Распределение вероятности случайных величин
До этого момента мы ограничивались только одной "разновидностью" СВ - дискретными, т. е. принимающими конечные, заранее оговоренные значения на любой из...
-
Вопросы по теории вероятностей - Случайные величины
Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. Сумма и произведение событий, теоремы сложения и...
-
Шкалирование случайных величин - Распределение вероятности случайных величин
Как уже отмечалось, дискретной называют величину, которая может принимать одно из счетного множества так называемых "допустимых" значений. Примеров...
-
Контрольная работа По дисциплине: Теория вероятностей Контрольная работа № 1 Вариант 1 Задача № 1 Условие: Из 10 изделий, среди которых 4 бракованные,...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
Статистическая вероятность и распределения случайных величин - Основы научных исследований
В теории вероятностей под случайной величиной понимают отношения числа благоприятных исходов испытаний к общему числу испытаний. Например, если из 10...
-
В общем случае: , где Для не корреляционных случайных величин: Ответ на билет 15 В широком смысле слова, закон больших чисел характеризует устойчивость...
-
Большую роль в теории и практике системного анализа играют некоторые стандартные распределения непрерывных и дискретных СВ. Эти распределения иногда...
-
Пусть у нас имеется некоторая непрерывная случайная величина X, распределенная нормально с математическим ожиданием и среднеквадратичным отклонением....
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Случайные события и случайные величины - Основы научных исследований
Вероятностные закономерности проявляются только в массовых явлениях, т. е. когда один и тот же объект изменяет свое состояние многократно или когда...
-
Генеральная и выборочная совокупности Для обнаружения закономерностей, описывающих исследуемое массовое явление, необходимо иметь опытные данные,...
-
Вариационные ряды - Математическое ожидание случайной величины
После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине - т. е....
-
Введение - Математическое ожидание случайной величины
Математическая статистика - наука, изучающая методы исследования закономерностей в массовых случайных явлениях и процессах по данным, полученным из...
-
Дисперсия - Основы научных исследований
Степень рассеивания случайной величины относительно центра распределения характеризуется Дисперсией (от лат. dispersio - рассеивание). Дисперсия - это...
-
Математическое ожидание - Основы научных исследований
Интегральная и дифференциальная функции распределения являются исчерпывающими статистическими характеристиками любой случайной величины. Однако многие...
-
Выборочные распределения на шкалах Int и Rel
Оценка наблюдений при неизвестном законе распределения Какова цель наблюдений над случайной величиной; для чего используются результаты наблюдений; где,...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Введение - Проверка статистических гипотез
Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое...
-
ТВ-раздел математики, в которой используются различные разделы математики для своего развития. Задача: выяснение закономерностей, возникающих при...
-
Асимметрия и эксцесс - Основы научных исследований
Количественно степень несимметричности распределения оценивается при помощи одной из мер этого параметра - Асимметрией , Где М3 - центральный момент...
-
Параметры эмпирических распределений - Основы научных исследований
По опытным (эмпирическим) данным строятся распределения исследуемых случайных величин. Функции плотности Р(х) таких распределений могут иметь один...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Пусть требуется разыграть испытания в каждом из которых событие А появляется с вероятностью р и не появляется с вероятностью 1-р [4]. Заменим...
-
Проверка статистических гипотез - Основы научных исследований
Для проверки статистических гипотез используются статистики, называемые статистическими критериями или иначе - критериями значимости. В частности, для...
-
Проверка гипотез о законе распределения, Критерий К. Пирсона - Проверка статистических гипотез
Критерий К. Пирсона Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим...
-
Взаимосвязи случайных событий - Закон распределения случайной величины
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти)....
-
Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели
Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...
-
Метод максимального правдоподобия - Основы научных исследований
Разработан Р. Фишером. Пусть Х 1 ,х 2 ...х N - выборка из генеральной совокупности случайной величины Х с функцией плотности вероятности Р(х, и),...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
Вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события при этой гипотезе. - Случайные величины