Задание 2. "Прогнозирование на основе тренда временного ряда" - Методы прогнозирования в экономической статистике

Необходимо провести прогноз товарооборота магазина "Ткани для дома" на тринадцатый день.

Исходные данные:

Таблица 2.1 - Ежедневный товарооборот магазина "Ткани для дома" тыс. руб.

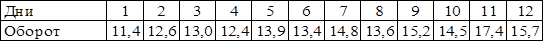
Для выявления наличия тенденции в ряду, построим график по исходным данным (таблица 2.1) и проведем визуальный анализ.

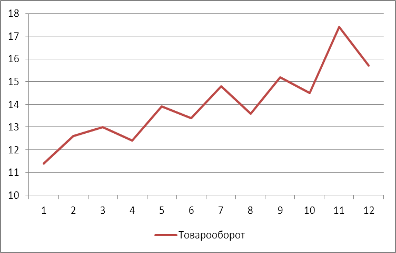
Рисунок 2.1 - Ежедневный товарооборот магазина "Ткани для дома"

Визуальный анализ графика (рисунок 2.1) позволяет сделать предварительный вывод о том, что временной ряд содержит тенденцию среднего уровня ряда - возрастающий тренд и он, предположительно - линейный, так как оборот, хотя и колеблется, но в среднем, увеличивается во времени.

Чтобы полученная визуальная оценка была более убедительной и наглядной, осуществим сглаживание временного ряда с помощью метода скользящей средней с интервалом сглаживания, равным трем.

Рассчитаем сглаженные уровни ряда по формуле:

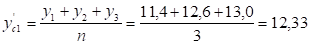
Построим график товарооборота по фактическим и сглаженным данным.

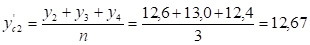
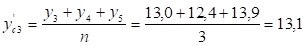
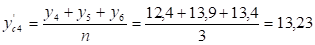
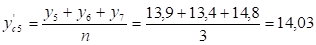
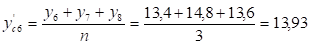
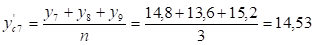
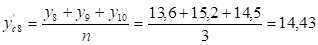
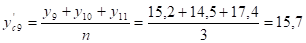
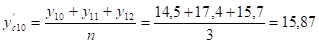
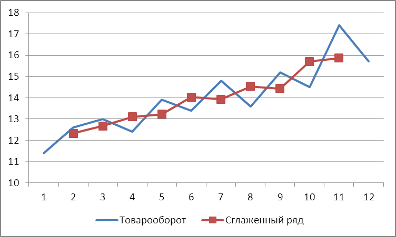
Рисунок 2.2 - Ежедневный товарооборот магазина "Ткани для дома" путем метода сглаживания

Визуальный анализ графиков оборота по фактическим и сглаженным данным (рисунок 2.2) позволяет убедиться в правильности сделанного ранее вывода о наличии в ряде тенденции. Сглаженная кривая постоянно возрастает. Оценим наличие тенденции в виде тренда и дисперсии в исходном временном ряде с помощью метода Фостера - Стюарта.

Для реализации этого метода вначале определим uT и lT:

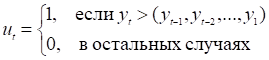
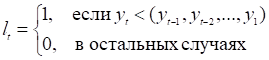
Таблица 2.2

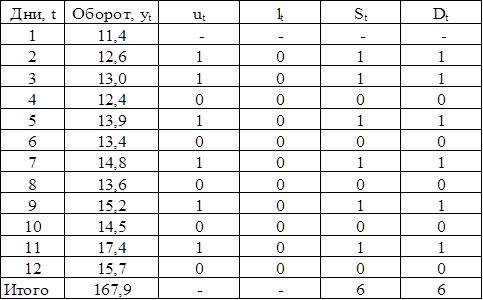
Затем, на основе величин uT и lT, определим величины S и D:

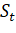
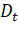
S = ?, где = uT + lT, D = ?, где = uT - lT

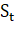
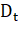
Величина S используется для оценки наличия в ряде тенденции дисперсии, а величина D - для оценки наличия тенденции среднего уровня.

Выдвинем нулевую гипотезу: во временном ряде нет тенденции среднего уровня и нет тенденции дисперсии.

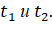
Для проверки выдвинутой нулевой гипотезы необходимо рассчитать значения Для этого надо знать значения м, у1, у2 ([1], приложение 2, стр.41). Найдем м для n = 12:

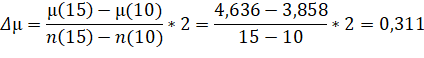
Отсюда м (12) = м (10) + Дм = 3,858 + 0,311 = 4,169. Аналогичным образом найдем значения для у1 (12) = 1,381 и для у2 (12) = 2,04 ([1], приложение 2, стр.41).

Найдем значения t1 и t2:

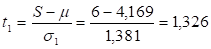
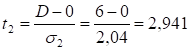
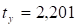
Теперь найдем табличное значение t. Для этого зададимся уровнем значимости б = 0,05. Затем определим доверительную вероятность и число степеней свободы k = n-1 = 12 - 1 = 11. Относительно найденных значений и k по таблице "Значение t-критерия Стьюдента" ([1], приложение 2, стр.41). Табличное значение.

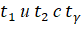
Сопоставим значения.

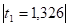
Постольку <, постольку нулевая гипотеза о том, что во временном ряде отсутствует тенденция дисперсии, принимается.

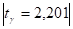
Поскольку >, постольку нулевая гипотеза о том, что во временном ряде отсутствует тенденция среднего уровня отвергается. Отсюда с вероятностью б = 0,05 (5%) можно утверждать, что во временном ряде имеет место тенденция среднего уровня.

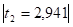
Так как наши визуальные и аналитические оценки совпали, то с высокой степенью вероятности можно считать, что во временном ряде имеет место тенденция среднего уровня, а тенденция дисперсии отсутствует.

Оценим наличие тенденции в виде тренда в исходном временном ряде с помощью коэффициента Кендэла (коэффициента ранговой корреляции).

Расчет проведем с помощью таблицы 2.3

Таблица 2.3 - Расчет числа случаев превышения текущим уровня ряда, предыдущих ему уровней ряда

Месяц	Оборот
1	2	3
1	11,4	-
2	12,6	1
3	13,0	2
4	12,4	1
5	13,9	4
6	13,4	4
7	14,8	6
8	13,6	5
9	15,2	8
10	14,5	7
11	17,4	10
12	15,7	10
Итого:	167,9	58

Первый уровень ряда не с чем сравнить (нет предыдущих уровней ряда), поэтому в третьей графе мы поставим прочерк. Второй уровень ряда больше предыдущего, поэтому в графе 3 ставим 1. Третий уровень ряда больше двух предыдущих, поэтому в графе 3 ставим 2. Четвертый уровень больше одного предыдущего, поэтому в графе 3 ставим 1. Аналогичным образом определим число таких случаев и для остальных уровней ряда.

Подведем итог по графе 3 таблицы 2.3, найдем общее число случаев, когда текущий уровень ряда больше предыдущих, он равен 58.

Определим расчетное значение коэффициента Кендэла:

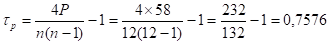
Рассчитаем теоретическую дисперсию:

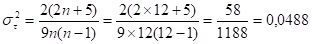
Для оценки наличия в ряде тенденции среднего уровня ряда выберем вероятность, равную 0,95 (95%). С учетом выбранной вероятности коэффициент доверия t = 1,96.

При сопоставлении может возникнуть три варианта:

Первый вариант, когда с вероятностью T во временном ряде нет тренда;

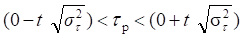
Где T - Коэффициент доверия. При выбранной вероятности 0,68 (68%) он равен единице, при выбранной вероятности 0,95 (95%) он равен 1,96.

Второй вариант, когда с вероятностью T во временном ряде есть убывающая тенденция среднего уровня ряда;

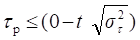
Третий вариант, когда с вероятностью - T во временном ряде есть возрастающая тенденция среднего уровня ряда.

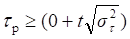
Сопоставим расчетное и теоретическое значения коэффициента Кендэла.

Из трех вариантов выбираем третий, поскольку только в нем выполняется необходимое соотношение расчетного и теоретического значений коэффициентов Кендэла, т. е.

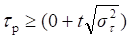
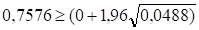
Из установленного соотношения следует, что с вероятностью 95% во временном ряде есть возрастающая тенденция среднего уровня ряда. Этот вывод согласуется с выводами, полученными ранее при визуальном анализе графиков временного ряда и применении метода Фостера - Стюарта.

Определим трендовые модели

Трендовая модель - это уравнение тренда. Модели могут классифицироваться по следующим основным признакам:

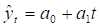
По форме взаимодействия элементов модели подразделяются на аддитивные и мультипликативные.

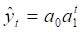
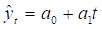
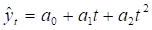
По характеру взаимодействия фактора t и зависимой переменной yT модели подразделяются на линейные и нелинейные.

Визуальный анализ графика (рисунок 2.1) позволил сделать предварительный вывод о том, что временной ряд содержит тенденцию среднего уровня ряда - возрастающий тренд и он, предположительно - линейный, так как оборот, хотя и колеблется, но в среднем, увеличивается во времени.

Чтобы приблизительно оценить, соответствуют ли динамика изменений исходных данных линейному тренду, необходимо рассчитать абсолютный цепной прирост уровней временного ряда ?T или разности первого порядка, что одно и то же, т. е.

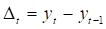
Или

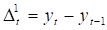
Данные расчетов занесем в таблицу 2.4

Таблица 2.4 - Абсолютный цепной прирост.

Уровень временного ряда	11,4	12,6	13,0	12,4	13,9	13,4	14,8	13,6	15,2	14,5	17,4	15,7
Абсолютный цепной прирост	-	+1,2	+0,4	-0,6	+1,5	-0,5	+1,4	-0,8	+1,6	-0,7	+2,9	-1,7

Анализ второй строки таблицы 2.4 показывает, что прирост относительно постоянен по абсолютной величине. Это дает возможность предположить, что для описания исходных данных можно использовать линейный тренд.

Проверим, можно ли описать изменения данных с помощью параболы второго порядка. Для этого используем таблицу 2.4, дополнив ее третьей строкой, в которую внесем разности второго порядка.

Рассчитаем разность второго порядка по абсолютной величине:

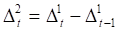
Таблица - 2.5

Уровень временного ряда	11,4	12,6	13,0	12,4	13,9	13,4	14,8	13,6	15,2	14,5	17,4	15,7
Абсолютный цепной прирост	-	+1,2	+0,4	-0,6	+1,5	-0,5	+1,4	-0,8	+1,6	-0,7	+2,9	-1,7
Разности второго порядка	-	-	-0,8	-1,0	+2,1	-2,0	+1,9	-2,2	+2,4	-2,3	+3,6	-4,6

Анализ третьей строки таблицы 2.5 показывает, что разности второго порядка по абсолютной величине относительно не постоянны. Это позволяет предположить, что для описания исходных данных не может быть использована парабола. Сложившиеся ситуация таблица 2.4 и 2.5, когда на предварительном этапе выбора трендовой модели выясняется, что необходимо использовать специальные оценочные критерии, с помощью которых и осуществляется выбор наилучшей трендовой модели.

Рассмотрим возможность использования степенного тренда для описания исходных данных (таблица 2.1), рассчитав цепные темпы роста в таблице 2.6

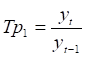
Таблица 2.6

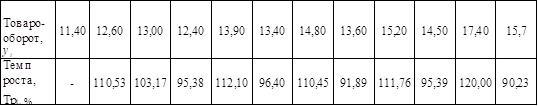
Анализ второй строки таблицы 2.6 показывает, что по мере возрастания объема товарооборота остается относительно постоянным. Это позволяет предположить, что для описания исходных данных использование степенного тренда менее предпочтительно, чем показательный тренд.

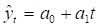
Проверим параметры линейного тренда методом усреднения по левой и правой половине.

Разделим данные таблицы (таблица 2.1) на две части. Поскольку данные представлены за 12 дней (четное число), постольку в первую часть попадут данные с 1-го по 6-й день работы, а во вторую часть - с 7-го по 12-й день работы. Рассчитаем по каждой половине среднее число дней и средние объемы продаж.

Для первой половины данных:

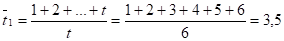
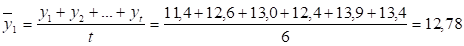
Для второй половины данных:

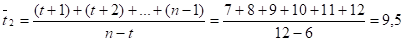
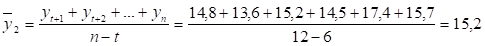
В результате расчетов получили координаты двух точек А (3,5; 12,78) и В (9,5; 15,2). В прямоугольной системе координат (рисунок 2.3) построим эти точки. Через них проведем прямую до пересечения с осью ординат (объем продаж).

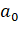
Точка пересечения построенной прямой и оси дает значение ; в данном случае.

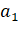
Теперь определим значение параметра. Для расчета выберем время

=2,5. Выбранному времени =2,5 соответствует объем продаж =12,8.

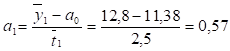
В результате расчетов выбранная линейная модель yбудет иметь следующий конкретный вид y.

Найдем параметры линейного тренда с помощью метода наименьших квадратов (МНК).

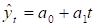
Для расчета параметров линейного тренда методом МНК используем данные табл. 2.1 Для проведения промежуточных расчетов построим таблицу 2.7, и проведем в ней необходимые расчеты.

Таблица 2.7

T	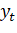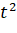Ty
1	11,4	1	11,4
2	12,6	4	25,2
3	13,0	9	39,0
4	12,4	16	49,6
5	13,9	25	69,5
6	13,4	36	80,4
7	14,8	49	103,6
8	13,6	64	108,8
9	15,2	81	136,8
10	14,5	100	145,0
11	17,4	121	191,4
12	15,7	144	188,4
78	167,9	650	1149,1

Найдем параметры :

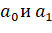
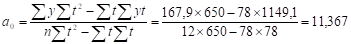
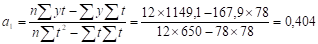
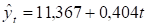
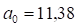
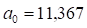
В результате расчетов линейный тренд будет иметь следующий конкретный вид. Сравним параметры линейного тренда, вычисленные графическим методом - и и методом МНК - и. Они достаточно близки.

Построим графики исходного ряда и выбранного линейного тренда (рисунок 2.3) и визуально оценим совпадение линейного тренда и реального тренда временного ряда, который может иметь место во временном ряде.

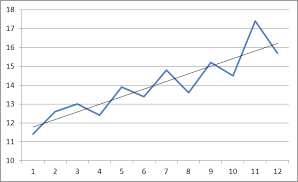
Рисунок 2.3 - Линейный тренд

Визуальный анализ позволяет говорить о том, что выбранный линейный тренд совпадает с реальным трендом временного ряда.

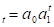
Рассчитаем параметры для показательного тренда y. Найти их методом МНК невозможно, так как этот тип тренда нелинейный. Чтобы обойти этот сдерживающий момент, осуществим линеаризацию (выравнивание) показательного тренда с помощью десятичного или натурального логарифма. Выберем натуральный логарифм.

В результате логарифмирования исходная трендовая модель будет выглядеть следующим образом:

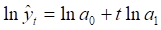
В линеаризированной модели показательного тренда параметрами будут и. Вот их значения уже можно найти методом МНК, построив видоизмененную систему линейных уравнений

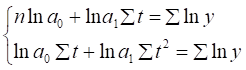
В результате решения этой системы уравнений найдем параметры линеаризированной модели показательного тренда.

С помощью табл.2.7 рассчитаем необходимые промежуточные данные.

Таблица 2.8

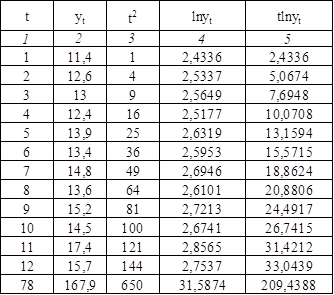
На основе данных итоговой строки табл.2.8 определим параметры линеаризированной модели показательного тренда и :

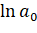
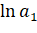
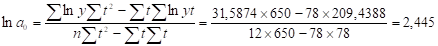
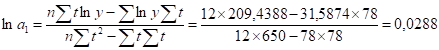
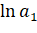
Найдем значения и, пропотенцировав и. Тогда:

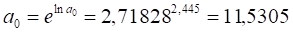
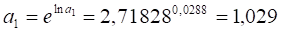
В результате расчетов параметров показательный тренд будет иметь следующий конкретный вид: yT =11,5305 х 1,029T.

Данные можно описать с помощью линейного и показательного трендов. Расчеты дали конкретные значения этих трендов:

yT =11,367+0,404t и yT =11,5305 х 1,029T

Выбранные тренды имеют одинаковое число параметров (по два), поэтому для расчета критерия наименьшей суммы квадратов отклонений выберем формулу:

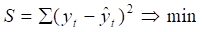
Оценим степени апроксимации выбранной трендовой модели.

Апроксимация (приближение) - это замена исходных данных наиболее близкими к ним другими данными, представленными в виде тренда.

Расчеты, проведенные выше, дали конкретные значения этих трендов:

yT =11,367+0,404t и yT =11,5305 х 1,029T

Для проведения промежуточных расчетов построим таблицу 2.9.

Таблица 2.9

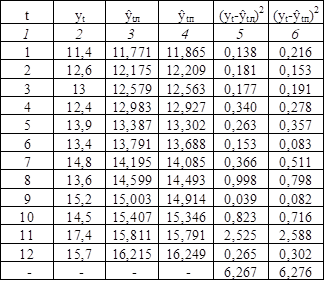
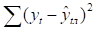
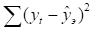
Сравним значения критерия наименьшей суммы квадратов отклонений для линейного и показательного трендов. Для линейного тренда критерий равен 6,267 (), а для показательного - 6,276 (). Коэффициент для линейного тренда меньше, чем для показательного, поэтому линейный тренд лучше аппроксимирует исходные данные. Следовательно, для прогнозирования необходимо взять линейный тренд.

Для линейного тренда рассчитаем величину и построим ее график. Оценим адекватность линейного тренда.

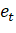
Чтобы оценить адекватность выбранной трендовой модели теоретическому тренду временного ряда, найдем разность между исходными данными и нашей трендовой моделью :

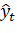
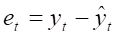
Для проведения расчетов построим таблицу 2.10, используя данные таблицы 2.9

Таблица 2.10

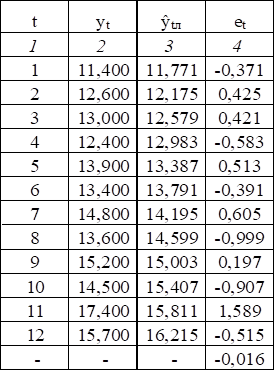
По данным таблицы 2.10 построим график величины еT.

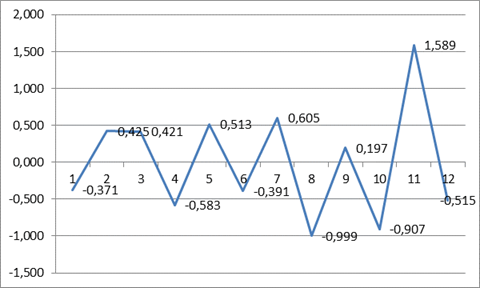
Рисунок 2.4 - График величины еt

Проверим, носит ли колебание величины еT случайный характер. Это условие означает, что колебание (изменение) величины еT не содержит элементов тенденции.

Для получения утвердительного ответа необходимо, чтобы величина еT отвечала следующим четырем условиям (требованиям).

Условие 1. Колебание величины еT должно носить случайный характер.

Это условие означает, что колебание величины еT не содержит элементов тенденции. Проверим данное условие с помощью критерия поворотных точек.

Величина еT считается поворотной, если она соответствует одному из двух условий:

ЕT-1< еT> еT+1 или еT-1> еT< еT+1

Точку е1=-0,371 нельзя рассматривать в качестве поворотной, так как у нее нет предыдущего значения.

Точка е2 Является поворотной, так как - 0,371<0,425>0,421.

Точка е3 Не является поворотной, так как 0,425>0,421>-0,583.

Точка е4 Является поворотной, так как 0,421>-0,583<0,513.

Точка е5 Не является поворотной, так как - 0,583>0,513>-0,391

Точка е6 Является поворотной, так как 0,513>-0,391<0,605

Точка е7 Является поворотной, так как - 0,391<0,605>-0,999

Точка е8 Является поворотной, так как 0,605>-0,999<0, 197

Точка е9 Является поворотной, так как - 0,999<0, 197>-0,907

Точка е10 Является поворотной, так как 0, 197>-0,907<1,589

Точка е11 Является поворотной, так как - 0,907<1,589>-0,515

Следовательно, не выполняется ни одно из условий.

Рассматриваемые точки обозначим РT. Тем точкам, которые будут поворотными, присвоим значение РT. =1. А тем точкам, которые не будут поворотными, присвоим значение РT. =0.

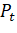
Рассматриваемые точки обозначим и занесем в таблицу 2.11.

Таблица 2.11

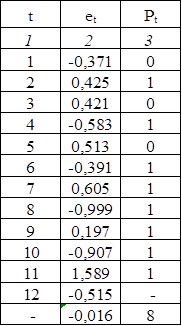
Затем определим общее число поворотных точек в ряде еT, их 8, т. е.:

Р=У РT=8

Для проверки выполнения условия 1 выдвинем нулевую гипотезу Н0: Колебание величины носит случайный характер.

Чтобы проверить нулевую гипотезу, вначале определим математическое ожидание и дисперсию числа поворотных точек:

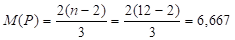
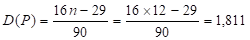
Для проверки нулевой гипотезы используем вероятность, равную 95%, которой соответствует коэффициент доверия t = 1,96.

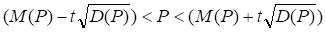
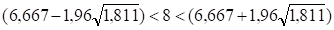
4,029<8<9,305

Следовательно, с вероятностью 0,95 (95%) можно утверждать, что колебание величины еT носит случайный характер и, следовательно, отвечает данному требованию.

Условие 2. Распределение величины et соответствует нормальному распределению.

Данное условие проверяется с помощью RS-критерия.

Проверим в табл. 2.12 распределение на соответствие нормальному распределению.

Таблица 2.12

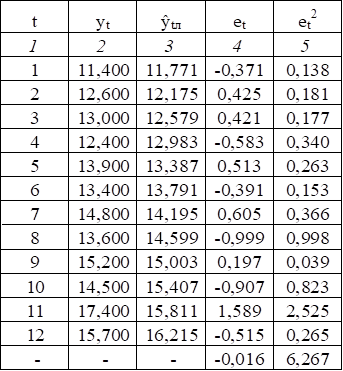
Вначале определим среднее квадратическое отклонение:

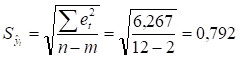
Рассчитаем расчетное значение критерия RSP, найдя предварительно в графе 4 таблицы 2.12 максимальное еMax=0,835 и минимальное еMin=-0,875 значения:

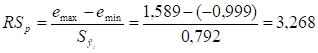
Следующим шагом проверки условия 2 является нахождение табличного значения RS-критерия - RSТ. В таблице "Значения RS-критерия для n = 10...30" ([1], приложение 3, стр.41) приводятся нижнее и верхнее значения RS-критерия для n = 10 и n = 20; а у нас n = 12. Для нахождения нижнего и верхнего значений RS-критерия для n = 12 используем линейную интерполяцию. В результате расчета нижнее значение RS12Н = 2,772, а верхнее - RS12В = 3,978.

Выдвинем нулевую гипотезу Н0: Величина соответствует нормальному распределению.

Сопоставим расчетное значение критерия RSР с табличным - RSТ:

RSNн<RSP<RSNв

2,772<3,268<3,978

Сопоставление показывает, что RSР попадает в интервал, определяемый нижним и верхним табличными значениями RS-критерия. Это позволяет сделать вывод, что с вероятностью 0,95 (95%) нулевая гипотеза принимается, т. е. величина соответствует нормальному распределению и, следовательно, отвечает условию 2.

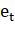
Условие 3. Математическое ожидание величины равно нулю.

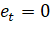
Для проверки данного условия выдвинем нулевую гипотезу Н0: MeT = 0, т. е. математическое ожидание.

Вначале определим среднюю арифметическую величину :

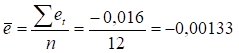
Затем рассчитаем и внесем в табл. 2.13 квадрат отклонения фактического значения от ее среднего значения.

Таблица 2.13

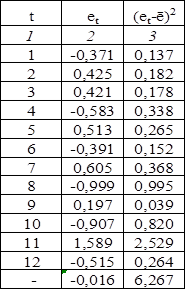
Далее определим среднее квадратическое отклонение:

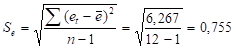
Теперь найдем расчетное значение tР

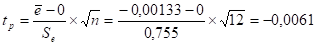
Найдем значение величины tТ по таблице "Значение t-критерия Стьюдента" ([1], приложение 2, стр. 41), зададимся уровнем значимости б = 0,05, относительно которого определим доверительную вероятность г = 1 - 0,05 = 0,95, а также число степеней свободы k = 12 - 1 = 11. теперь, зная г и k, определим tТ по Стьюденту; tТ = 2, 201. Сопоставим расчетное tР = - 0,0061 и табличное tТ = 2, 201 значения:

TP<tT Или - 0,0061 <2, 201

Сопоставление показывает, расчетное значение меньше табличного.

Это позволяет сделать следующий вывод: с вероятностью 0,95 (95%) нулевая гипотеза принимается, и мы можем утверждать: математическое ожидание.

Условие 4. Независимость членов ряда друг от друга.

Это условие означает отсутствие автокорреляции во временном ряде, т. е. взаимосвязи, в среднем, значения текущего уровня ряда от какого-то предыдущего. Наличие в ряде автокорреляции проверяется с помощью критерия Дарбина-Уотсона.

Вначале в табл.2.14 внесем квадраты разниц между текущим и предыдущим значениями.

Таблица 2.14

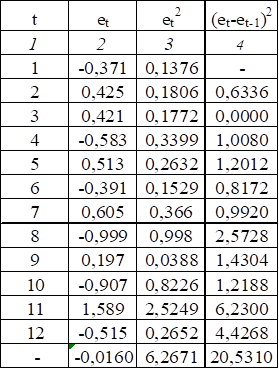
Определим расчетное значение критерия Дарбина-Уотсона :

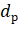
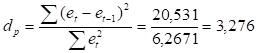
Расчетное значение критерия Дарбина-Уотсона оказалось больше двух, поэтому пересчитаем его для области с положительной корреляцией

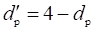
=4?3,276=0,724

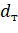
Найдем значение критерия Дарбина-Уотсона по таблице "Распределение критерия Дарбина-Уотсона для положительной автокорреляции (для 5% - го уровня значимости)" ([1], приложение 4, стр.42), при n = 12, и числе факторов в используемой трендовой модели V = 1.

Его нижнее значение равно d1=0,97, а верхнее d2=1,33. Сопоставим расчетное (0,724) и табличное (0,97; 1,36) значения критерия Дарбина-Уотсона. Видно, что расчетное значение меньше нижнего табличного, т. е. возникает первая ситуация, когда dР< d1 или 0,724<0,97. С учетом этого можно сделать вывод: с вероятностью 0,95 (95%) в ряде присутствует автокорреляция.

Рассчитаем точечную и интервальную оценку с периодом упреждения, равным ф = 1.

В табл. 2.1 приведен ежедневный оборот магазина "Ткани для дома" за 12 дней, он описан линейным трендом yT=11,367+0,404t.

Определим точечный и интервальный прогнозы на 13-й день.

Из условия задачи вытекает: период основания прогноза n = 12, а период упреждения прогноза ф = 1, уровень значимости б = 0,05.

Рассчитаем точечный прогноз

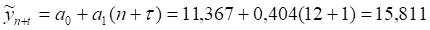
Тыс. руб.

Для расчета интервального прогноза предварительно определим табличное значение критерия Стьюдента с уровнем значимости б = 0,05 и числом степеней свободы k = n - 2 = 12 - 2 = 10. Табличное значение критерия Стьюдента tT=2,228.

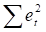
Затем находим стандартную ошибку тренда, взяв значение из табл. 2.14.

Стандартную ошибку тренда находим по формуле:

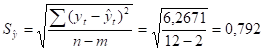
Теперь определим интервальный прогноз:

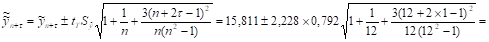
=15,811±2,072

Отсюда верхняя граница прогнозного интервала 15,811+2,072=17,883, а нижняя 15,811-2,072=13,739. Таким образом, прогноз оборота магазина "Ткани для дома" на 13-й день с вероятностью 0,95 (95%) будет расположена в интервале от 13,739 до 17,883 тыс. руб.

Интервальный прогноз можно найти иначе:

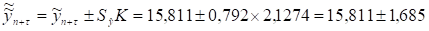
К - табличное значение ([1], приложение 6 "Значение K для оценки интервалов прогноза при вероятности г = 0,9 (линейный тренд)", стр.43), взятое с учетом того, что n = 12 и ф = 1.

Отсюда верхняя граница прогнозного интервала 15,811 + 1,685 = 17,496, а нижняя 15,811 - 1,685 = 14,126. Таким образом, прогноз оборота магазина "Ткани для дома" на 13-й день с вероятностью 0,9 (90%) будет расположена в интервале от 14,126 и 17,496 тыс. руб.

Задание 3. "Прогнозирование на основе сезонного цикла временного ряда"

Объем реализации продукции фирмы за три года приведен в таблице 3.1 Требуется определить прогнозный объем реализации продукции на декабрь 2008 г. с использованием мультипликативной модели временного ряда.

Таблица 3.1 - Объем реализации продукции фирмы АО "Лен" (руб.)

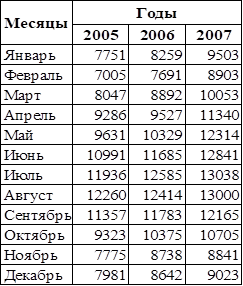
Таблица 3.2 - Варианты прогнозирования

Прогнозируемый месяц	Период упреждения прогноза, ф (год)	Модель ряда
Декабрь	1	Мультипликативная

Построим график по исходным данным и осуществим его визуальный анализ (Рис. 3.1).

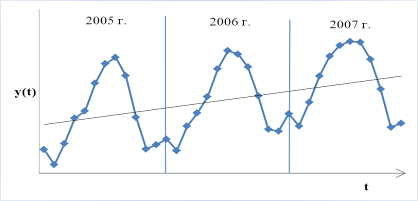
Рисунок 3.1 Объем реализации продукции фирмы АО "Лен" за 3 года.

Визуальный анализ графика позволяет сделать однозначный вывод о том, что временной ряд содержит сезонную компоненту, так как характер колебания ряда стабильно повторяется из года в год и имеет приблизительно одинаковый характер изменения.

Оценим наличие тенденции в виде тренда в исходном временном ряде с помощью коэффициента Кендэла.

Расчет проведем с помощью таблицы 3.3.

Таблица 3.3 - Расчет числа случаев превышения текущим уровня ряда, предыдущих ему уровней ряда

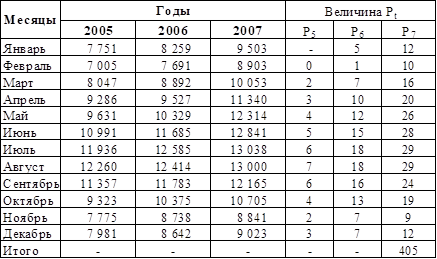
Общее число случаев, когда текущий уровень ряда больше предыдущих, равен - 405.

Определим расчетное значение коэффициента Кендэла:

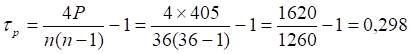
Рассчитаем теоретическую дисперсию:

Сопоставим расчетное и теоретическое значения коэффициента Кендэла.

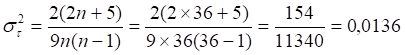
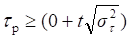
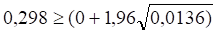
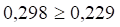
Из установленного соотношения следует, что с вероятностью 95% во временном ряде имеется возрастающая тенденция среднего уровня ряда.

На основе ранее полученных частных выводов можно сделать обобщенный вывод: во временном ряде с высокой степенью вероятности (95%) присутствует тенденция среднего уровня ряда и дисперсии.

Осуществим точечный прогноз сезонного цикла на основе линейной трендовой модели на декабрь 2008 года.

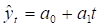
Для расчета параметров линейного тренда методом МНК используем данные табл. 3.1 Для проведения промежуточных расчетов построим таблицу 3.4, и проведем в ней необходимые расчеты.

Таблица 3.4

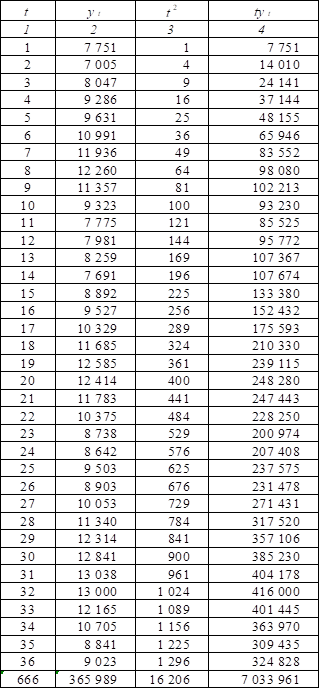
Найдем параметры :

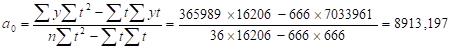
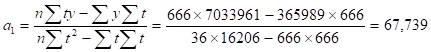
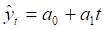
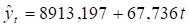
В результате расчетов линейный тренд будет иметь следующий конкретный вид.

Анализ временного ряда показал, что данные временного ряда содержат сезонный цикл, а тренд временного ряда может быть описан линейным трендом.

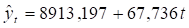
Объем реализации продукции фирмы АО "Лен" за последние три года приведен в таблице 3.5

Таблица 3.5 - Объем реализации продукции фирмы АО "Лен" за последние три года

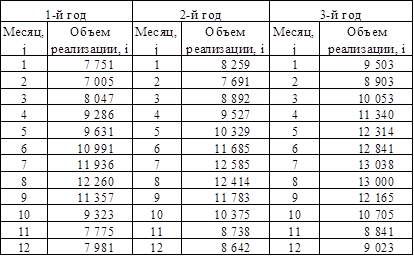
Определим объем реализации продукции на основе линейного тренда:

В декабре 1-го года

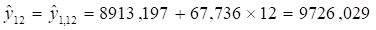
В декабре 2-го года

В декабре 3-го года

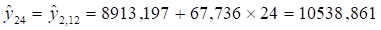
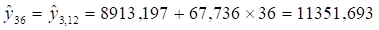
Найдем отклонение фактических данных от тренда:

В декабре 1-го года

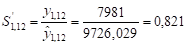
В декабре 2-го года

В декабре 3-го года

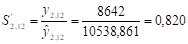
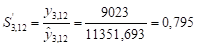
На основе отклонений фактических данных от тренда определим сезонные индексы для момента времени, т. е. сезонный индекс для декабря:

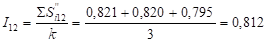
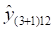
Перед определением сезонного прогноза найдем значение тренда в декабре 4-го года. Исходный ряд содержит данные за три года (k = 3), период упреждения прогноза, согласно условию задачи, равен одному году (ф = 1), декабрь имеет номер 12, поэтому декабрь 4-го года будет иметь номер или. Отсюда объем реализации продукции в декабре 4-го года по тренду

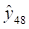
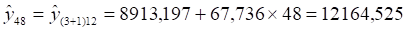
В итоге точечный прогноз объема реализации продукции в декабре 4-го года

Прогнозный объем реализации продукции фирмы АО "Лен" на декабрь 2008 г. составит 9 877,594 руб.

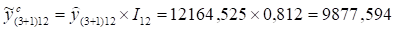
Приложения

Приложение 1

Значения средней м и стандартных ошибок У1, У2 для N= 10... 50

N	М	У1	У2
10 15 20 25 30	3,858 4,636 5, 195 5,632 5,990	1,288 1,521 1,677 1,791 1,882	1,964 2,153 2,279 2,373 2,447

Приложение 2

Значение T-критерия Стьюдента

Число

Степеней свободы

Доверительная вероятность

Число

Степеней свободы

Доверительная вероятность

0,9

0,95

0,9

0,95

1 2 3 4 5 6 7 8 9 10

6,314 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 1,812

12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228

11 12 13 14 15 16 17 18 19 20

1,796 1,782 1,771 1,761 1,753 1,746 1,740 1,734 1,729 1,725

2, 201 2,179 2,160 2,145 2,131 2,120 2,110 2,103 2,093 2,086

Примечание. В полном объеме значения T-критерия Стьюдента можно найти в любом учебнике по математической статистике (например, Калинина В. Н., Панкин В. Ф. Математическая статистика: Учеб. для техникумов. - М.: Высш. шк., 1998.).

Приложение 3

Значения RS-критерия для N = 10 ... 30

Число уровней ряда N	Нижняя граница интервала RSNH	Верхняя граница интервала RSNB
10 20 30	2,67 3,18 3,47	3,85 4,49 4,89

Приложение 4

Распределение критерия Дарбина-Уотсона для положительной автокорреляции (для 5% - го уровня значимости)

Число уровней

Ряда N

Число факторов

V=1

Число факторов

V=2

Нижняя граница

Интервала D1

Верхняя граница

Интервала D2

Нижняя граница

Интервала D1

Верхняя граница

Интервала D2

11 12 13 14 15 16 17 18 19 20

0,61 0,7 0,76 0,82 0,88 0,93 0,97 1,01 1,05 1,08 1,10 1,13 1,16 1,18 1, 20

1,4 1,36 1,33 1,32 1,32 1,32 1,33 1,34 1.35 1,36 1,37 1,38 1,39 1,40 1,41

0,95 0,98 1,02 1,05 1,08 1,10

1,54 1,54 1,54 1,53 1,53 1,54

Приложение 5

Значения коэффициента автокорреляции RAT

Число уровней

Ряда N

Положительное значение

Коэффициента автокорреляции RAT

Отрицательное значение

Коэффициента автокорреляции RAT

А=0,05

А=0,01

А=0,05

А=0,01

5 6 7 8 9 10 11 12 13 14 15 20

0,253 0,345 0,370 0,371 0,366 0,360 0,353 0,348 0,341 0,335 0,328 0,299

0,297 0,447 0,510 0,531 0,533 0,525 0,515 0,505 0,495 0,485 0,475 0,432

-0,753 0,708 0,674 0,625 0,593 0,564 0,539 0,516 0,497 0,479 0,462 0,399

-0,798 0,863 0,799 0,764 0,737 0,705 0,679 0,655 0,634 0,615 0,597 0,524

Приложение 6

Значение К для оценки доверительных интервалов прогноза при вероятности Г=0,9 (линейный тренд)

Число уровней

Ряда N

Период упреждения прогноза Ф

11 12 13 14 15 16 17 18 19 20

2,638

2,4631 2,3422 2,2524 2,1827 2,1274 2,0837 2,0462 2,0153 1,9883 1,9654 1,9455 1,928 1,9117

2,8748 2,6391 2,4786 2,3614 2,2718 2, 2017 2,1463 2,1000 2,0621 2,0292 2,0015 1,9776 1,9568 1,9375

3,1399 2,8361 2,631 2,4827 2,3706 2,2836 2,2155 2,1590 2,1131 2,0735 2,0406 2,0124 1,9877 1,9654

Приложение 7

Значение К? для оценки доверительных интервалов прогноза при вероятности Г=0,9 (параболический тренд)

Число уровней

Ряда N

Период упреждения прогноза Ф

11 12 13 14 15 16 17 18 19 20

3,948

3,459 3,144 2,926 2,763 2,636 2,536 2,455 2,386 2,330 2,280 2,238 2, 201 2,169

5,755 4,754 4,124 3,695 3,384 3,148 2,965 2,820 2,701 2,604 2,521 2,451 2,391 2,339

8,152 6,461 5,408 4,698 4,189 3,808 3,516 3,286 3,100 2,950 2,823 2,717 2,627 2,549

Задание 2. "Прогнозирование на основе тренда временного ряда" - Методы прогнозирования в экономической статистике

Похожие статьи