Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин
Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится.
Не будет лишним помнить, что этот закон (или просто - распределение случайной величины) можно задать тремя способами:
в виде формулы: например, для биномиального распределения при n=3 и p=0.5 вероятность значения суммы S=2 составляет 0.375;
в виде таблицы значений величины и соответствующих им вероятностей:
в виде диаграммы или, как ее иногда называют, Гистограммы распределения:
Таблица 2-1
|
Сумма |
0 |
1 |
2 |
3 |
|
Вероятность |
0.125 |
0.375 |
0.375 |
0.125 |
Рис. 2-1 Гистограмма распределения
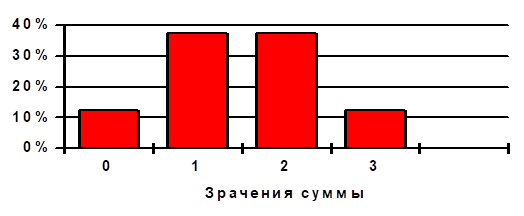
Необходимость рассматривать вопрос, поставленный в заглавии параграфа, не так уж и очевидна, поскольку непонятно, что же еще нам надо знать?
Между тем, все достаточно просто. Пусть, для какого-то реального явления или процесса мы сделали допущение (выдвинули гипотезу), что соответствующая СВ принимает свои значения в соответствии с некоторой схемой событий. Рассчитать вероятности по принятой нами схеме -- не проблема!
Вопрос заключается в другом - как проверить свое допущение или, на языке статистики, оценить достоверность гипотезы?
По сути дела, кроме обычного наблюдения за этой СВ у нас нет иного способа выполнить такую проверку. И потом - в силу самой природы СВ мы не можем надеяться, что через достаточно небольшое число наблюдений их частоты превратятся в "теоретические" значения, в вероятности. Короче - результат наблюдения над случайной величиной тоже ... случайная величина или, точнее, - множество случайных величин.
Так или примерно так рассуждали первые статистики-профессионалы. И у кого-то из них возникла простая идея: сжать информацию о результатах наблюдений до одного, единственного показателя!
Как правило, простые идеи оказываются предельно эффективными, поэтому способ оценки итогов наблюдений по одному, желательно "главному", "центральному" показателю пережил все века становления прикладной статистики и по ходу дела обрастал как теоретическими обоснованиями, так и практическими приемами использования.
Вернемся к гистограмме рис. 2-1 и обратим внимание на два, бросающихся в глаза факта:
"наиболее вероятными" являются значения суммы S=1 и S=2 и эти же значения лежат "посредине" картинки;
вероятность того, что сумма окажется равной 0 или 1, точно такая же, как и вероятность 2 или 3, причем это значение вероятности составляет точно 50 %.
Напрашивается простой вопрос - если СВ может принимать значения 0, 1, 2 или 3, то сколько в среднем составляет ее значение или, иначе - что мы ожидаем, наблюдая за этой величиной?
Ответ на такой вопрос на языке математической статистики состоит в следующем. Если нам известен закон распределения, то, просуммировав произведения значений суммы S на соответствующие каждому значению вероятности, мы найдем Математическое ожидание этой суммы как дискретной случайной величины -
M(S) = S I P(S I). {2-3}
В рассматриваемом нами ранее примере биномиального распределения, при значении p=0.5, математическое ожидание составит
M(S) = 00.125+10.375+20.375+30.125= 1.5 .
Обратим внимание на то, что математическое ожидание дискретной величины типа Int или Rel совсем не обязательно принадлежит к множеству допустимых ее значений. Что касается СВ типа Nom или Ord, то для них понятие математического ожидания (по закону распределения), конечно же, не имеет смысла. Но так как с номинальной, так и с порядковой шкалой дискретных СВ приходится иметь дело довольно часто, то в этих случаях прикладная статистика предлагает особые, Непараметрические методы.
Продолжим исследование свойств математического ожидания и попробуем в условиях нашего примера вместо S рассматривать U= S - M(S). Такая замена СВ (ее часто называют центрированием) вполне корректна: по величине U всегда можно однозначно определить S и наоборот.
Если теперь попробовать найти математическое ожидание новой (не обязательно дискретной) величины M(U) , то оно окажется равным нулю, независимо от того считаем ли мы конкретный пример или рассматриваем такую замену в общем виде.
Мы обнаружили самое важное свойство математического ожидания - оно является "центром" распределения. Правда, речь идет вовсе не о делении оси допустимых значений самой СВ на две равные части. Поистине - первый показатель закона распределения "самый главный" или, на языке статистики, - центральный.
Итак, для СВ с числовым описанием математическое ожидание имеет достаточно простой смысл и легко вычисляется по законам распределения. Заметим также, что математическое ожидание - просто числовая величина (в общем случае не дискретная, а непрерывная) и никак нельзя считать ее случайной.
Другое дело, что эта величина зависит от внутренних параметров распределения (например, - значения вероятности р числа испытаний n биномиальном законе).
Так для приведенных выше примеров дискретных распределений математическое ожидание составляет:
|
Тип распределения |
Математическое ожидание |
|
Биномиальное |
Np |
|
Распределение Паскаля |
K q / p |
|
Геометрическое распределение |
Q / p |
|
Распределение Пуассона |
Возникает вопрос - так что же еще надо? Ответ на этот вопрос можно получить как из теории, так и из практики.
Один из разделов кибернетики - теория информации (курс "Основы теории информационных систем" у нас впереди) в качестве основного положения утверждает, что всякая свертка информации приводит к ее потере. Уже это обстоятельство не позволяет допустить использование только одного показателя распределения СВ - ее математического ожидания.
Практика подтверждает это. Пусть мы построили (или использовали готовые) законы распределения двух случайных величин X и Y и получили следующие результаты:
Таблица 2-2
|
Значения |
1 |
2 |
3 |
4 |
|
P(X) % |
12 |
38 |
38 |
12 |
|
P(Y) % |
30 |
20 |
20 |
30 |
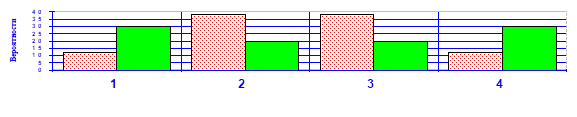
Рис. 2-2
Простое рассмотрение табл.2-2 или соответствующих гистограмм рис.2-2 приводит к выводу о равенстве M(X) = M(Y) = 0.5 , но вместе с тем столь же очевидно, что величина X является заметно "менее случайной", чем Y.
Приходится признать, что математическое ожидание является удобным, легко вычислимым, но весьма неполным способом описания закона распределения. И поэтому требуется еще как-то использовать полную информацию о случайной величине, свернуть эту информацию каким-то иным способом.
Обратим внимание, что большие отклонения от M(X) у величины X маловероятны, а у величины Y - наоборот. Но при вычислении математического ожидания мы, по сути дела "усредняем" именно отклонения от среднего, с учетом их знаков. Стоит только "погасить" компенсацию отклонений разных знаков и сразу же первая СВ действительно будет иметь показатель разброса данных меньше, чем у второй. Именно такую компенсацию мы получим, усредняя не сами отклонения от среднего, а квадраты этих отклонений.
Соответствующую величину
D(X) = (X I - M(X))2 P(X I); {2-4} принято называть Дисперсией распределения дискретной СВ.
Ясно, что для величин, имеющих единицу измерения, размерность математического ожидания и дисперсии оказываются разными. Поэтому намного удобнее оценивать отклонения СВ от центра распределения не дисперсией, а квадратным корнем из нее - так называемым среднеквадратичным отклонением, т. е. полагать
2 = D(X). {2-5}
Теперь оба параметра распределения (его центр и мера разброса) имеют одну размерность, что весьма удобно для анализа.
Отметим также, что формулу {2-3} часто заменяют более удобной
D(X) = (X I)2 P(X I) - M(X)2. {2-6}
Весьма полезно будет рассмотреть вопрос о предельных значениях дисперсии.
Подобный вопрос был бы неуместен по отношению к математическому ожиданию -- мало ли какие значения может иметь дискретная СВ, да еще и со шкалой Int или Rel.
Но дословный перевод с латыни слова "дисперсия" означает "рассеяние", "разброс" и поэтому можно попытаться выяснить - чему равна дисперсия наиболее или наименее "разбросанной" СВ? Скорее всего, наибольший разброс значений (относительно среднего) будет иметь дискретная случайная величина X, у которой все n допустимых значений имеют одну и ту же вероятность 1/n. Примем для удобства XMin И XMax (пределы изменения данной величины), равными 1 и n соответственно.
Математическое ожидание такой, Равномерно распределенной случайной величины составит M(X) = (n+1)/2 и остается вычислить дисперсию, которая оказывается равной D(X) = (XI)2/n - (n+1)2/4 = (n2-1)/ 12.
Можно доказать, что это наибольшее значение дисперсии для дискретной СВ со шкалой Int или Rel.
Последнее выражение позволяет легко убедиться, что при n =1 дисперсия оказывается Равной нулю - ничего удивительного: в этом случае мы имеем дело с детерминированной, неслучайной величиной.
Дисперсия, как и среднеквадратичное отклонение для конкретного закона распределения являются просто числами, в полном смысле показателями этого закона.
Полезно познакомиться с соотношениями математических ожиданий и дисперсий для упомянутых ранее стандартных распределений:
Таблица 2-3
|
Тип Распределения |
Математическое ожидание |
Дисперсия |
Коэффициент Вариации |
|
Биномиальное |
Np |
Npq |
Sqrt(q/np) |
|
Паскаля |
kq/p |
Kq/p2 |
Sqrt(1/ kq) |
|
Геометрическое |
q/p |
Q/p2 |
Sqrt(1/q) |
|
Пуассона |
Sqrt(1/) |
Можно ли предложить еще один или несколько показателей - сжатых описаний распределения дискретной СВ? Разумеется, можно.
Первый показатель (математическое ожидание) и второй (дисперсия) чаще всего называют Моментами распределения. Это связано со способами вычисления этих параметров по известному закону распределения - через усреднение значений самой СВ или усреднение квадратов ее значений.
Конечно, можно усреднять и кубы значений, и их четвертые степени и т. д., но что мы при этом получим? Поищем в теории ответ и на эти вопросы.
Начальными моментами k-го порядка случайной величины X обычно называют суммы:
K = (X I)K P(X I); 0 = 0; {2-7}
А Центральными моментами - суммы:
K= (X I -1)K P(X I), {2-8} при вычислении которых усредняются отклонения от центра распределения - математического ожидания.
Таким образом,
1 = 0;
1 = M(X) является параметром Центра распределения;
2 = D(X) является параметром Рассеяния; {2-9}
3 И 3 - описывают Асимметрию распределения;.
4 И 4 - описывают т. н. Эксцесс (выброс) распределения и т. д.
Иногда используют еще один показатель степени разброса СВ - коэффициент вариации V= / M(X), имеющий смысл при ненулевом значении математического ожидания.
Похожие статьи
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
применяем 2е теоремы: -формула полной вероятности Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H1, H2, ..., Hn...
-
Вопросы по теории вероятностей - Случайные величины
Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. Сумма и произведение событий, теоремы сложения и...
-
Односторонние и двухсторонние значения вероятностей - Распределение вероятности случайных величин
Если нам известен закон распределения СВ (пусть - дискретной), то в этом случае очень часто приходится решать задачи, по крайней мере, трех стандартных...
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Обозначим вероятность соответствующих событий через Pi - Случайные величины
, Так как рассматриваемые события образуют полную группу не совместных событий, то Х полностью описана с вероятностной точки зрения, если мы зададим...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
Нормальное распределение - Распределение вероятности случайных величин
Первым, фундаментальным по значимости, является т. н. Нормальный закон Распределения непрерывной случайной величины X, для которой допустимым является...
-
Законы распределений дискретных случайных величин. - Распределение вероятности случайных величин
Пусть некоторая СВ является дискретной, т. е. может принимать лишь фиксированные (на некоторой шкале) значения X I. В этом случае ряд значений...
-
Непрерывные величины - возможные значение, которых непрерывно заполняют некоторый диапазон. Плотность распределения вероятности непрерывной случайной...
-
В общем случае: , где Для не корреляционных случайных величин: Ответ на билет 15 В широком смысле слова, закон больших чисел характеризует устойчивость...
-
Большую роль в теории и практике системного анализа играют некоторые стандартные распределения непрерывных и дискретных СВ. Эти распределения иногда...
-
Распределения непрерывных случайных величин - Распределение вероятности случайных величин
До этого момента мы ограничивались только одной "разновидностью" СВ - дискретными, т. е. принимающими конечные, заранее оговоренные значения на любой из...
-
Шкалирование случайных величин - Распределение вероятности случайных величин
Как уже отмечалось, дискретной называют величину, которая может принимать одно из счетного множества так называемых "допустимых" значений. Примеров...
-
Статистическая вероятность и распределения случайных величин - Основы научных исследований
В теории вероятностей под случайной величиной понимают отношения числа благоприятных исходов испытаний к общему числу испытаний. Например, если из 10...
-
Пусть у нас имеется некоторая непрерывная случайная величина X, распределенная нормально с математическим ожиданием и среднеквадратичным отклонением....
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Математическое ожидание генеральной совокупности назовем генеральной средней, т. е. . Теорема. Выборочное среднее есть состоятельная и несмещенная оценка...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Контрольная работа По дисциплине: Теория вероятностей Контрольная работа № 1 Вариант 1 Задача № 1 Условие: Из 10 изделий, среди которых 4 бракованные,...
-
Выборочные распределения на шкалах Int и Rel
Оценка наблюдений при неизвестном законе распределения Какова цель наблюдений над случайной величиной; для чего используются результаты наблюдений; где,...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Взаимосвязи случайных событий - Закон распределения случайной величины
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти)....
-
Генеральная и выборочная совокупности Для обнаружения закономерностей, описывающих исследуемое массовое явление, необходимо иметь опытные данные,...
-
Введение - Математическое ожидание случайной величины
Математическая статистика - наука, изучающая методы исследования закономерностей в массовых случайных явлениях и процессах по данным, полученным из...
-
Вариационные ряды - Математическое ожидание случайной величины
После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине - т. е....
-
Случайные события и случайные величины - Основы научных исследований
Вероятностные закономерности проявляются только в массовых явлениях, т. е. когда один и тот же объект изменяет свое состояние многократно или когда...
-
Параметры эмпирических распределений - Основы научных исследований
По опытным (эмпирическим) данным строятся распределения исследуемых случайных величин. Функции плотности Р(х) таких распределений могут иметь один...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Выборочные распределения, Распределение Стьюдента - Основы научных исследований
Выборочное распределение - это распределение какой-либо статистики, полученное в результате отбора различных случайных выборок из одной и той же...
-
Распределение Вейбулла, Нормальное распределение - Законы надежности
Двухпараметрическое распределение Вейбулла является более гибким, чем экспоненциальное, которое может рассматриваться как частный случай первого....
-
ТВ-раздел математики, в которой используются различные разделы математики для своего развития. Задача: выяснение закономерностей, возникающих при...
-
Экспоненциальное распределение - Законы надежности
Известное выражение для вероятности безотказной работы при = const превращается в зависимость, соответствующую экспоненциальному закону распределения ,...
-
Нормальное распределение - Основы научных исследований
В классической математической статистике чаще всего используется т. н. нормальное распределение или распределение Гаусса-Лапласа. В естествознании и...
-
Проверка гипотез о законе распределения, Критерий К. Пирсона - Проверка статистических гипотез
Критерий К. Пирсона Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим...
-
Дисперсия - Основы научных исследований
Степень рассеивания случайной величины относительно центра распределения характеризуется Дисперсией (от лат. dispersio - рассеивание). Дисперсия - это...
-
Литература - Математическое ожидание случайной величины
1. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977. 2. Гмурман В. Е. Руководство к решению задач по теории...
-
В решении любой прикладной задачи можно выделить три основных этапа: - Построение математической модели исследуемого объекта - Выбор способа и алгоритма...
-
Распределением признака Называется закономерность встречаемости разных его значений. Нормальное распределение Характеризуется тем, что крайние значения...
Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин