Свойства дисперсии, Что называется полигоном, гистограммой, кумулятой? Как их строить? - Математическая статистика
- 1. Если значения измеренного признака не отличаются друг от друга (равны между собой) - дисперсия равна нулю. Это соответствует отсутствию изменчивости в данных. 2. Прибавление одного и того же числа к каждому значению переменной не меняет дисперсию.
Dx+c = Dx так как У [(xj + с) - (Mx + c)]І = У (xj - Mx)І.
Прибавление константы к каждому значению переменной сдвигает график распределения этой переменной на эту константу (меняется среднее), но изменчивость (дисперсия) при этом остается неизменной.
3. Умножение каждого значения переменной на константу с изменяет дисперсию в сІ раз:
Dx-c = Dx-сІ так как У [(xj - с) - (Mx - c)]І = сІУ (xj - Mx)І.
При объединении двух выборок с одинаковой дисперсией, но с разными средними значениями дисперсия увеличивается.
Что называется полигоном, гистограммой, кумулятой? Как их строить?
Для наглядности принято использовать следующие формы графического представления статистических распределений:
Дискретный ряд изображают в виде полигона. Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (I , I); аналогично, Полигон относительных частот - ломаная, отрезки которой соединяют точки с координатами (, WI );
Пример 1. Имеется распределение 80 предприятий по числу работающих на них (чел.):
|
150 |
250 |
350 |
450 |
550 |
650 |
750 |
|
1 |
3 |
7 |
30 |
19 |
15 |
5 . |
Решение. Признак Х - число работающих (чел.) на предприятии. В данной задаче признак Х является дискретным. Поскольку различных значений признака сравнительно немного - K = 7, применять интервальный ряд для представления статистического распределения нецелесообразно (в прикладной статистике в подобных задачах часто используют именно интервальный ряд). Ряд распределения - дискретный. Построим полигон распределения частот (рис. 1).
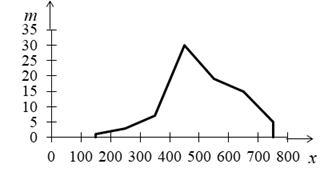
Рис. 1
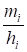
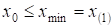
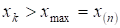
Интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых - интервалы длиной, а высоты - плотности частот. В случае Гистограммы относительных частот высоты прямоугольников - плотности относительных частот. Здесь в общем случае, однако на практике чаще всего полагают величину H одинаковой для всех интервалов: . Очевидно для ранжированного вариационного ряда ; . В скобках указаны индексы J Исходного ранжированного вариационного ряда.
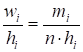
Площадь гистограммы есть сумма площадей ее прямоугольников:
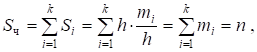
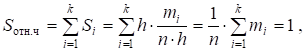
Таким образом, площадь гистограммы частот равна объему выборки, а площадь гистограммы относительных частот равна единице.
В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятностей. Поэтому гистограмму можно использовать для подбора закона распределения генеральной совокупности;
Пример 2. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин):
|
XI-1-XI |
22-24 |
24-26 |
26-28 |
28-30 |
30-32 |
32-34 |
|
2 |
12 |
34 |
40 |
10 |
2 . |
Решение. Признак Х - затраты времени на обработку одной детали (мин). Признак Х - непрерывный, ряд распределения - интервальный. Построим гистограмму частот (рис. 2), предварительно определив (K = 6) и плотность частоты :
|
XI-1-XI |
22-24 |
24-26 |
26-28 |
28-30 |
30-32 |
32-34 |
|
1 |
6 |
17 |
20 |
5 |
1 . |
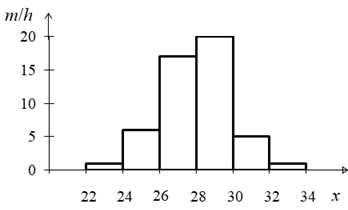
Рис. 2
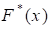
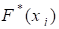
Кумулятивные ряды графически изображают в виде Кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат - накопленные частоты Н() или относительные накопленные частоты, а затем точки с координатами (I ; H(I )) или (I ; ) соединяют отрезками прямой. В теории вероятностей кумуляте соответствует график интегральной функции распределения.
Пример 3. В распределении, данном в примере 1, найти накопленные частоты H(i ) и построить кумуляту.
Решение. Используем: H(X1) = 0, H(XI) = H(XI-1) + MI-1 (I=2,3,, K+1 , k = 7).
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
XI |
150 |
250 |
350 |
450 |
550 |
650 |
750 |
850 |
|
MI |
1 |
3 |
7 |
30 |
19 |
15 |
5 |
0 |
|
H(I ) |
0 |
0+1=1 |
1+3=4 |
4+7=11 |
11+30=41 |
41+19=60 |
60+15=75 |
75+5=80. |
На рис. 3 показана кумулята распределения предприятий по числу работающих (чел.).
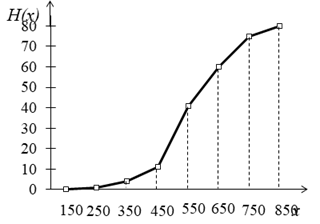
Рис. 3
Пример 4. В распределении, данном в примере 2, составить эмпирическую функцию распределения и построить кумуляту относительных частот.
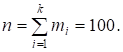
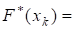
Решение. Используем: H(X0) = 0, H(XI) = H(XI-1) + MI (I=1,2,, K , k = 6). ; Проверка: 1.
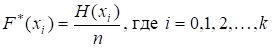
I |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
XI-1-XI |
--22 |
22-24 |
24-26 |
26-28 |
28-30 |
30-32 |
32-34 |
|
MI |
0 |
2 |
12 |
34 |
40 |
10 |
2 |
|
H(I ) |
0 |
0+2=2 |
2+12=14 |
14+34=48 |
48+40=88 |
88+10=98 |
98+2=100 |
|
0 |
0,02 |
0,14 |
0,48 |
0,88 |
0,98 |
1. |
Построим кумуляту распределения (см. рис. 4).

Рис. 4
Похожие статьи
-
Распределением признака Называется закономерность встречаемости разных его значений. Нормальное распределение Характеризуется тем, что крайние значения...
-
Мы можем определить вариацию как среднее значение отклонений каждого из вариантов от средней арифметической, согласно свойству средней арифметической,...
-
Среднее арифметическое - Числовая характеристика совокупности чисел а1, .... аn, определяемая формулой: В = (а1 + .....+аn) / n Среднее гармоническое -...
-
Признак, частота признака, кумулятивная частота - Математическая статистика
Основной величиной в статистических измерениях является единица статистической совокупности. Единица статистической совокупности характеризуется набором...
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Квантиль - Это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением...
-
Признаки Х и Y находятся в Корреляционной зависимости , если каждому значению одного признака X I соответствует определенная Условная средняя другого...
-
Математическое ожидание генеральной совокупности назовем генеральной средней, т. е. . Теорема. Выборочное среднее есть состоятельная и несмещенная оценка...
-
Выборочное среднее и выборочная дисперсия - Математическое ожидание случайной величины
Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Основные характеристики выборки и генеральной совокупности - Математическая статистика
Числовые характеристики генеральной совокупности называются Генеральными параметрами или просто Параметрами . Например, параметрами нормального...
-
Определение выборки и генеральной совокупности - Математическая статистика
Генеральная совокупность - идеализация реальной совокупности (теоретически бесконечная), из которой производится выборка конечного объема для...
-
Статистики, Свойства оценок - Основы научных исследований
Любая функция от элементов выборки называется Статистикой . Следовательно, точечная оценка также является статистикой. Однако не всякая статистика может...
-
В 2011 - 2015 гг. в серии статей в научных журналах и докладов на международных, зарубежных и всероссийских научных конференциях была представлена...
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью...
-
Моделирование тарифов Водоканала и РАО ЕЭС, Тарифы водоканала - Статистика ЖКХ
Тарифы водоканала Изучим динамику цен на услуги водоканала. Данные возьмем с сайта организации http://www. vodokanal. spb. ru. Показатель: условия...
-
Определение типов измерения измерительных шкал
Цель контрольной работы -- самостоятельная практическая проверка усвоения учебного материала по разделу "Описательная статистика". Задачи контрольной...
-
Понятие "показатель асимметрии", Понятие "показатель эксцесса" - Математическая статистика
Когда график вариационного ряда (распределение набора данных) скошен в правую сторону больше, чем в левую, то мы говорим, что распределение имеет...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Для регрессии вида Найдем коэффициенты по формулам Вычислим Тогда Откуда Тогда линейная регрессия будет иметь вид Смысл коэффициента beta заключается в...
-
Средняя арифметическая Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в...
-
Методы прогнозирования в статистике населения - Система источников данных о населении
Моделирование временного тренда среднегодовой численности занят Ого населения Санкт-Петербурга Приведем данные среднегодовой численности занятого...
-
Односторонние пределы, Пределы на бесконечности - Свойства функций
В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Реализуем математическую модель (2) (6) в MS Excel. Для этой цели построим таблицы исходных данных задачи по расчету оптимального графика занятости при...
-
Метод конечных разностей -- широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на...
-
Критерий Дарбина-Уотсона для выявления автокорреляции - Ряды динамики в статистике
Ряд динамика аналитический прогнозирование автокорреляция Критерий Дарбина-Уотсона предназначен для обнаружения автокорреляции первого порядка. Он...
-
Методы классификации - неотъемлемая часть математических методов исследования, интересная теоретически и важная практически. Обзоры этой научной области...
-
Методы измерения параметров тренда - Ряды динамики в статистике
Тенденция ряда динамики (тренд). Важнейшим направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей...
-
Критерий Мизеса, Статистика критерия - Проверка статистических гипотез
В качестве меры различия теоретической функции распределения F(x) и эмпирической Fn(x) по критерию Мизеса (критерию w 2) выступает средний квадрат...
-
Вариационные ряды - Математическое ожидание случайной величины
После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине - т. е....
-
Дисперсия - Основы научных исследований
Степень рассеивания случайной величины относительно центра распределения характеризуется Дисперсией (от лат. dispersio - рассеивание). Дисперсия - это...
-
Степенное среднее - Степенные величины в статистике
Для наглядности наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в...
-
Изучив основные вопросы, связанные с календарным планированием, подведем итог. Задачи календарного планирования отражают процесс распределения во времени...
-
Распределение Фишера, Статистические гипотезы - Основы научных исследований
Служит для сравнения дисперсий разных статистических совокупностей разных случайных величин Х 1 и Х 2 . Ему подчиняется статистика (10.5) Где S2(x 1 ) >...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
Тема: Статистическое изучение объема, состава и динамики доходов и расходов государственного бюджета Имеются следующие выборочные данные (выборка 25%-ная...
-
ДОПУЩЕНИЯ МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА, ФАКТОРНЫЙ АНАЛИЗ - Многомерный статистический анализ
Регрессионная модель при оценке параметров и проверке значимости исходит из ряда допущений: 1. Ошибочный член уравнения регрессии (остаточный компонент)...
-
ПРИНЦИПЫ ИЗМЕРЕНИЙ И ШКАЛИРОВАНИЯ - Многомерный статистический анализ
Измерение шкалирование кластерный регрессионный Измерение - это Присвоение чисел или других символов характеристикам объектов по заранее определенным...
Свойства дисперсии, Что называется полигоном, гистограммой, кумулятой? Как их строить? - Математическая статистика