В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: max&;nbsp;f(X)&;nbsp;= min&;nbsp;g(Y). - Теория игр
Значит и

Вторая теорема двойственности (теорема о дополняющей нежесткости)
Пусть - допустимое решение прямой задачи, а - допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

Эти условия позволяют, зная оптимальное решение одной из взаимодвойственных задач, найти оптимальное решение другой задачи, используя такие требования на оптимальное решение и оптимальный вектор оценок :
Если
Если
Если
Если





Проверим, какие из ограничений задачи второго игрока превращаются в равенства, а какие в неравенства:

Значит

Подставляем в систему ограничений задачи первого игрока

Полученное оптимальное решение имеет вид:
Перейдем к исходным переменным:
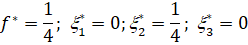

Из полученных результатов следует, что максимальный гарантированный выигрыш первого игрока составит 4 при условии, что он будет применять только свою вторую стратегию.
В данной задаче такое решение было очевидно еще при анализе матрицы
Имеется точка равновесия (2;1).
Рассматривается корпоративная игра с тремя игроками. Известны значения характеристической функции, определяющие соответственно выигрыши первого, второго и третьего игроков, когда каждый из них играет в одиночку, не кооперируясь ни с кем из других игроков: V(1)=1500; V(2)=1200; V(3)=1000; а также выигрыши, которые они могут обеспечить себе, действуя попарно: V(1,2)=3000; V(1,3)=2700; V(2,3)=2400; и общий выигрыш, который могут обеспечить себе игроки, образуя максимально большую коалицию, состоящую из трех игроков V(1,2,3)=4400. Требуется:
Проверить выполнение условий супераддитивности и существенности для данной кооперативной игры;
Выразить значение характеристической функции в 0-1 редуцированной форме;
Проверить условия, определяющие непустоту С-ядра и найти один из вариантов решения игры (дележ Х);
Определить выигрыши каждого из игроков в случае их объединения на основе использования вектора Шепли. Проверить принадлежность вектора Шепли С-ядру.
Решение.
Пусть N = {1,..., n} -- множество всех игроков. Любое непустое подмножество S N называется коалицией.
Свойство супераддитивности. (Определение) Характеристической функцией игры n лиц будем называть вещественную функцию х, определенную на коалициях S N, при этом для любых непересекающихся коалиций Т, S (Т С N, S С N) выполняется неравенство
V{T) +v{S) < u(TS), v()=0
В данной задаче
V(1)=1500; V(2)=1200; V(3)=1000; V(1,2)=3000; V(1,3)=2700; V(2,3)=2400; V(1,2,3)=4400.



Также



Значит свойство супераддитивности выполняется.
Теорема. Каждая существенная кооперативная игра эквивалентна некоторой игре в (0-1) -- редуцированной форме.
Если н -- характеристическая функция произвольной существенной игры (Н, н), то

Есть (0 - 1) - нормализация, соответствующая функции н.







Получили такую редуцированную функцию

Проверим условия, определяющие непустоту С-ядра и найдем один из вариантов решения игры (дележ ).
Определение. Множество недоминируемых дележей кооперативной игры (N, н)называется ее С-ядром.
Теорема. Для того чтобы дележ а принадлежал С-ядру, необходимо и достаточно выполнение для всех S N неравенств

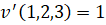

С-ядро не пусто тогда и только тогда, когда для всех |S| = 1,..., n имеет место неравенство

Таким образом, С-ядро непусто тогда и только тогда, когда не существует промежуточной коалиции S, в которой средняя доля каждого игрока больше соответствующей величины в коалиции Н.
В нашей задаче средняя доля каждого игрока в коалиции Н равна




Условия непустоты С-ядра выполняются.
Чтобы дележ а принадлежал С-ядру, необходимо и достаточно выполнение следующих неравенств:


Например a=(3/7; 3/7; 1/7) или a=(6/14; 5/14; 3/14)
Определим выигрыши каждого из игроков в случае их объединения на основе использования вектора Шепли. Проверим принадлежность вектора Шепли С-ядру.
В соответствие каждой кооперативной игре (Н, х)можно поставить вектор ц(н) = (ц1[х],..., цз[н]), компоненты которого будем интерпретировать как выигрыши, полученные игроками в результате соглашения или решения арбитра. При этом будем считать, что указанное соответствие удовлетворяет следующим аксиомам.
Аксиомы Шепли.
1. Если S -- любой носитель игры (Н, н), то

- 2. Для любой подстановки р и i N 3. Если (N, u) и (Н, v) -- две любые кооперативные игры, то


Определение. Пусть ц -- функция, ставящая в соответствие согласно аксиомам 1--3 каждой игре (N, н) вектор ц[н]. Тогда ц[v] называется вектором значений или вектором Шепли игры (Н, н).
Для 0-1 редуцированной формы игры с тремя игроками вектор Шепли рассчитывается следующим образом:
Ф1(v) = 1/6 (2 - 2C1 + C2 + C3)
Ф2(v) = 1/6 (2 - 2C2 + C1 + C3)
Ф3(v) = 1/6 (2 - 2C3 + C1 + C2)
Где где C1 = v(2,3); C2 = v(1,3); C3 = v(1,2).
Соответственно

Проверим принадлежность вектора Шепли С-ядру.
Чтобы дележ ф принадлежал С-ядру, необходимо и достаточно выполнение следующих неравенств:







Все условия выполняются, значит дележ ф принадлежит ядру.
В нередуцированной форме

Получили
Чтобы дележ ф принадлежал С-ядру, необходимо и достаточно выполнение следующих неравенств:
Все условия выполняются, значит дележ ф принадлежит ядру.
V(1)=1500; V(2)=1200; V(3)=1000; V(1,2)=3000; V(1,3)=2700; V(2,3)=2400; V(1,2,3)=4400.
Похожие статьи
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Рассмотрим конечные матричные игры, в которых нет седловой точки, т. е. . Нетрудно доказать, что. Если игра одноходовая, то по принципу минимакса игроку...
-
Пусть у игроков А и В соответственно M и N чистых стратегий, которые обозначим через и. Выбор игроками любой пары стратегий и однозначно определяет исход...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
В условиях рыночной экономики возникают ситуации, в которых сталкиваются интересы двух и более сторон. Такие ситуации относятся к конфликтным. Например,...
-
Найти все максиминные и минимаксные стратегии игроков, нижнюю и верхнюю цены игры. Указать все ситуации равновесия и решение игры. Принцип построения...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
Исследуем на экстремум функцию: 1. С помощью необходимого существования экстремума, т. е. из системы Найдем координаты стационарных (критических) точек:...
-
Объем выпуска продукции Y зависит от количества вложенного труда x как функция . Цена продукции v, зарплата p. Другие издержки не учитываются. Найти...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
Теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных...
-
Теория игр - Математическое моделирование экономических процессов
Одна из задач теории оптимальных решений - принятие решения в условиях неопределенности. Для обоснования решений разработаны специальные математические...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Решение задачи оптимального управления - Стохастическая полумарковская модель
Воспользуемся теоремой о структуре стационарного показателя качества управления, сформулированной в предыдущем разделе. Отметим, что рассматриваемая в...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
При решении некоторых задач линейного программирования бывает необходимо получить целочисленное решение, которое находится методами целочисленного...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Основная задача линейного программирования: Найти неотрицательное решение системы ограничений обеспечивающее максимум (минимум) целевой функции. Чтобы...
-
Первая симплексная таблица - Методы оптимальных решений
Величины Свободные члены Х1 Х2 Х3 Х4 F 0 - 60 - 70 - 120 - 130 У1 16 1 4 1 1 У2 110 6 5 4 3 У3 100 4 6 10 13 Проверка на допустимость и оптимальность...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Управление научной деятельностью представляет собой сложный процесс. В литературе подобного типа задачи рассматриваются путем построения иерархий, дерева...
-
Введение, Графический метод решения задач линейного программирования - Методы оптимальных решений
Задача линейного программирования может быть решена графическим методом, достоинство которого в его простоте и наглядности, но существенным недостатком...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Оптимальное решение модели. - Методика решения задачи целочисленного программирования
Рис. 1 Шаг 1. Исходную задачу 1 заносим в дерево задач. В качестве исходного допустимого решения берем: x1=x2=x3=0. Соответствующее значение целевой...
В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают: max&;nbsp;f(X)&;nbsp;= min&;nbsp;g(Y). - Теория игр