Линейная функция - Конформное отображение
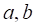
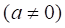
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной.
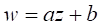
Определение 3. Отображение, осуществимое линейной функцией
Аналитической в комплексной плоскости, называют линейным.
Линейная функция обладает следующими свойствами.
1) Функция однолистна на.
Доказательство: Добавим к (3) условие
В бесконечно удаленной точке. Соотношения (3) и (4) опредеделяют однолистное отображение расширенной комплексной плоскости () на расширенную комплексную плоскость (). Проверяем однолистность:
и,
То
И, следовательно, равенство возможно только при.
2) Для линейной функции существует обратная функция:
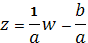
,
Которая также является линейной функцией
3) Во всех точках плоскости функция является дифференцируемой, причем ее производная вычисляется по формуле
.
Доказательство:
Для доказательства дифференцируемости функции найдем действительную и мнимую части линейной функции, покажем, что эти функции дифференцируемы, как функции 2-х действительных переменных, и выполняются условия К.-Р.
Т. к. , где и, то
+, или, что тоже самое,
Т. е.
Функции и являются многочленами первого порядка, а, следовательно, они дифференцируемы любое число раз как функции двух переменных.
Найдем их частные производные:
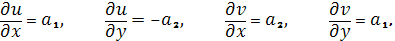
Отсюда следует, что
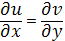
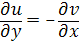
и.
Таким образом, условия К.-Р. выполняются. Следовательно, функция является дифференцируемой, и значит аналитической в. Кроме того,
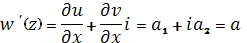
.
3) Линейная функция - голоморфна на всей плоскости (Функция называется голоморфной в, если в каждой точке области ее можно разложить в ряд Тейлора).
Доказательство:
Учитывая свойство 3) разложим линейную функцию в ряд Тейлора в любом
Т. е. таким образом, линейная функция является аналитической и однозначной, голоморфна в.
5) Для любой точки существует, поэтому отображение функцией - является конформным во всех точках плоскости.
Отображение с помощью линейной функции:
Рассмотрим сначала частные специальные случаи линейных функций:
1) Пусть, тогда В этом случае каждая конечная точка смещается в точку, т. е. происходит параллельный перенос всех точек комплексной плоскости на вектор, соответствующий комплексному числу.(рис. 2)
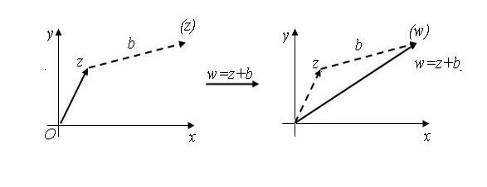
Рис. 2
2) Пусть, тогда Это отображение осуществляет преобразование поворота вокруг начала координат на угол (рис. 3), т. к. для имеем.
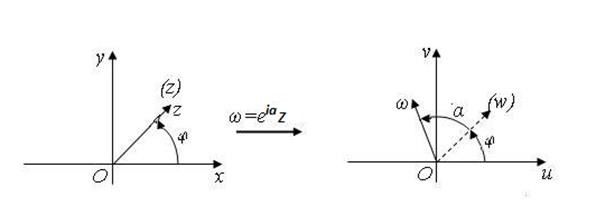
Рис. 3
3) Пусть и тогда В этом случае отображение оставляет неизменным аргумент комплексного числа, но его модуль изменяется в раз (рис. 4). Такое отображение представляет собой преобразование подобия с центром подобия в точке и коэффициентом подобия.
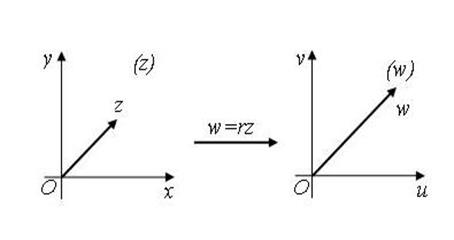
Рис. 4
Любая линейная функция может быть представлена в виде композиции трех линейных функций частного вида: Отсюда заключаем, что линейное отображение общего вида (3) можно осуществить путем последовательного применения:
- 1) Поворота около начала координат на угол ; 2) Преобразования подобия с центром подобия в точке и коэффициентом подобия ; 3) Параллельного переноса на вектор, изображающий комплексное число
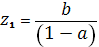
Так как каждое из трех составляющих отображений преобразует окружность в окружность, а прямую в прямую, то любое линейное отображение преобразует окружность в окружность и прямую в прямую. Его неподвижные точки можно найти из условия Отсюда при получаем и. При получаем преобразование параллельного переноса, которое имеет единственную неподвижную точку. Отметим, что при линейное отображение можно представить в виде, где z0 - неподвижная точка отображения (для этого достаточно из равенства вычесть тождество ). Из этого представления видно, что линейное отображение при представляет собой композицию поворота комплексной плоскости вокруг точки на угол и преобразования подобия (растяжения) с центром в точке и коэффициентом растяжения.
Линейное отображение определено однозначно условиями, при которых однозначно определены параметры и. Можно потребовать, чтобы две различные точки и переходили соответственно в произвольно заданные, но различные точки и. Тогда параметры и будут удовлетворять системе уравнений и, имеющей относительно и единственное решение. Соответствующее отображение имеет вид
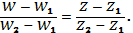
Линейное отображение будет определено однозначно и в том случае, когда в некоторой точке заданы значения функции и значения ее производной (эта производная постоянна и на самом деле не зависит от точки ). При этих условиях отображение можно записать в виде
.
Похожие статьи
-
Показательная функция - Конформное отображение
Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...
-
Дробно-линейная функция - Конформное отображение
Определение 4. Функция вида: , где - фиксированные комплексные числа, называется дробно-линейной функцией. При этом будем предполагать, что, чтобы...
-
Тригонометрические функции комплексной переменной - Конформное отображение
Определение 8. Из формулы Эйлера для всех действительных имеем Откуда , Эти формулы можно использовать для голоморфного продолжения косинуса и синуса в...
-
Конформность дифференцируемого отображения - Конформное отображение
Пусть через точку проходят две гладкие кривые и касательные l1 и l2 к которым образуют с осью углы, соответственно, 1 и 2. Образы этих кривых и при...
-
Принцип симметрии - Конформное отображение
Теорема 9 (принцип непрерывности). Пусть две односвязные области и в расширенной комплексной плоскости не пересекаются, но имеют общий участок границы в...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Инвариант дробно-линейного отображения - Конформное отображение
При помощи дробно-линейного отображения можно единственным образом преобразовать три заданные точки комплексной плоскости в три заданные комплексные...
-
Элементарные функции - Конформное отображение
Теория конформных отображений подчинена решению двух основных задач: 1) найти образ области при заданном отображении; 2) найти конформное отображение...
-
Степенная функция - Конформное отображение
Определение 6. Функция вида: , где - натуральное число, называется степенной функцией. Свойства степенных функций: 1) Функция - - дифференцируема во всей...
-
Понятие конформного отображения - Конформное отображение
Основная задача теории конформных отображений - построить конформное отображение заданной области на некоторую заданную область плоскости переменной w....
-
Сохранение симметрии при дробно-линейном отображении. - Конформное отображение
Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку, которая переходит в бесконечно удаленную точку. Если...
-
Исследуем на экстремум функцию: 1. С помощью необходимого существования экстремума, т. е. из системы Найдем координаты стационарных (критических) точек:...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
ПРАВИЛО ЛОПИТАЛЯ - Скалярные и векторные величины, матрицы и функции
Теорема Коши. Если при соблюдении предположений относительно функций и отношение стремится к некоторому числу при, то тогда к такому же числу будет...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Еще одним подходом к проблеме формализации алгоритма являются, так называемые, рекурсивные функции. Исторически этот подход возник первым, поэтому в...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Синтаксис и семантика. Теорема Райса - Рекурсивные функции
Попробуем теперь проанализировать круг проблем, неразрешимость которых доказана в предыдущем пункте. Общим для них является то, что по кодам, т. е....
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
Лемма (о декартовом произведении)., Замечания и упражнения - Рекурсивные функции
Если А - эффективное множество, то Для любого эффективного множества B AB эффективно (и, следовательно, любое декартово произведение A1A2...Аn...
-
ОБОСНОВАНИЕ ВИДА И РАСЧЕТ ПАРАМЕТРОВ АНАЛИТИЧЕСКОЙ ФУНКЦИИ - Основы прогнозирования
На практике при выборе аналитической функции рекомендуется подбирать функцию с таким расчетом, чтобы ее конструктивные элементы, коэффициенты и константы...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Ответ: Функция f называется четной если для любого х из ее области определения f(-x)=f(x) График четной функции симметричен относительно оси ординат....
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Непрерывность композиции, Точки разрыва - Свойства функций
Пусть задана функция, со значениями в, и на множестве определена функция со значениями в. Тогда для любого можно вычислить, на можно определить функцию...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
Бесконечные пределы - Свойства функций
Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...
-
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....
-
Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций
Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
Линейная функция - Конформное отображение