Тригонометрические функции комплексной переменной - Конформное отображение
Определение 8. Из формулы Эйлера для всех действительных имеем
Откуда
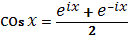
,
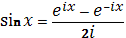
Эти формулы можно использовать для голоморфного продолжения косинуса и синуса в комплексную плоскость, положив по определению для любого :
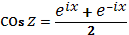
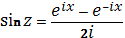
, .
Свойства тригонометрических функций комплексного переменного:
- 1) и - - дифференцируемы во всей плоскости (как линейные композиции - дифференцируемых функций). 2) и во всех точках плоскости имеют производную, причем, , . 3) Для любых справедливо: 4) Функции и имеют лишь действительные нули, а именно:
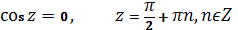
- 5) Функции и являются периодическими с основным периодом. 6) Тригонометрические функции комплексного переменного тесно связаны с гиперболическими, которые для любого определяются формулами
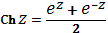
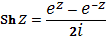
, .
Эта связь выражается соотношениями
7) Пользуясь свойствами 4) и 7) получим
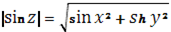
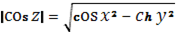
Величины и являются неограниченными, а именно вдоль мнимой оси, аналогично при
- 8) Тангенс и котангенс для комплексных значений аргумента определяются формулами 9)
Рассмотрим примеры конформных отображений осуществимых основными элементарными функциями:
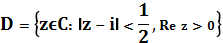
1) Построим линейное отображение, переводящее полукруг в полукруг.
Решение:
Для этого последовательно выполним следующие отображения:
1) , которое переводит область в область ;
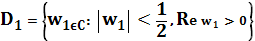
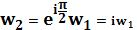
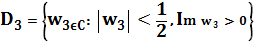
- 2) , переводящее область в полукруг ; 3) , переводящее полукруг в полукруг 4) , переводящее полукруг в.
Таким образом, получаем искомое отображение (Рис. 8)
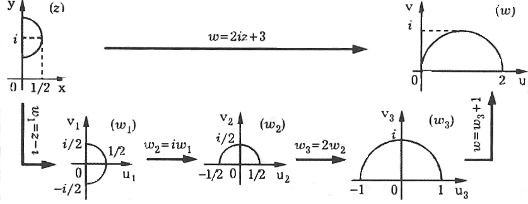
Рис. 8
2)Найти линейную функцию, отображающую треугольник с вершинами на треугольник с вершинами.
Решение:
Для того чтобы найти функцию, конформно отобразим треугольник на треугольник.
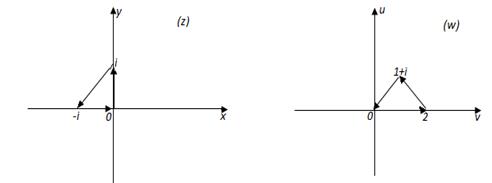
Рис. 9
Тогда вершины одного треугольника переходят в вершины другого треугольника соответственно:
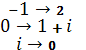
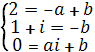
ЃЛ решим систему
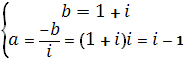
ЃЛЃЛ функция принимает вид
Проверка: , , - верное тождество.
Ответ: .
3)Найти функцию, конформно отображающую единичный круг на верхнюю полуплоскость.
Решение:
Для решения поставленной задачи установим следующее соответствие граничных точек данных областей (рис. 10):
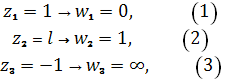
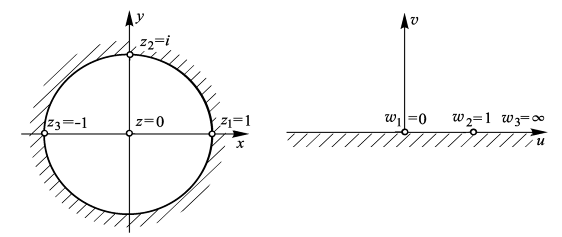
Рис. 10
И найдем коэффициенты дробно-линейной функции, осуществляющей искомое отображение. Как легко видеть из условий (1) и (2), сразу определяются значения и, после чего искомая функция принимает вид
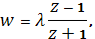
Последний коэффициент определяется из условия (2):
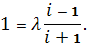
Откуда. Тем самым функция, осуществляющая искомое отображение, имеет вид
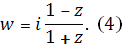
Отметим, что функция осуществляет конформное отображение области на нижнюю полуплоскость.
4) Отобразить конформно множество на множество
Решение:
Нужно найти функцию
Найдем отображение осуществимое множествами:
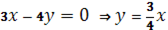
Нужно найти функцию
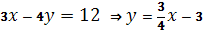
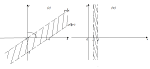
Рис. 11
1)Нужно повернуть на
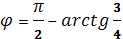
2) Ширина полосы
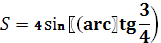
Тогда,
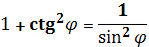
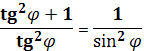
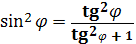
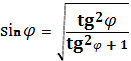
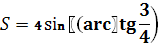
=4
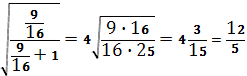
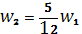
3) Сместить на 1 вправо:
Т. о.
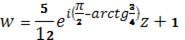
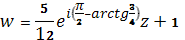
Ответ: .
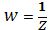
5) Отобразить конформно при помощи функции,
Решение:
Область принимает вид (Рис. 12):
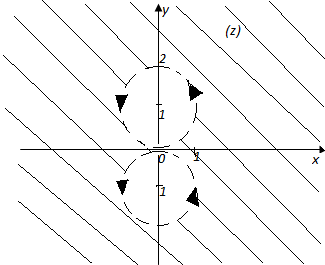
Рис. 12
Подставим крайние точки области в функцию :
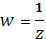
- >; >;
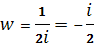
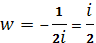
- >; >;
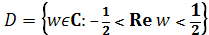
Т. о. область примет вид - (Рис. 13):
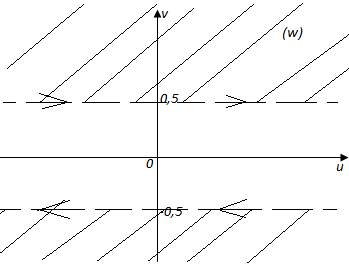
Рис.13
Ответ:
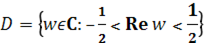
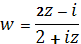
6) Выясним, на какую область отображается полукруг с помощью функции.
Решение:
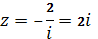
Граница области состоит из верхней полуокружности и отрезка действительной оси. Найдем образ границы. Отрезок действительной оси, не проходящее через точку, согласно замечанию 4, переходит в дугу окружности некоторого радиуса с центром в некоторой точке.
Для нахождения и в заданную функцию подставим и выделим действительную и мнимую части:
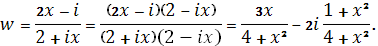
Стало быть,
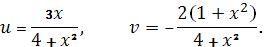
Отсюда
и
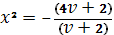
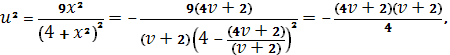
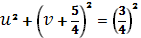
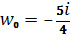
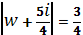
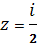
Или. Приводя это уравнение окружности к каноническому виду, устанавливаем что и. Итак, образом действительной оси будет окружность (Рис. 14). Поскольку точке полукруга соответствует точка, то область, очевидно, будет располагаться во внешности этой окружности.
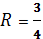
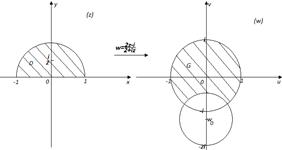
Рис. 14
Рассмотрим оставшуюся часть границы области. Образом окружности, которая не проходит через точку, согласно замечанию 4, является окружность. Чтобы установить уравнение этой окружности, в заданную функцию подставим :
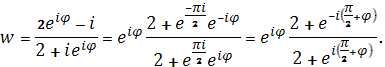
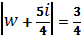
Переходя в этом равенстве к абсолютным величинам и учитывая, что числитель и знаменатель дроби справа являются комплексно сопряженными числами и их модули равны, получаем. Следовательно, образом окружности является окружность, а образом полукруга будет область, полученная пересечением внутренности окружности и внешности окружности (см. рис. 14).
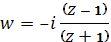
7) Найдем образ правой полуплоскости при отображении.
Решение:
Границей правой полуплоскости является мнимая ось. При заданном отображении эта ось переходит в окружность. Действительно,
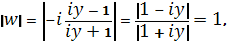
Поскольку комплексные числа и являются комплексно сопряженными, а значит, имеют равные модули.
Согласно принципу соответствия границ, образом правой полуплоскости является либо круг, либо область, так как окружность является общей границей двух областей. Взяв точку в правой полуплоскости, находим ее образ который попадает в круг. Следовательно, образом полуплоскости является круг. (Рис. 15)
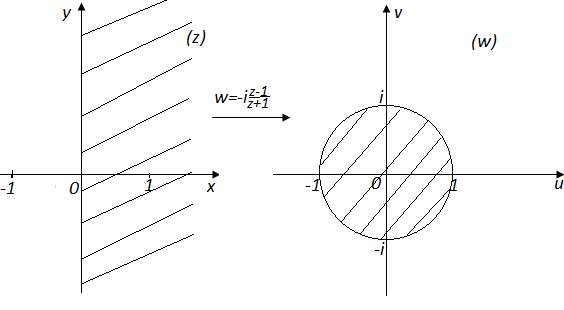
Рис. 15
8) Найдем функцию, конформно отображающую полукруг, на верхнюю полуплоскость и условии, что при.
Решение:
Рассмотрим сначала дробно-линейное отображение, переводящее три заданные граничные точки полукруга в точки и плоскости. Использую формулу (5) и учитывая замечание 3, находим
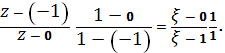
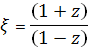
Отсюда получаем. Согласно замечанию 2, образом диаметра полукруга является действительная полуось так как ей принадлежит точки и, а образом окружности - мнимая полуось, поскольку и прямой угол между диаметром и полуокружностью в точке прямым (рис. 16). Итак, образом полукруга является первый квадрат полуплоскости, отображаемый функцией на полуплоскость В итоге получаем
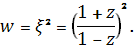
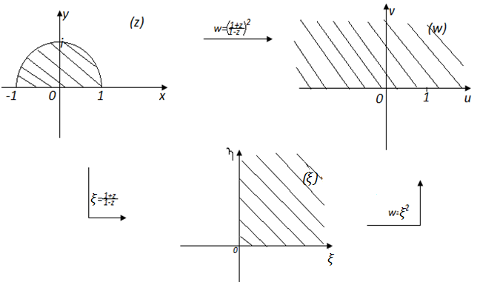
Рис. 16
9) Построим отображение луночки, ограниченной окружностями и (рис. 17), на верхнюю полуплоскость.
Решение:
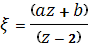
Чтобы получить искомое отображение, достаточно перевести исходную область в полосу. Итак, переведем сначала окружности и в горизонтальные прямые и соответственно. Для этого рассмотрим отображение и потребуем, например чтобы точка перешла в точку, а точка - в точку. Тогда и, и мы приходим к отображению
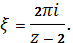
Окружности проходят через точку. Согласно замечанию 2, образами окружностей будут прямые, одна из которых проходит через точку, а другая - через точку. Так как в точке окружности, ограничивающие луночки, касаются, то прямые, в которые они переходят, параллельны. Точка, симметричная точке относительно окружности, переходит в точку, которая должна быть симметрична точке относительно образа этой окружности. Значит, образом окружности является прямая. Образом окружности будет прямая. Итак, заданная область преобразована в полосу. Осталось применить отображение. В итоге получается искомое отображение (Рис. 17)
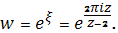
Рис. 17
Похожие статьи
-
Элементарные функции - Конформное отображение
Теория конформных отображений подчинена решению двух основных задач: 1) найти образ области при заданном отображении; 2) найти конформное отображение...
-
Показательная функция - Конформное отображение
Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...
-
Дробно-линейная функция - Конформное отображение
Определение 4. Функция вида: , где - фиксированные комплексные числа, называется дробно-линейной функцией. При этом будем предполагать, что, чтобы...
-
Степенная функция - Конформное отображение
Определение 6. Функция вида: , где - натуральное число, называется степенной функцией. Свойства степенных функций: 1) Функция - - дифференцируема во всей...
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Понятие конформного отображения - Конформное отображение
Основная задача теории конформных отображений - построить конформное отображение заданной области на некоторую заданную область плоскости переменной w....
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Инвариант дробно-линейного отображения - Конформное отображение
При помощи дробно-линейного отображения можно единственным образом преобразовать три заданные точки комплексной плоскости в три заданные комплексные...
-
Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел. Действительное число или как его еще называют...
-
Сохранение симметрии при дробно-линейном отображении. - Конформное отображение
Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку, которая переходит в бесконечно удаленную точку. Если...
-
Конформность дифференцируемого отображения - Конформное отображение
Пусть через точку проходят две гладкие кривые и касательные l1 и l2 к которым образуют с осью углы, соответственно, 1 и 2. Образы этих кривых и при...
-
Принцип симметрии - Конформное отображение
Теорема 9 (принцип непрерывности). Пусть две односвязные области и в расширенной комплексной плоскости не пересекаются, но имеют общий участок границы в...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....
-
Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Пусть R= R (sinx, cosx) является рациональной функцией. Т: Интеграл ?R (sinx, cosx) dx при помощи подстановки t=tg (x/2) [1] преобразуется в интеграл...
-
Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...
-
В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических...
-
Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...
-
Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Односторонние пределы, Пределы на бесконечности - Свойства функций
В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Табличное представление цен действий и состояний задачи имеет естественные ограничения по масштабируемости задачи на большую размерность. В дискретных...
-
Нахождение функций роста экономики региона Применив математическую модель на практике, можно узнать на сколько увеличится валовый региональный продукт,...
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Ответ: y=f(kx) получается из Графика функции f(x) сжатием его вдоль оси ох в k раз, если k>1 и растяжением в 1 деленную на k раз, если k>0 но меньше 1....
Тригонометрические функции комплексной переменной - Конформное отображение