Счетные и несчетные множества - Методы решения системы линейных уравнений
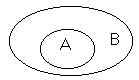
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы:
Диаграмма Венна
Диаграмма Венна
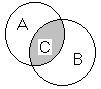
Диаграмма Венна
Диаграмма Венна
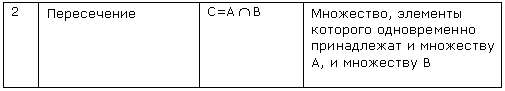
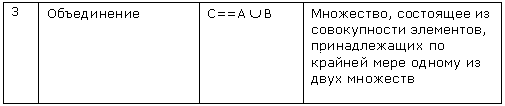
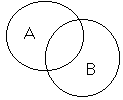

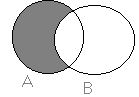
Исходя из вышеизложенного, запишем некоторые свойства множеств:
- 1. АА = 0 2. А = А 3. АА = А, АА = А 4. АВ = ВА, АВ = В А
Пределы и непрерывность
Бесконечной числовой последовательностью называется числовая функция, определенная на N натуральных чисел.
Последовательность XN называется возрастающей (убывающей), если каждый ее член, начиная со второго, больше (меньше) предыдущего, т. е. для любого n выполняется неравенство: XN+1>XN (XN+1>XN).
Последовательность XN называется невозрастающей (неубывающей), если каждый ее член, начиная со второго, не больше (не меньше) предыдущего, т. е. для любого n выполняется неравенство: XN+1?XN (XN+1?XN).
Убывающие, возрастающие, неубывающие, не возрастающие последовательности называются монотонными.
Последовательность XN называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности выполняется неравенство XN?M (XN?m). Числа М и m называются соответственно верхней и нижней границей последовательности (XN). Тот факт, что последовательность ограничена сверху числом М (снизу числом m), геометрически обозначает, что ни одна точка XN не лежит правее точки М (левее точки m).
Последовательность XN называется ограниченной, если существуют два числа М и m такие, что для всех n выполняется неравенство m?XN?M. Тот факт, что последовательность ограничена числами m и M, геометрически обозначает, что все ее члены помещаются в промежутке [m, M].
Последовательность XN называется постоянной, если все ее члены совпадают.
Обычно последовательность задается формулой, выражающей общий член последовательности через n. Иногда указывается правило, с помощью которого можно вычислить n-ый член последовательности по известным предыдущим членам. Такой способ задания последовательности называется индуктивным (или рекуррентным).
Число а называется пределом последовательности XN, если для любого е>0 все члены последовательности XN, кроме может быть, конечного их числа, лежат в е-окрестности точка а, т. е. найдется такое натуральное число N, что при n>N будет выполнено неравенство |XN-a|<е.
Последовательность может иметь только один предел. Если последовательность имеет предел, то последовательность называется сходящейся; последовательность, не имеющую предела называют расходящейся.
Если последовательность XN имеет пределом число а, то пишут. В этом случае говорят, что последовательность сходится к числу а.
Последовательность называется бесконечно малой, если ее предел равен нулю.
Число А называется пределом функции f(x) при x>a, если для любого е>0 можно указать такое д>0, что для любого x ? a, удовлетворяющего неравенству 0<|x-a|<д, выполнялось неравенство |f(x)-A|<е. В этом случае пишут.
Если число А1 (числоА2) есть предел функции y = f(x) при х, стремящемся к а так, что х принимает только значения, меньше (больше) а, то А1 (А2) называется левым (правым) пределом функции (x) в точке a. При этом соответственно пишут
Теорема 1. Если существуют пределы функций f(x) и g(x) при x>a, то существует также и предел их суммы, равный сумме пределов функций f(x) и g(x):
Теорема 2. Если существуют пределы функций f(x) и g(x) при x>a, то существует также и предел их произведения, равный произведению пределов функций f(x) и g(x):
Теорема 3. Если существуют пределы функций f(x) и g(x) при x>a, и предел функции отличен от нуля, то существует также и предел отношения f(x)/g(x), равный отношению пределов функций f(x) и g(x):
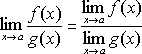
Следствие 1. Постоянный множитель можно вынести за знак предела:
Следствие 2.Если n - натуральное число, то
Следствие 3. Предел многочлена (целой рациональной функции)
При x>a равен значению этого многочлена при x = a, т. е.
Следствие 4. Предел дробно - рациональной функции
При x>a равен значению этой функции при х = а, если а принадлежит области определения функции, т. е.
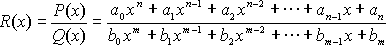
Производная и дифференциал функции.
Пусть дан график непрерывной функции Y = f(x). Возьмем на кривой y = f(x) точки M(x, y) и M(x1,y1), где x1 = x+Дx, y1 = y+Дy (где Дx - приращение аргумента, Дy - приращение функции). Проведем секущую MM1, угловой коэффициент которой обозначим через k1, т. е. k1 = tg a1. Из треугольника MM1P находим
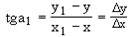
Предположим, что точка М остается неподвижной, а точка M1, перемещаясь по кривой, неограниченно приближается к М. Тогда:
- - секущая MM1 поворачивается вокруг точки М, приближаясь к положению касательной; - x1 > x, а, следовательно, Дx = (x1-x) > 0; - угол a1 стремится к углу a между касательной и осью Ox.
Пусть k Ї угловой коэффициент касательной, т. е. k = tg a. Т. к. tg a1 Ї непрерывная функция (случай, когда a1 = р/2, пока исключим из рассмотрения), то
Производной функции y = f(x) в данной точке х называют предел отношения функции Дy к соответствующему приращению аргумента Дx при условии, что Дx > 0, т. е.
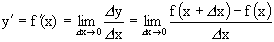
Операцию отыскания производной некоторой функции называют дифференцированием функции.
Если функция имеет производную в точке х = а, то говорят, что она дифференцируема в этой точке.
Если функция имеет производную в каждой точке длинного промежутка, то говорят, что она дифференцируема на этом промежутке.
Чтобы фактически вычислить производную данной функции необходимо проделать четыре шага, указанные в самом определении производной:
- 1. Находят новое значение функции, подставив в данную функцию вместо x новое значение аргумента: т. е. есть функция у = f(х), поставим в соответствие x > x+Дx, y > y+Дy, найдем новое значение функции y+Дy = f(x+Дx). 2. Определяем приращение функции, вычитая данное значение функции из ее нового значения 3. Составляют отношение приращения функции к приращению аргумента 4. Переходят к пределу при Дx > 0 и находят производную:
Похожие статьи
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Частные производные высших порядков - Методы решения системы линейных уравнений
Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
-
Элементарные преобразования, Миноры - Методы решения системы линейных уравнений
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...
-
1. Название проекта: "Математические модели в экономике". 2. Руководитель: учитель математики Тыкоцкая Л. И. 3. Учебные предметы: математика, экономика....
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
Счетные и несчетные множества - Методы решения системы линейных уравнений