Понятие конформного отображения - Конформное отображение
Основная задача теории конформных отображений - построить конформное отображение заданной области на некоторую заданную область плоскости переменной w.
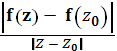
Непрерывное отображение области 2-мерного евклидова пространства в 2-мерное евклидово пространство называется конформным в точке, если оно в этой точке обладает свойствами постоянства растяжений и сохранения углов. Свойство постоянства растяжений в точке при отображении состоит в том, что отношение расстояния между образами и точек u к расстоянию между и стремится к определенному пределу, когда стремится к произвольным образом; число называется коэффициентом растяжения в точке при рассматриваемом отображении. Свойство сохранения (консерватизма) углов в точке при отображении состоит в том, что любая пара непрерывных кривых, расположенных в и пересекающихся в точке под углом б (т. е. имеющих касательные в точке, образующие между собой угол б), при рассматриваемом отображении переходит в пару непрерывных кривых, , пересекающихся в точке под тем же углом б. Непрерывное отображение области называется конформным, если оно конформно в каждой точке этой области.
По определению, конформное отображение области обязано быть непрерывным и конформным лишь во внутренних точках, и если говорят о конформном отображении замкнутой области, то, как правило, имеют в виду непрерывное отображение замкнутой области, конформное в ее внутренних точках.
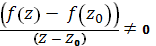
Конформные отображенияобласти 2-х мерного евклидова пространства в 2-х мерное евклидово пространство удобно рассматривать как отображение области плоскости комплексного переменного в плоскость комплексного переменного ; соответственно отображение является комплекснозначной функцией комплексного переменного. При этом если в точке отображение сохраняет углы, то криволинейные углы с вершиной при этом отображении либо сохраняют свою абсолютную величину и знак, либо сохраняют свою абсолютную величину, изменяя знак на противоположный. В первом случае говорят, что отображение в точке является конформным отображением первого рода, во втором - конформным отображением второго рода. Если функция задает конформное отображение второго рода в точке, то комплексно сопряженная функция w= задает конформное отображение первого рода в точке, и наоборот. Поэтому изучаются лишь конформные отображения первого рода, и именно их обычно имеют в виду, когда говорят о конформном отображении, не уточняя их род. Если отображение конформно в точке, то при существует конечный предел отношения, т. е. существует производная. Верно и обратное. Таким образом, если существует то каждый бесконечно малый вектор с началом в точкепри отображении преобразуется с помощью линейной функции т. е. растягивается в раз, поворачивается на угол arg и параллельно сдвигается на вектор.
В теории плоских конформных отображений и ее приложениях принципиальным является вопрос о возможности однолистно и конформно отобразить одну заданную область на другую, а в практических приложениях - вопрос о возможности это сделать посредством сравнительно простых функций. Первую задачу для случая односвязных областей, границы которых не пусты и не вырождаются в точки, решает в положительном смысле теорема Римана о конформном отображении. Вторая задача для некоторых областей специального вида, решается применением элементарных функций комплексного переменного.
Основные принципы теории конформных отображений о отображении одной области на другую
Теорема Римана. Пусть - односвязная область расширенной комплексной плоскости, граница которой содержит не менее двух точек. Тогда:
- 1) существует аналитическая в функция конформно отображающая на единичный круг 2) эту функцию можно выбрать так, что будут выполнятся условия
Где заданные точки, заданное действительное число. При этом функция условиями (1) определяются однозначно.
Две односвязные области, каждая из которых имеет не менее двух граничных точек, можно конформно отобразить одну на другую. Важным теоретическим положением, характеризующим поведение конформного отображения вблизи границы области, является следующий принцип соответствия границ.
Теорема 1. Пусть и - односвязные области, ограниченные простыми кусочно гладкими контурами и, а функция однолистно и конформно отображает область на область. Тогда:
- 1) функция, имеет непрерывное продолжение на границу области, т. е. ее можно так доопределить в точках контура, что получится функция, непрерывная в замыкании ; 2) функция, доопределяется на границе, отображает контур взаимно однозначно на контур, причем так, что положительному обходу контура будет соответствовать положительный обход контура.
Теорема 2. Пусть функция аналитична в односвязной области, ограниченной кусочно гладким контуром, и непрерывна в замыкании этой области. Если функция осуществляет взаимно однозначное отображение контура на некоторый простой кусочно гладкий контур, то отображает область конформно и однолистно на область, ограниченную контуром, причем обходу контура в положительном направлении соответствует обход контура также в положительном направлении.
Для доказательства теоремы достаточно показать, что
- 1) для каждой точки существует только единственная такая, что, т. е. функция имеет только один нуль в области ; 2) для каждой точки не существует точки такой, что т. е. функция не принимает значения ни при каком
Докажем первое утверждение. По условию теоремы функция не обращается в нуль на контуре, т. к. при точка попадает на контур, а лежит в и не может принадлежать. Значит, согласно принципу аргумента, число нулей функции в области равно
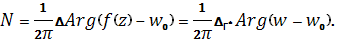
Так как точка лежит в области, ограниченной контуром, то, где знак плюс соответствует положительному направлению обхода контура. Отрицательное значение в данном случае невозможно, так как свидетельствует о наличии в области полюсов функции а по условию аналитична в Следовательно, и уравнение в области имеет только одно решение.
Рассмотрим второе утверждение. Если точка расположена во внешности контура, то и уравнение не имеет решений в области А это означает, что всякая внутренняя точка области при конформном и однолистностном отображении переходит во внутреннюю точку области. Что и требовалось доказать.
Замечание 1. Теоремы 1и 2 верны и для областей и расширенной комплексной плоскости, ограниченных простыми кусочно гладкими контурами и.
Теорема 3 (принцип сохранения области) Если функция аналитична в области и не является постоянной, то образ области также является областью.
Для доказательства теоремы требуется показать, что множество линейно связанное и открытое. Так как отображение в силу аналитичности является непрерывным отображением, то образ любого линейно связанного множества при этом отображении является линейно связанным множеством. Следовательно, линейно связанное множество.
Докажем теперь, что открытое множество, т. е. любая точка входит в вместе с некоторой своей окрестностью. Пусть один из прообразов точки. Если, то, согласно теореме об обратной функции, в некоторой окрестности точки определена функция, обратная функция к. Следовательно, все точки этой окрестности являются образами при отображении и она целиком принадлежит. Если, то к этому же выводу приходим, опираясь на теорему (Об обратной функции).
Теорема 4 (принцип максимума модуля). Если функция аналитическая в области, а ее модуль достигает локального максимума в некоторой точке, то постоянна в.
Доказательство проведем методом от противного. Пусть. Для точки выберем произвольную окрестность, целиком принадлежащую области, и предположим, что не является постоянной в рассматриваемой окрестности. Согласно принципу сохранения области, образ круга при отображении является областью. Значит, все точки некоторой окрестности точки являются образами точек круга. В этой окрестности выберем точку, для которой (если, то можно взять

,
А если, то в качестве можно взять любую точку указанной окрестности). Для этой точки имеем > Поскольку окрестность точки можно выбрать сколь угодно малого радиуса, заключаем, что точка не является точкой локального максимума функции.
Итак, если функция не является постоянной в окрестности точки, то не имеет максимума в точке. Если же достигает максимума в некоторой точке области, то функция постоянна в некоторой окрестности точки, т. е. при. Согласно теореме о единственности аналитической функции, аналитические функции и совпадают в области. Другими словами, функция постоянна в.
Теорема 5. Если функция аналитична в ограниченной области и непрерывна на замыкании этой области, то функция достигает наибольшего значения на границе области.
Действительно, если функция постоянна в, то в силу непрерывности она постоянна в и утверждение теоремы очевидно.
Если же не является постоянной в, то, согласно теореме 4, функция не может достигать наибольшего значения в области, т. к. в противном случае она имела бы в точку локального максимума. Но, будучи непрерывной на замкнутом ограниченном множестве, достигает на этом множестве своего наибольшего значения: это может произойти только на границе области.
Теорема 6. Если функция аналитична в области, не имеет в нулей и ее модуль достигает в локального минимума, то постоянна в этой области.
Теорема 7 (лемма Шварца). Если аналитическая в круге функция удовлетворяет условиям, , то и, z. При этом равенство или возможно хотя бы в одной точке z0 лишь тогда, когда
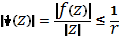
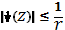
Доказательство. В силу того, что точка является нулем функции, эту функцию можно представить в виде, где - аналитическая функция в, причем. Рассмотрим круг, ограниченный окружностью Функция аналитична в и непрерывна в. Поэтому, согласно теореме 5, она достигает наибольшего значения на границе. При этом при, так как по условию теоремы. Следовательно, всюду в имеем.
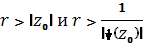
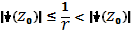
Предположим, что в некоторой точке выполнено неравенство. Выберем r<1 так, что. Тогда и, следовательно, . Получили противоречие, которое показывает, что на самом деле всюду в. В частности, в.
Если, то функция достигает максимума в точке, равного единице. Аналогично равенство означает, что достигает максимума в точке, равного единице. И в том и в другом случае, согласно принципу максимума модуля, функция является постоянной, причем. Следовательно, и.
Теорема 8. Пусть функция гармоническая в ограниченной области и непрерывная в замыкании этой области. Если непостоянна в, то она достигает наибольшего и наименьшего значений только на границе этой области.
Похожие статьи
-
Тригонометрические функции комплексной переменной - Конформное отображение
Определение 8. Из формулы Эйлера для всех действительных имеем Откуда , Эти формулы можно использовать для голоморфного продолжения косинуса и синуса в...
-
Элементарные функции - Конформное отображение
Теория конформных отображений подчинена решению двух основных задач: 1) найти образ области при заданном отображении; 2) найти конформное отображение...
-
Конформность дифференцируемого отображения - Конформное отображение
Пусть через точку проходят две гладкие кривые и касательные l1 и l2 к которым образуют с осью углы, соответственно, 1 и 2. Образы этих кривых и при...
-
Принцип симметрии - Конформное отображение
Теорема 9 (принцип непрерывности). Пусть две односвязные области и в расширенной комплексной плоскости не пересекаются, но имеют общий участок границы в...
-
Показательная функция - Конформное отображение
Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...
-
Инвариант дробно-линейного отображения - Конформное отображение
При помощи дробно-линейного отображения можно единственным образом преобразовать три заданные точки комплексной плоскости в три заданные комплексные...
-
Дробно-линейная функция - Конформное отображение
Определение 4. Функция вида: , где - фиксированные комплексные числа, называется дробно-линейной функцией. При этом будем предполагать, что, чтобы...
-
Степенная функция - Конформное отображение
Определение 6. Функция вида: , где - натуральное число, называется степенной функцией. Свойства степенных функций: 1) Функция - - дифференцируема во всей...
-
Сохранение симметрии при дробно-линейном отображении. - Конформное отображение
Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку, которая переходит в бесконечно удаленную точку. Если...
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
На уровне общества для описания поведения потребителей вводится целевая функция потребления. Целевая функция потребления - функция, выражающая уровень...
-
Например, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима...
-
ПОНЯТИЕ ЭЛЕКТРОЛИЗА - Электролиз и его практическое применение
Электролизом называют окислительно-восстановительный процесс, протекающий на электродах при прохождении электрического тока через раствор или расплав...
-
Основные понятия линейного программирования - Оптимальное программирование
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. При...
-
Если на равновесную с-му не оказ-ся вноешнего воздействия (не изм. темп, давл.), то равновесие м/существовать неизменным долго. Любое внешнее возд-ие...
-
Понятие числовой последовательности - Свойства функций
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Понятие квантовой химии - Квантовые концепции в химии
Квантовая химия - это раздел теоретической химии, в котором строение и свойства химических соединений, их взаимодействие и превращение в химических...
-
С кислородом большинство металлов образует оксиды - амфотерные и основные: 4Li + O2 = 2Li2O, 4Al + 3O2 = 2Al2O3. Щелочные металлы, за исключением лития,...
-
Ключевые понятия и определения Для дальнейшей работы приведем некоторые термины и классификации, характерные для рынка коммерческой недвижимости....
-
Основные понятия и отношения - Системная революция и принцип дуального управления
Все структурные образования и процессы, с которыми приходится иметь дело в систематике, существуют в самых различных по своей природе пространствах...
-
Пусть { , , ..., } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном...
-
В данной главе мы обсуждаем известные модели НС: модель Маккалоха и Питтса; модель Розенблата; модели Хопфилда и Больцмана; модель на основе обратного...
-
Основные понятия и определения проблемы прогнозирования - Прогнозирующие системы
Необходимо отметить, что мы рассматриваем прогнозирование в целях планирования производства или управления запасами. Таким образом, наш интерес лежит в...
-
Понятие и применение графа рынка - Использование квази-клик для анализа графа рынка России
Динамика характеристик отражающих тенденцию поведения фондового рынка может быть интересна многим участникам фондовой биржи и, в особенности, инвесторам....
-
Скорость реакции определяется изменением молярной концентрации одного из реагирующих веществ: V=dC/dtV. Факторы, влияющие на скорость химических...
-
Программа статистического наблюдения - Статистика: ее понятия и особенности наблюдения
Программа статистического наблюдения. Всякое явление обладает множеством различных признаков. Собирать информацию по всем признакам нецелесообразно, а...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Электролиз - р-ция превращения ве-ва под действ. эл. тока. если к р-ру или расплаву эл-та поднести эл. ток, то ионы в нем начнут направленно перемещаться...
-
Определение понятия "имитационное моделирование" - Имитационное моделирование в экономике
В современной литературе не существует единой точки зрения по вопросу о том, что понимать под имитационным моделированием. Так существуют различные...
-
Гидролиз - р-ция обменного взаимод-я ионов связи, с ионами, входящими в состав Н2О (Н+ и ОН-). Г-з протекает в том случае, если хотя бы один из ионов...
-
ЗАКЛЮЧЕНИЕ - Понятие и виды логистической системы
Информационные системы обеспечивают подготовку, ввод, хранение, обработку, контроль и передачу данных. Они представляют собой соответствующие...
-
Модель в общем смысле (обобщенная модель) есть создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа,...
-
Понятие "показатель асимметрии", Понятие "показатель эксцесса" - Математическая статистика
Когда график вариационного ряда (распределение набора данных) скошен в правую сторону больше, чем в левую, то мы говорим, что распределение имеет...
-
Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл
Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...
-
Кокаин, Понятие кокаина - Кокаин и новокаин
Понятие кокаина КОКАИН (Сосаinum). Алкалоид, содержашийся в листьях южно-американского растения (кустарника) Еrythroxylon coca. В медицинской практике...
Понятие конформного отображения - Конформное отображение