Принцип симметрии - Конформное отображение
Теорема 9 (принцип непрерывности). Пусть две односвязные области и в расширенной комплексной плоскости не пересекаются, но имеют общий участок границы в виде простой кусочно гладкой дуги. Если функция аналитична в области и непрерывна на множестве а функция 2 (z) аналитична в и непрерывна на множестве, причем при, то функция
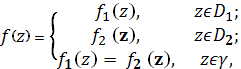
Аналитична в области
Определение 1. Пусть выполнены следующие условия:
- 1) Функция определена на множестве ; 2) Функция аналитическая в области ; 3) при.
Тогда функцию называют аналитическим продолжением функции.
Теорема 10 (принцип симметрии). Пусть - односвязная область, лежащая в верхней полуплоскости, граница которой содержит интервал действительной оси, а область, симметричная этой оси. Если функция непрерывна в области и на ее границе, аналитична в и принимает действительные значения при то эту функцию можно аналитически продолжить в область по формуле
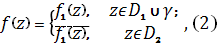
Доказательство. Рассмотрим в области функцию =. Эта функция корректно определена, так как для любой точки точка принадлежит области. Докажем, что является аналитической в. Рассмотрим произвольную точку и некоторую ее окрестность, целиком попадающую в. Тогда окрестность целиком попадает в и в ней в силу аналитичности функцию можно разложить в ряд Тейлора:
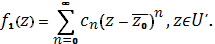
Пусть. Тогда, и мы имеем
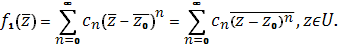
Следовательно,
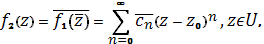
Т. е. в окрестности точки функция представима степенным рядом, а потому аналитична. Так как можно выбрать произвольно, то аналитична всюду в.
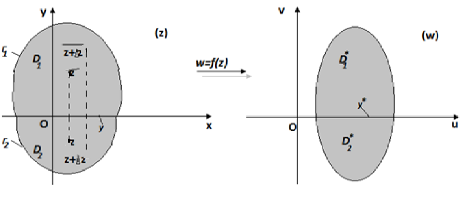
Рис.1.
Функция, определяемая соотношением (2), непрерывна в областях и т. к. в этих областях функции и аналитичны (а потом и непрерывны). Покажем, что функция непрерывна и в точках интервала. Возьмем произвольную точку (рис.1.). В силу непрерывности функции в точке для любого можно выбрать такое, что для точек удовлетворяющих неравенству, верно неравенство.
Отметим, что по условию теоремы значение является действительным. Для произвольной точки, для которой, имеем либо, либо. В первом случае в силу выбора верно соотношение, тогда и. Во втором случае получаем
Т. к. точка попадает в область и для нее. Итак, для любого существует такое, что при и верно неравенство. Это означает, что функция непрерывна в точке, а в силу произвольности выбора она непрерывна на всей дуге.
Применяя принцип непрерывности (см. теорему 9), заключаем, что функция является аналитической в области, т. е. являются, согласно определению 1, аналитическим продолжением функции из области в область.
Похожие статьи
-
Понятие конформного отображения - Конформное отображение
Основная задача теории конформных отображений - построить конформное отображение заданной области на некоторую заданную область плоскости переменной w....
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Элементарные функции - Конформное отображение
Теория конформных отображений подчинена решению двух основных задач: 1) найти образ области при заданном отображении; 2) найти конформное отображение...
-
Тригонометрические функции комплексной переменной - Конформное отображение
Определение 8. Из формулы Эйлера для всех действительных имеем Откуда , Эти формулы можно использовать для голоморфного продолжения косинуса и синуса в...
-
Показательная функция - Конформное отображение
Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...
-
Инвариант дробно-линейного отображения - Конформное отображение
При помощи дробно-линейного отображения можно единственным образом преобразовать три заданные точки комплексной плоскости в три заданные комплексные...
-
Дробно-линейная функция - Конформное отображение
Определение 4. Функция вида: , где - фиксированные комплексные числа, называется дробно-линейной функцией. При этом будем предполагать, что, чтобы...
-
Степенная функция - Конформное отображение
Определение 6. Функция вида: , где - натуральное число, называется степенной функцией. Свойства степенных функций: 1) Функция - - дифференцируема во всей...
-
Конформность дифференцируемого отображения - Конформное отображение
Пусть через точку проходят две гладкие кривые и касательные l1 и l2 к которым образуют с осью углы, соответственно, 1 и 2. Образы этих кривых и при...
-
Сохранение симметрии при дробно-линейном отображении. - Конформное отображение
Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку, которая переходит в бесконечно удаленную точку. Если...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Принципы получения гибридных соединений на основе квантовых точек и органических хромофоров В литературе для получения соединений, обладающих...
-
Принципы декомпозиционного анализа экономической системы
Принципы декомпозиции Декомпозиция исходной системы или глобальной задачи производится путем применения принципов декомпозиции и координации. Первые...
-
Свойства элементов - Системная революция и принцип дуального управления
Ранее мы уже говорили о том, что при вхождении в состав системы элемент приобретает некоторые новые свойства, которыми он раньше не обладал, и теряет...
-
Информационно-статистическая теория голосований - Системная революция и принцип дуального управления
Социально-экономические системы относятся к классу больших систем. Это - системы, состоящие из достаточно большого числа примерно равносущественных для...
-
Ценообразование при рыночной власти - Принцип ценообразования при рыночной власти
Рассмотрим условия нахождения оптимальной цены и объема производства монополиста при обычных условиях рынка и найдем прибыль от полученных данных. Для...
-
Функциональные свойства систем - Системная революция и принцип дуального управления
Функциональная полнота системы определяет степень соответствия системы функций, выполняемых системой, множеству функций, выполнение которых необходимо с...
-
Моделирование бизнес процессов основывается на ряде принципов, которые дают возможность создать адекватные модели процессов. Их соблюдение позволяет...
-
В данном случае анализируемые системы характеризуются не одним набором показателей эффективности, а несколькими: (18) Где - группа показателей...
-
Горение в техногенных устройствах и горение при техногенных пожарах - Принципы горения и взрыва
Техногенная опасность - состояние, внутренне присущее технической системе, промышленному или транспортному объекту, реализуемое в виде поражающих...
-
Введение - Принцип ценообразования при рыночной власти
Монополизация отраслей представляет собой серьезную проблему переходной экономики, предприятия - монополисты обладают существенными рыночными...
-
Проба брал на ГПУ г. Москвы "Природный заказника "Воробъевы горы"из реки Москва, с помощью стеклянной бутыли. Затем стеклянную бутыль опускал в реку и...
-
Принципы измерения цвета - Основные колориметрические системы
Для воспроизведения цвета необходимо знать характеристики как воспроизводимого объекта, так и полученного результата (например, цветной оригинал и его...
-
Уравнение реакции горения вещества в воздухе составляется с учетом того, что в нем на 1 моль кислорода приходится 3,76 молей азота. Например, реакции...
-
СПОСОБЫ ОПИСАНИЯ СТРУКТУР. МОРФОЛОГИЯ СОЦИАЛЬНО-ПОЛИТИЧЕСКОЙ И ЭКОНОМИЧЕСКОЙ СФЕР Структурное моделирование. Структурный анализ Основная цель...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Ценностная окраска ситуационных образов, возникающих в сознании членов человеческого сообщества, является основным движущим стимулом, формирующим их...
-
Прагматические свойства информации - Системная революция и принцип дуального управления
Если семантические свойства информации отражают ситуационный аспект существования системы (осмысленность, оформленность ее бытия), то прагматические...
-
Опыт проводили в условиях, имитирующих периодическую экстракцию: в стакан одновременно загружали все реагенты и перемешивают их в течение заданного...
-
Актуальность темы. В современных условиях глобальной конкуренции на все более интегрирующихся мировых рынках, развитие химической промышленности...
-
Реакторами идеального (полного) смешения называются реакторы непрерывного действия, в которых осуществляется турбулентный гидродинамический режим. В них...
-
С системной точки зрения важно иметь в виду, что мы оцениваем вещи, явления или события не сами по себе, а в их ситуационном проявлении, т. е. по их...
-
Понятие государственного бюджета. Принципы бюджетной системы Центральное место в финансовой системе любого государства занимает государственный бюджет -...
-
Квантификация - Системная революция и принцип дуального управления
Одной из главных идей системно-физического подхода является идея измеримости признаков, используемых для описания реальной действительности. Оценка...
-
Факторы - Системная революция и принцип дуального управления
Возникновение системы и ее существование в определенных пространственно-временных масштабах связаны в конечном счете с действием различного рода...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
Живая система - совокупность взаимодействующих элементов, которая образует целостный объект, имеющий новые качества, не свойственный входящим в систему...
-
Эйнштейн решил теорию относительности при изучении эффектов электрического и магнитного полей, а также при скоростях движения тел, близких к скорости...
-
Влажность, летучие продукты пиролиза и межфазовые переходы - Принципы горения и взрыва
Пиролиз (от греч. руr-огонь и lysis-разложение, распад) - разложение или др. превращения хим. соединений при нагревании. Образование пламени связано с...
Принцип симметрии - Конформное отображение