Теоремы о пределах, По &;nbsp;теореме&;nbsp; о связи &;nbsp;предела&;nbsp; и бесконечно малой функции: - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

Теорема 1. Предел постоянной равен самой постоянной.

.

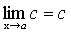
Доказательство. f(x)=с, докажем, что

.

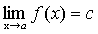
Возьмем произвольное e>0. В качестве d можно взять любое

Положительное число.

Тогда при

.

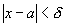
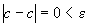
Теорема 2. Функция не может иметь двух различных пределов водной точке.

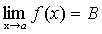
Доказательство. Предположим противное. Пусть

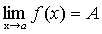
и.

По теореме о связи предела и бесконечно малой функции:

F(x)-A= - б. м. при,

F(x)-B= - б. м. при.

Вычитая эти равенства, получим:

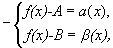
B-A=-.

Переходя к пределам в обеих частях равенства при, имеем:

B-A=0, т. е. B=A. Получаем противоречие, доказывающее теорему .

Теорема 3. Если каждое слагаемое алгебраической суммы функцийимеет предел при, то и алгебраическая сумма имеет предел при, причем предел алгебраической суммы равен алгебраической сумме пределов.

.

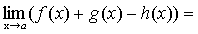
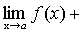
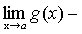
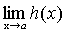
Доказательство. Пусть

, , .

Тогда, по теореме о связи предела и б. м. функции:

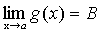
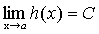
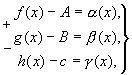
Где - б. м. при.

Сложим алгебраически эти равенства:

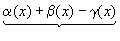
F(x)+g(x)-h(x)-(А+В-С)=,

Где б. м. при.

По теореме о связи предела и б. м. функции:

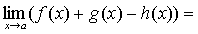
А+В-С=.

Теорема 4. Если каждый из сомножителей произведения конечного числа функций имеет предел при, то и произведение имеет предел при, причем предел произведения равен произведению пределов.

.

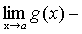
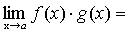
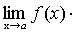
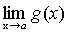
Следствие. Постоянный множитель можно выносить за знак предела.

.

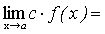
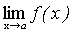
Теорема 5. Если функции f(x) и g(x) имеют предел при,

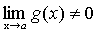
Причем, то и их частное имеет предел при, причем предел частного равен частному пределов.

, .

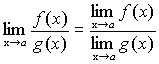
Похожие статьи

• Действия над комплексными числами в алгебраической форме, Четность и нечетность функции, Монотонность и периодичность функции, Предел функции в точке - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...

• Тригонометрические функции половинного аргумента, Обратные тригонометрические функции и их свойства, Частные случаи решения тригонометрических уравнений - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...

• Радианная и градусная меры углов, Тригонометрические функции числового аргумента - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...

• Логарифмы, Формулы и свойства логарифмов - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...

• О периодических функциях - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....

• Действительные числа, Комплексные числа - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел. Действительное число или как его еще называют...

• Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений

  Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...

• Бесконечные пределы - Свойства функций

  Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...

• 7. ПРЕДЕЛ ФУНКЦИИ, ПОНЯТИЕ ФУНКЦИИ, ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ - Скалярные и векторные величины, матрицы и функции

  ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...

• Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций

  Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....

• Понятие числовой последовательности - Свойства функций

  Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...

• О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...

• Интегрируемость непрерывных, разрывных и монотонных функций, Основные свойства определенного интеграла - Определенные интегралы

  Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...

• Решение квадратных уравнений, Решение квадратных неравенств, Числовая функция и способы ее задания - Математика в современном мире

  Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....

• Частные производные высших порядков - Методы решения системы линейных уравнений

  Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...

• Счетные и несчетные множества - Методы решения системы линейных уравнений

  Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...

• Введение, Формулировка теоремы, Обозначения, Доказательство вспомогательных лемм - Об одной теореме теории чисел

  В данной работе доказывается методами элементарной математики "большая" или "последняя" теорема Ферма. Некоторая, излишняя в обычных случаях, подробность...

• Функция y=arccosx, ее график, свойства, Функция y=arctgx, ее график, свойства, Функция y=arcctgx, ее график, свойства, Решение уравнений sinx=a, частные случаи, Решение уравнений cosx=a, частнае случаи, Решение уравнений tgx=a, ctg=a, Решение тригонометрических уравнений, приводимых к квадратным, Решение простейших тригонометрических неравенств, Стереометрия. Основные понятия, обозначения, Аксиомы стереометрии - Математика в современном мире

  Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...

• Сложная функция, Cхема исследования функции по графику, Тригонометрические функции числового аргумента, Перевод градусной меры угла в радианную и наоборот - Математика в современном мире

  Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...

• Бесконечный предел, Замечательные пределы - Свойства функций

  Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно...

• Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач

  Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...

• Разложение правильной рациональной дроби на сумму простейших дробей. - Методы решения системы линейных уравнений

  Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...

• Односторонние пределы, Пределы на бесконечности - Свойства функций

  В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что, то получают Односторонний...

• Доказательство теоремы - Об одной теореме теории чисел

  Доказательство теоремы проводится отдельно для случая, когда (т. е. показатель степени в равенстве (2) - НЕЧЕТНОЕ число) и когда (т. е. показатель...

• Непрерывность функции - Свойства функций

  Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...

• Дифференциальные уравнения - Неопределенный интеграл

  Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...

• Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций

  Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....

• Теоремы Ферма, Ролля, Лагранжа и Коши

  Введение В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи...

• ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы

  Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...

• Векторы, и образуют правую тройку векторов. - Сферический треугольник и его применение

  Свойства: 1. 2. 3. 4. 13. Смешанное произведение векторов и его свойства . Смысл смешенного произведения: сначала два вектора векторно перемножают, а...

• Определение определенного интеграла - Определенный интеграл

  Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...

• Основные тригонометрические тождества, Знаки значений тригонометрических функций, Таблица значений, Формулы сложения, Формулы двойного аргумента, Формулы половинного аргумента, Формулы приведения, Формулы синусов и разности синусов (косинусов), График функции у=sinx и его свойства, График функции y=cosx и его свойства, График функции y=tgx и его свойства, График функции y=ctgx и его свойства, Функция y=arcsinx, ее график, свойства - Математика в современном мире

  Ответ: 2) 3) 4) Знаки значений тригонометрических функций Ответ: Sin cos tg*ctg Таблица значений Ответ: Формулы сложения Ответ1 Формулы двойного...

• Функции и ее свойства - Методы решения системы линейных уравнений

  В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...

• Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля - Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля

  Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...

• Производной. - Методы решения системы линейных уравнений

  Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...

• МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ, МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ, СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ. - Скалярные и векторные величины, матрицы и функции

  МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...

• Элементы матричного анализа - Методы решения системы линейных уравнений

  Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...

• Алгебраические дополнения, Обратная матрица, войства обратных матриц. - Методы решения системы линейных уравнений

  Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...

• Системы линейных уравнений - Методы решения системы линейных уравнений

  Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...

• Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел

  Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...

Теоремы о пределах, По &;nbsp;теореме&;nbsp; о связи &;nbsp;предела&;nbsp; и бесконечно малой функции: - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

Предыдущая | Следующая