ОБОСНОВАНИЕ ВИДА И РАСЧЕТ ПАРАМЕТРОВ АНАЛИТИЧЕСКОЙ ФУНКЦИИ - Основы прогнозирования
На практике при выборе аналитической функции рекомендуется подбирать функцию с таким расчетом, чтобы ее конструктивные элементы, коэффициенты и константы поддавались экономической интерпретации, а линия тренда отображала наиболее характерное изменение признака.
Наиболее широко используются следующие функции:
- 1. линейная: yT =a+bt, где а и b - константы 2. параболическая: yT =a+bt+ct2 , где а, b, с - константы 3. степенная: yT =atB 4. экспоненциальная: yT =aT 5. гиперболическая: yT =a+ 6. простая модифицированная экспоненциальная функция: yT =a-bT 7. логистическая: yT =
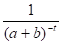
Расчет коэффициентов трендов может быть произведен несколькими способами, но наибольшее распространение получил метод наименьших квадратов.
Аналитическая функция yT является наиболее точно отображающей зависимость исследуемого признака, если соблюдается условие:
(yT-)2 min (1)
В данном случае yT и t являются известными величинами, а неизвестными являются параметры уравнения =f(t). Для их поиска необходимо приравнять к 0 части произ-водные уравнения (1) по каждой искомой константе к нулю.
После соответствующих преобразований получим систему уравнений, которую называют нормальной.
Для случая линейной функции yT =a+bt система нормальных уравнений будет иметь вид:
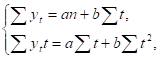
Где n - число членов динамического ряда.
Решив данную систему, найдем параметры а и b в уравнении yT =a+bt. Можно осуществить прогноз, если будем подставлять вместо t порядковый номер искомого периода.
Однако не во всех случаях используется линейное уравнение. При использовании нелинейного уравнения для построения системы нормальных уравнений применяется следующее правило, которое рассмотрим на примере параболической зависимости:
1. запишем уравнение регрессии в общем виде:
=a+bt+ct2;
2. выделим искомые параметры:
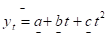
;
3. для построения 1-го нормального уравнения свободный член умножается на n, перед всеми остальными проставляется знак
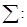
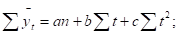
4. для построения 2--го нормального уравнения и последующих в зависимости от количества констант, все члены уравнения умножаются на t.
В том случае, если в качестве функции yT используются логистическая, экспериментальная и гиперболическая и др. зависимости, то перед построением системы нормальных уравнений их необходимо привести к линейному виду. Способы линизации нелинейных функций приведены в таблице 2.1.
Таблица 2.1
Способы линизации нелинейных функций
|
Функция |
Исходное уравнение |
Способ линизации |
Линейное уравнение |
|
1 |
2 |
3 |
4 |
|
Гиперболическая |
YT =a+ | 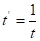
YT =a+bt | |
|
Степенная |
YT =atB |
LnyT=lna+blnt, LnyT=y'T, Lna=a', Lnt=t |
Y'T =a,+bt' |
|
Экспоненциальная |
YT =aT |
LnyT=lna+t, LnyT=y'T, Lna=a' |
Y,T =a'+t |
|
Простая Модифицированная экспоненциальная Функция |
YT =a-b-t |
E-t=t' |
YT =a-bt |
|
1 |
2 |
3 |
4 |
|
Логистическая |
YT = | 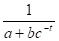
, , E-t=t' |
Y'T =a+bt |
Похожие статьи
-
МЕТОДЫ ИСКЛЮЧЕНИЯ АВТОКОРРЕЛЯЦИИ ИЗ РЯДОВ ДИНАМИКИ - Основы прогнозирования
Для исключения автокорреляции могут применяться следующие методы: 1. метод конечных разностей; 2. метод исключения тенденций с помощью уравнений...
-
При использовании статистических методов прогнозирования во многих случаях необходимо знать возможную ошибку прогноза, т. е. тот интервал, в котором...
-
В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических...
-
Методы оценки параметров структурной формы модели - Основы эконометрики
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Нелинейный регрессионный анализ, Множественный регрессионный анализ - Основы научных исследований
Линейные по параметрам регрессионные модели можно использовать для аппроксимации нелинейных зависимостей путем их линеаризации с помощью базисных...
-
Постановка задачи регрессионного анализа - Основы научных исследований
Основное назначение Регрессионного анализа (РА) - получение по экспериментальным данным зависимостей, аппроксимирующих эти данные в виде алгебраических...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
В данной главе описан способ прогнозирования с помощью НС, основанный на методе окон. Также приведен обзор применения НС в финансовой сфере. Общий подход...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системе нечеткого вывода Сугено. Вывод осуществляется за два...
-
Параметры эмпирических распределений - Основы научных исследований
По опытным (эмпирическим) данным строятся распределения исследуемых случайных величин. Функции плотности Р(х) таких распределений могут иметь один...
-
Множественная регрессия - уравнение связи с несколькими независимыми переменными: где - зависимая переменная (результативный признак); - независимые...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Квадранты МОБ. Пример расчета МОБ - Многосекторные модели прогнозирования
Балансовая модель производства является одной из наиболее простых математических моделей. Она записывается в виде системы уравнений, каждое из которых...
-
1. Прогнозирование по среднему приросту осуществляется по формуле: Где t - порядковый номер периода; у0 - начальный уровень ряда; - средний абсолютный...
-
Задачей данного раздела курсового проекта является определение потоков мощности по линиям выбранного варианта электрической сети и напряжений на шинах...
-
ПОНЯТИЕ ОБ АВТОКОРРЕЛЯЦИИ. ОПРЕДЕЛЕНИЕ СИЛЫ АВТОКОРРЕЛЯЦИИ Парные регрессионные модели отражают специфику взаимодействия некоторого функционального...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
МЕТОДЫ ОТБОРА СПЕЦИАЛИСТОВ В ЭКСПЕРТНУЮ ГРУППУ - Основы прогнозирования
Проведение экспертизы начинается с создания специальной группы специалистов-организаторов опроса. Задачами группы являются выбор цели экспертизы,...
-
Главным параметром трансформатора является его мощность. Различают электромагнитную, полезную, расчетную и типовую мощности трансформатора....
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
Оценим величину экономического эффекта от применения преобразователя частоты Lenze SMD ESMD223L4TXA (цена со склада в Петербурге 37 000 р. с НДС) на...
-
Среди различных конфигураций искусственных нейронных сетей встречаются такие, при классификации которых по принципу обучения, строго говоря, не подходят...
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Термодинамическая система - это тот объект, который изучает техническая термодинамика. (изотермические, изобарные, изохорные) Термодинамические системы...
-
Аппроксимация функции предпочтения ЛПР нейронными сетями имеет в работе ту особенность, что процесс обучения нейронных сетей происходит в условиях малой...
-
Горючие системы Подразделяются на однородные и неоднородные. Однородными являются системы, в которых горючее вещество и воздух равномерно перемешаны друг...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Собственно-корреляционные параметрические методы изучения связи - Основы эконометрики
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка...
-
Парная регрессия на основе метода наименьших квадратов и метода группировок - Основы эконометрики
Парная регрессия Характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями: Прямой...
-
Зависимость скорости реакции от температуры определяется правилом Вант-Гоффа : При повышении температуры на каждые 10о скорость большинства реакций...
-
Ранговый метод оценивания параметров регрессионной модели
Пример кода, вычисляющий результаты эксперимента по сравнинию ранговой оценки, МНК - и МНМ-оценок параметров для модели с гауссовским распределением...
-
Построение теоретической функции методом наименьших квадратов Задание 1 Используя метод наименьших квадратов найти оценки коэффициентов регрессионной...
-
ТЕМПЕРАТУРА - Основные положения молекулярно-кинетической теории, ее опытные обоснования
Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой. Тепловое или термодинамическое равновесие - такое...
-
Введение, Методы экстраполяции - Формализованные методы прогнозирования
К формализованным методам относятся методы экстраполяции и методы моделирования. Они базируются на математической теории. Среди методов экстраполяции...
-
Проблема идентификации - Основы эконометрики
При переходе от приведенной формы модели к структурной эконометрии сталкивается с проблемой идентификации. Идентификация - это единственность...
-
Получим систему линейных уравнений: Уравнение гиперболической регрессии: Добавим на диаграмму рассеяния линию гиперболического тренда. Рисунок 9 Вычислим...
ОБОСНОВАНИЕ ВИДА И РАСЧЕТ ПАРАМЕТРОВ АНАЛИТИЧЕСКОЙ ФУНКЦИИ - Основы прогнозирования