Уравнение Пелля и диофантовые уравнения
С помощью алгебраических чисел получены явные выражения и нелинейные рекуррентные соотношения для решений диофантовых уравнений, что позволило найти простое решение диофантова уравнения В приложении показана возможность обобщения данного подхода.
Пелль диофантовый алгебраический рекуррентный
With algebraic numbers we have evident representations and nonlinear recurrent correlations for solutions of diophantine equitions, and that is the way to find the simple solution of diophantine equition In appendix we demonstrate possibility for present approach generalization.
Уравнение Пелля и уравнение
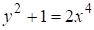
В 1942 г. Люнгрен (Ljunggren W.) получил решение уравнения, которое было настолько сложным, что покойный профессор Морделл ( Mordell L. J.) утверждал: " Трудно вообразить более сложное решение, и можно только желать его упрощения." 3. Последующие упрощения решения 3,4 все же использовали изощренные математические методы и сложные вычисления.
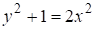
При этом не учитывалось, что данное уравнение является частным случаем уравнения, которое связано с уравнением Пелля.
Уравнение Пелля является одним из наиболее изученных диофантовых уравнений. Весьма подробное изложение истории исследования этого уравнения имеется в 1. Далее будем рассматривать только решения в натуральных числах, и если найдено начальное решение уравнения Пелля то бесконечная последовательность всех решений может быть найдена из соотношения 2, стр.341.
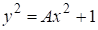
Для простоты рассмотрим случай, при необходимости последующее изложение несложно обобщить для произвольного натурального Известно, что решения можно получить из рекуррентной цепочки равенств 1,стр.43
(1)
Четные значения n дают решения уравнения Пелля, т. е. Нечетные значения n дают решения уравнения
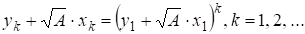
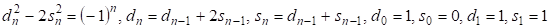
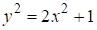
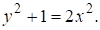
Удобно использовать алгебраические числа
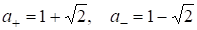
(2)
С их помощью соотношения (1) представим в виде
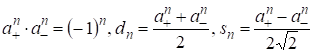
(3)
Отсюда можно получить нелинейные рекуррентные формулы для решений уравнения Пелля
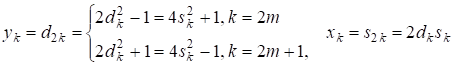
(4)
Непосредственной проверкой несложно с помощью (3) установить нелинейные рекуррентные формулы для решений уравнения
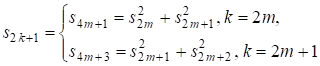
(5)
Соотношения (5) позволяют получить довольно простое решение диофантова уравнения В соответствии с (5) решения этого уравнения должны удовлетворять соотношениям пифагоровой тройки, т. е. возможны:
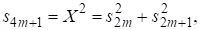
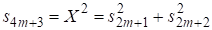
2 случай а) и случай б): .
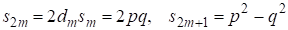
Действительно, из соотношений (1-3) следует, что и эти числа взаимно простые. Поэтому для случая а) с учетом (4) должно выполняться условие для пифагоровой тройки, где и имеют разную четность. Тогда из первого условия следует, что четное, т. к. всегда нечетно, а четно при четном. При этом из (1) следует
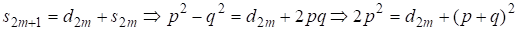
(6)
В соответствии с (4) для четного m получим из (6)
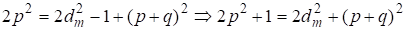
(7)
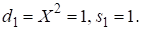
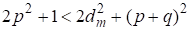
Из уравнения (7) видим, что решение возможно, если В простейшем случае Это соответствует начальному решению (1) Но это решение не относится к пифагоровым тройкам, т. к. для них При уравнение (7) не имеет решения, т. к. .
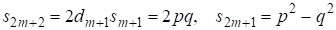
Аналогично рассмотрим случай б), и с учетом (4) условие для пифагоровой тройки имеет вид: при четном Из соотношений (1) или (3) нетрудно вывести, что Теперь получим условия существования решения
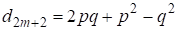
(8)
Для четных с учетом (4) из этого следует
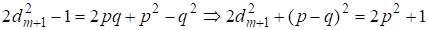
(9)
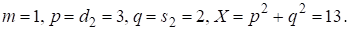
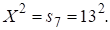
Очевидное решение (10) при соответствует Далее с учетом (5) находим, что Используя (3)
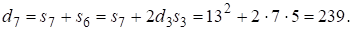
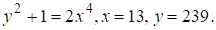
Таким образом имеем второе решение уравнения Теперь нетрудно заметить, что при уравнение (10) не имеет решения, т. к.
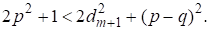
Теорема. Решения диофантова уравнения исчерпываются значениями
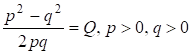
Доказательство. Определим отношение (10)
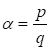
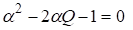
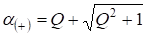
Обозначим, тогда из (10) следует уравнение, имеющее единственное положительное решение (11)
Для случая а) имеем
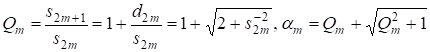
(12)
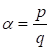
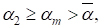
Где четные числа. Из (12) следует, что значения могут принимать только значения монотонно убывающей последовательности. Поэтому причем диапазон возможных значений очень невелик, т. к.
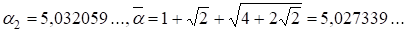
С другой стороны являются решениями уравнения Пелля, т. е. ,что запишем в виде
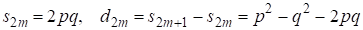
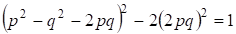
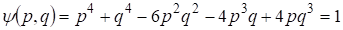
(13)
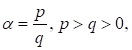
Подобные уравнения хорошо известны в связи с использованием для их решения диофантовых приближений2,стр.359. В данном случае решение упрощается, т. к. рациональные значения должны принадлежать к последовательности (12). При имеем решение (13) , а при рассматриваем (13) в виде
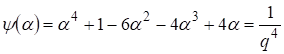
(14)
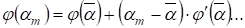
Т. к. то.
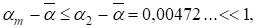
Из (14) имеем оценки
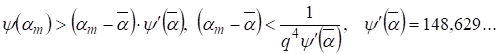
(15)
С другой стороны по теореме о среднем имеем простую оценку Лиувилля 2,стр.359 для рациональных значений
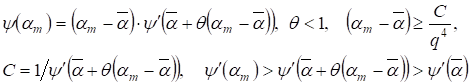
(16)
Из (15) и (16) для рассматриваемой последовательности следует оценка
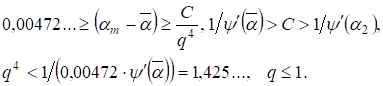
(17)
Окончательно из этого следует, что при уравнения (13) и (14) не имеют решения, т. к. соответствует нечетному, а при в силу оценки Лиувилля.
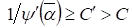
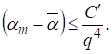
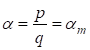
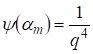
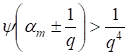
Соотношения (17), по-видимому, требуют пояснения для неспециалистов в области диофантовых уравнений. Из первой строчки (17) следует, что может существовать константа, и тогда для некоторого может существовать оценка Предположим теперь, что это рационально и соответствует решению уравнений (13) и (14). Но тогда будет локальным минимумом, т. к. например, и приходим к противоречию, т. к. в рассматриваемых пределах монотонная функция. Поэтому приходим к выводу, что искомое решение может быть только в начале последовательности, что дает оценку во второй строчке (17).
Для случая б) имеем из (10) и (11)
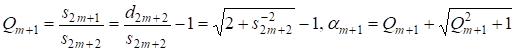
(18)
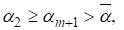
Где четные числа. Из (18) следует, что значения могут принимать только значения из монотонно убывающей последовательности. Поэтому где диапазон возможных значений снова невелик, т. к.
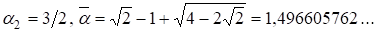
С другой стороны являются решениями уравнения Пелля, т. е. ,что запишем в виде
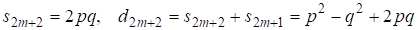
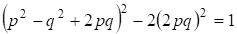
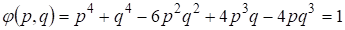
(19)
При имеем решение (19) , и при рассматриваем
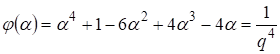
(20)
Рассмотрение, аналогичное проведенному для случая а) приводит к оценке ограничений для возможных значений
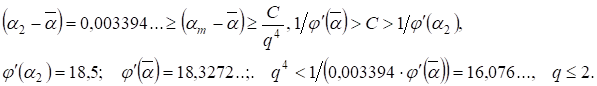
(21)
Из этого следует, что при уравнения (19) и (20) имеют решение, а при, в силу оценки Лиувилля, других решений в рассматриваемой последовательности нет. Теорема доказана.
В заключение следует заметить, что данный подход обобщается применительно к диофантовым уравнениям, приводимым к виду
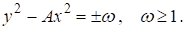
Соответствующие соотношения приведены в Приложении.
Литература
- 1. Эдвардс Г. Последняя Теорема Ферма. Генетическое введение в алгебраическую теорию чисел. М. : Мир, 1980. 2. Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел. М. : Мир, 1987. 3. R. Steyner and N. Tzanakis. Simplifying the Solution of Ljungrens Equation J. Number Theory 37 (1991), 123-132. 4. Chen Jian Hva. Новое решение диофантова уравнения J. Number Theory 48 (1994), 62-74.
Приложение
Решения диофантовых уравнений
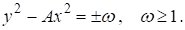
Из известного соотношения для решений уравнения Пелля [2, стр.341]
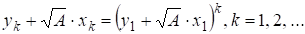
.
следует, что последовательность решений можно представить с помощью алгебраических чисел
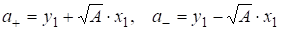
(П1)
С их помощью получаем явные выражения для решений
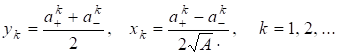
(П2)

Если для данного имеется решение уравнения то имеем рекуррентную цепочку равенств, аналогичную (1)
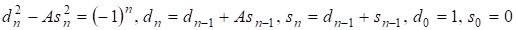
(П3)
В этом случае имеем
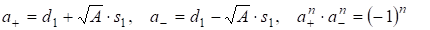
(П4)
Решения (П3) также представляются в виде, аналогичном (П2)
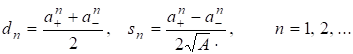
(П5)
Четные значения n дают решения уравнения Пелля, т. е. Нечетные значения n дают решения уравнения
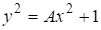
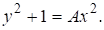
Последовательность решений удобно представить в матричном виде
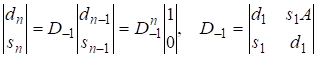
(П6)
Нетрудно проверить, что для уравнения Пелля существуют нелинейные рекуррентные соотношения, обобщающие (4)
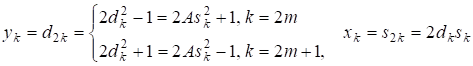
(П7)
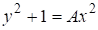
Для аналога нелинейных рекуррентных соотношений уравнения, обобщающих (5), получим
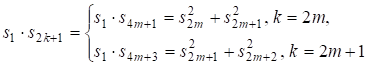
(П8)
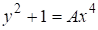
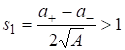
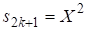
Из этого соотношения обнаруживается интересное следствие для уравнения. Заметим, что из (П5) следует, что делятся на. Поэтому из (П8) нетрудно получить, что Если теперь, то необходимо
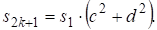
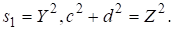
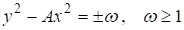
Решения более общего уравнения состоят из конечного числа последовательностей[1, стр.404]
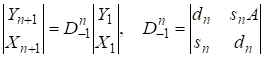
(П9)
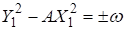
Где ? некоторое начальное (наименьшее) решение уравнения, определяющее последовательность. Тогда из (П9) получим
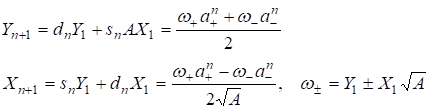
(П10)
Нелинейные рекуррентные соотношения теперь усложняются и должны выводиться и рассматриваться для конкретных значений. Например,
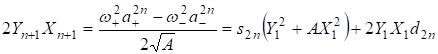
.
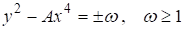
Но при рассмотрении уравнений вида можем, например, получить
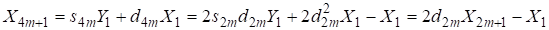
.
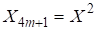
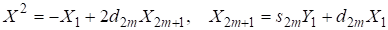
Если теперь в рассматриваемом уравнении, то приходим к соотношениям, которые и являются основой для дальнейшего анализа.
Похожие статьи
-
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах Многие математические...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
Множественная регрессия - уравнение связи с несколькими независимыми переменными: где - зависимая переменная (результативный признак); - независимые...
-
В литературе подобные системы часто называют системами одновременных уравнений, имея в виду, что здесь зависимая переменная одного уравнения может...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта
Исследовать решение обыкновенных дифференциальных уравнений методом Рунге-Кутты. Подробное описание Метод этот пригоден для решения как одиночных...
-
Например, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима...
-
Системы уравнений используемые в экономике - Эконометрика как наука
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных...
-
Заключение - Системы эконометрических уравнений, их применение в эконометрике
В данной курсовой работе я рассмотрела методы восстановления временных зависимостей на основе наименьших квадратов и наименьших модулей. Среди них важное...
-
Пример 1 Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Вопросы: 1. Общее понятие о системах одновременных уравнений. 2. Структурная и приведенная формы модели. 3. Проблема идентификации. 4. Оценивание...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и...
-
Проблема идентифицируемости - Системы эконометрических уравнений, их применение в эконометрике
Идентификация - это единственность соответствия между приведенной и структурной формами модели. При переходе от приведенной формы модели к структурной...
-
1. Название проекта: "Математические модели в экономике". 2. Руководитель: учитель математики Тыкоцкая Л. И. 3. Учебные предметы: математика, экономика....
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
Основные уравнения, движущая сила процесса - Процесс фильтрования
Фильтрование протекает в ламинарной области, что означает небольшой размер пор в слое осадка и фильтровальной перегородке, а также малую скорость...
-
Одна из важнейших задач статистики - определение в рядах динамики общей тенденции развития. Основной тенденцией развития называется плавное и устойчивое...
-
Уравнение Михаэлиса-Ментен и его анализ - Гомогенный и гетерогенный катализ
Уравнемние Михаэмлиса -- Мемнтен -- основное уравнение ферментативной кинетики, описывает зависимость скорости реакции, катализируемой ферментом, от...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...
-
Принятие решений на основе уравнений регрессии - Основы эконометрики
Интерпретация Моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Построение линейного уравнения парной регрессии
Задача Таблица 1 Номер региона Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Среднедневная заработная плата, руб., 1 78 133 2 82...
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
-
По теме "Вариант №2" Определить совместность системы линейных уравнений: Решение: А = RgA = 2. A* = RgA* = 3. Ответ. Система не совместима. 2. Вычислить...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Системы эконометрических уравнений - Основы эконометрики
При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно...
Уравнение Пелля и диофантовые уравнения