Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах
Многие математические модели, применяемые при исследовании процессов, в таких важных областях как математическая биоэкология, механика, автоматизированные системы управления, теория климатических моделей, иммунология и т. д. базируются на дифференциальных уравнениях с отклоняющимся аргументом (например, [1-6]). Широкие возможности применения уравнений с отклоняющимся аргументом в качестве математических моделей способствуют росту интереса к исследованию новых задач для уравнений с частными производными [7-10], которые по сравнению с обыкновенными дифференциальными уравнениями описывают процессы еще в большей степени приближенные к процессам, протекающим на практике [11, 12].
В настоящей работе, методом разделения переменных, установлена разрешимость классической краевой задачи для уравнения в частных производных с инволютивным отклонением аргумента в прямоугольной области.
Уравнение модельный производный
Постановка задачи
Пусть ? односвязная область евклидовой плоскости точек.
В области рассмотрим уравнение
, (1)
Где - достаточно гладкая, причем.
Для уравнения (1) исследована следующая
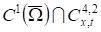
Задача 1. Найти регулярное в области решение уравнения (1) из класса, удовлетворяющее условиям
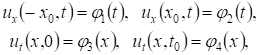
(2)
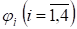
Где - заданные, достаточно гладкие функций.
Доказательство существования и единственности задачи
Для задачи 1 справедлива следующая
Теорема 1. Пусть
1) , ,
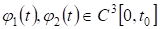
Где, , ;
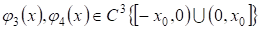
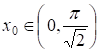
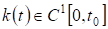
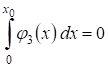
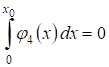
2) , ,
Тогда задача (1), (2) разрешима в требуемом классе функций.
Действительно, разобьем задачу (1), (2) в области на две вспомогательные:
, (3)
, , (4)
, , (5)
, (6)
, , (7)
, , (8)
Где.
Решение уравнения (3) удовлетворяющее однородным граничным условиям (4) будем искать в виде [13]:
. (9)
Подставляя (9) в (3) и опуская нижние индексы, получим
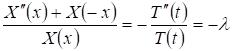
,
Где.
Отсюда, с учетом (4) будем иметь
, (10)
, (11)
. (12)
Исследуем задачу о собственных значениях (10), (11).
Дважды дифференцируя (10), приходим к соотношению:
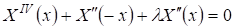
. (13)
С другой стороны из (10) имеем:
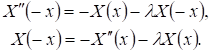
(14)
На основании (13) и принимая во внимание (14), получим
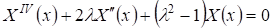
. (15)
Характеристическое уравнение соответствующее (15), будет иметь вид:
.
Разрешая биквадратное уравнение, находим:
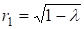
, ,
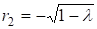
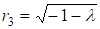
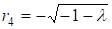
, .
Таким образом, общее решение уравнения (15) может быть записано в виде:
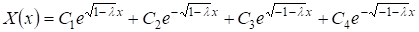
. (16)
Следуя [14, 15], получим из (16) представления решения (10) для различных.
Случай 1: . В этом случае общее решение (10) имеет вид:
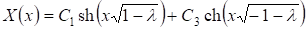
.
Используя условия (11), получим
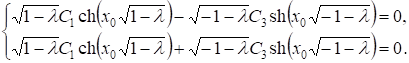
Определитель этой системы
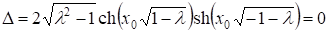
Только при, что противоречит рассматриваемому случаю.
Следовательно, . Откуда заключаем, что.
Случай 2: . При таком значении решение (10) имеет вид:
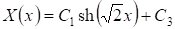
.
Удовлетворяя (11), имеем
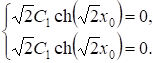
Откуда заключаем, что и.
Этому собственному значению соответствует
, (17)
Где - решение уравнения (12).
Требуя выполнения граничных условий (5) , получаем систему для определения постоянных входящих в (17):
,
.
Таким образом, решение задачи (3)-(5) при определяется соотношением (17).
Случай 3: Для, удовлетворяя общее решение (10)
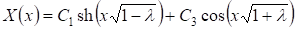
Условиям (11), находим
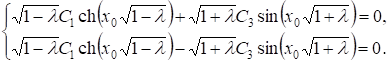
Определитель системы
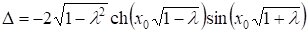
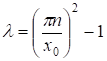
Обращается в нуль либо при, либо при. Следовательно, и, т. к. .
Случай 4: . При указанном значении для всех (10) принимает вид
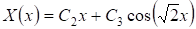
. (18)
Удовлетворяя (18) граничным условиям (11) получим
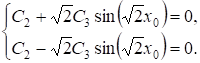
В силу того, что
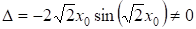
,
Имеем и.
Случай 5. При общее решение (10) принимает вид:
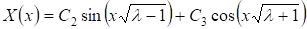
.
Удовлетворяя полученное выражение для граничным условиям (11), будем иметь:
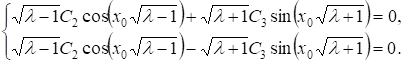
Равенство
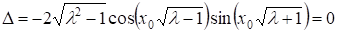
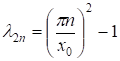
Справедливо при, либо при.
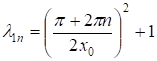
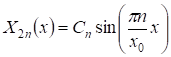
Таким образом, задача (10), (11) имеет собственные значения, и соответствующие им собственные функции, , , где - произвольные постоянные, нуждающиеся в определении.
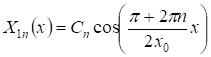
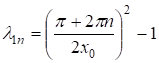
Собственным значениям соответствуют решения уравнения (12) равные
.
Возвращаясь к решению задачи (3)-(5), видим, что функция
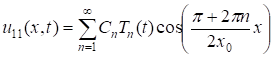
, (19)
Является решением уравнения (3) при
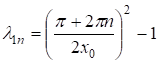
.
Условия (5) позволяют определить значение постоянных входящих в (19).
С учетом условия 1) теоремы 1, функции и, разлагаются в ряд Фурье, который содержит только косинусы, а именно:
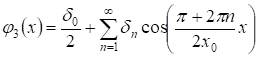
,
,
, ,
,
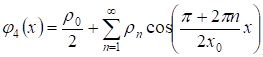
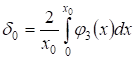
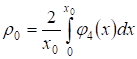
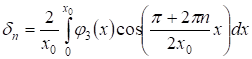
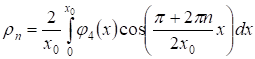
,
Причем ряды и сходятся. Учитывая граничные условия (5), получаем:
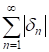
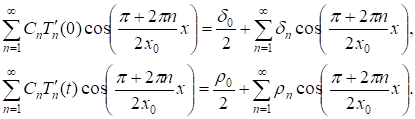
(20)
Сопоставляя соответствующие коэффициенты в полученных соотношениях, а так же учитывая условие 2) теоремы 1 определяем постоянные входящие в (19). Следовательно, ряд (19) с коэффициентами определяемыми по формулам (20), удовлетворяет всем условиям задачи (3)-(5). Переходя к рассмотрению случая собственных значений будем иметь
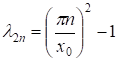
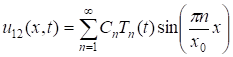
. (21)
Используя условия (5) позволяют определим значение постоянных входящих в (21).
С учетом условия 1) теоремы 1, функции и, разлагаются в ряд Фурье, который содержит только синусы, а именно:
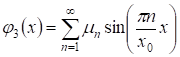
, ,
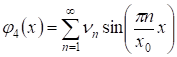
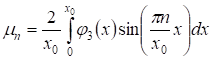
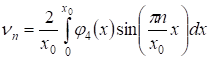
, ,
А ряды и сходятся.
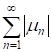
Учитывая граничные условия (5), получаем:
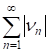
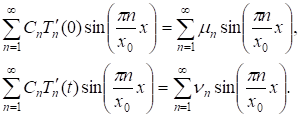
(22)
Сравнивая соответствующие коэффициенты в полученных соотношениях, а так же учитывая условие 2) теоремы 1 определяем постоянные входящие в (21). Представленные выше рассуждения остаются справедливыми и для случая задачи (6)-(8). Причем функция аналогично функции для различных собственных значении находится в виде сходящихся тригонометрических рядов. Таким образом, решение задачи 1 определяется из соотношения.
Заключение
На основе метода разделения переменных было доказано существование решения второй краевой задачи для модельного уравнения в частных производных с инволютивным отклонением в младших членах. Несмотря на то, что результаты работы носят теоретический характер, они могут иметь широкое применение, как и в дальнейших исследованиях уравнений с отклоняющимся аргументом, так и в прикладных задачах.
Список литературы
- 1. Wu J. Theory and Applications of Partial Functional Differential Equations, Springer-Verlag, New York, 1996. 2. Wu J. Traveling wave fronts of reaction-diffusion systems with delay/ J. Wu, X. Zou // J. Dynamics and Differential Equations, 2001. - Vol. 13, No. 3. - P. 651-687. 3. Huang J. Traveling wave fronts in diffusive and cooperative Lotka-Volterra system with delays / J. Huang, X. Zou // J. Math. Anal. Appl, 2002. - Vol. 271. - P. 455-466. 4. Faria T. Nonmonotone travelling waves in a single species reaction-diffusion equation with delay / T. Faria, S. Trofimchuk // J. Differential Equations, 2006. - Vol. 228. - P. 357-376. 5. Trofimchuk E. Slowly oscillating wave solutions of a single species reaction-diffusion equation with delay / E. Trofimchuk, V. Tkachenko, S. Trofimchuk // J. Differential Equations, 2008. - Vol. 245. - P. 2307-2332. 6. Meleshko S. V. On the complete group classification of the reaction-diffusion equation with a delay / S. V. Meleshko, S. Moyo // J. Math. Anal. Appl., 2008. - Vol. 338. - P. 448-466. 7. Hernandez E. A note on partial functional differential equations with state-dependent delay / E. Hernandez, A. Prokopczyk, L. Ladeira // Nonlinear Analysis, R. W.A., 2006. - No. 4. - P. 510-519. 8. Rezounenko A. V. Stability of positive solutions of local partial differential equations with a nonlinear integral delay term / A. V. Rezounenko // Electronic Journal of Qualitative Theory of Differential Equations. Proc. 8th Coll. QTDE, 2008. - No. 17. - P. 1-7. 9. Bzheumikhova O. I. Application of Fourier method to investigation of the Dirichlet problem for partial differential equations with deviating arguments / O. I. Bzheumikhova, V. N. Lesev // International Journal of Differential Equations and Applications, 2013. - Vol. 12, No. 2. - P. 103-120. 10. Лесев В. Н. Об однозначной разрешимости задачи Неймана для эллиптического уравнения с отклоняющимся аргументом / В. Н. Лесев, О. И. Бжеумихова // Экологический вестник научных центров ЧЭС, 2012. - №3. - С. 41-46. 11. Wang L. Global exponential robust stability of reaction-diffusion interval neural networks with time-varying delays / L. Wang, Y. Gao // Physics Letters A, 2006. - Vol. 350. - P. 342-348. 12. Lu J. G. Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions / J. G. Lu. // Chaos, Solitons and Fractals, 2008. - Vol. 35. - P. 116-125. 13. Тихонов А. Н., Самарский А. А. Уравнения математической физики. - М.: Изд-во Наука, 1977. - 735 с. 14. Лесев В. Н. Применение метода Фурье к исследованию задачи Дирихле для уравнения с отклоняющимся аргументом и оператором Лапласа в главной части / В. Н. Лесев, О. И. Бжеумихова // Научный журнал КубГАУ [Электронный ресурс]. - Краснодар: КубГАУ, 2012. - №07(81). - С. 1-10. 15. Бжеумихова О. И. Краевые задачи для модельных уравнений смешанного типа второго порядка с отклоняющимся аргументом / О. И. Бжеумихова, В. Н. Лесев // Обозрение прикладной и промышленной математики, 2011. - Т. 18, вып. 5. - С. 744-745.
Похожие статьи
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта
Исследовать решение обыкновенных дифференциальных уравнений методом Рунге-Кутты. Подробное описание Метод этот пригоден для решения как одиночных...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Уравнение Пелля и диофантовые уравнения
С помощью алгебраических чисел получены явные выражения и нелинейные рекуррентные соотношения для решений диофантовых уравнений, что позволило найти...
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
1. Название проекта: "Математические модели в экономике". 2. Руководитель: учитель математики Тыкоцкая Л. И. 3. Учебные предметы: математика, экономика....
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
Основные задачи анализа временных рядов - Динамические ряды
Принципиальные отличия временного ряда от последовательности наблюдений, образующих случайную выборку, заключаются в следующем: Во-первых, в отличие от...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Табличное представление цен действий и состояний задачи имеет естественные ограничения по масштабируемости задачи на большую размерность. В дискретных...
-
Дифференциальные уравнения - Неопределенный интеграл
Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Частные производные высших порядков - Методы решения системы линейных уравнений
Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Руководитель проекта сообщает тему и цель проекта, знакомит с исполнителями проекта. Акцентирует внимание учащихся на том, что проект носит обучающий...
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах