Линейные уравнения


По теме "Вариант №2"

Определить совместность системы линейных уравнений:

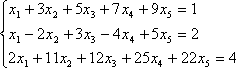
Решение:

А =

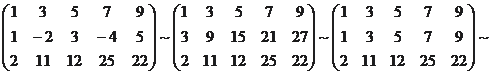
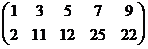
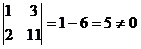
RgA = 2.

A* =

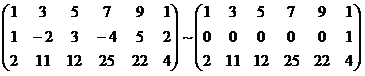
RgA* = 3.

Ответ. Система не совместима.

2. Вычислить ранг матрицы.

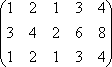
Решение:

От 2; 3 строк отнимаем 1 строку, умноженную соответственно на 3; 1

    1 2 1 3 4 0 -2 -1 -3-4 0 0 0 0 0

1) 2-ую строку делим на -2:

    1 2 1 3 4 0 1 0.5 1.5 2 0 0 0 0 0

2) от 1 строки отнимаем 2 строку, умноженную соответственно на 2:

1 0 0 0 0

0 1 0.5 1.5 2

0 0 0 0 0

Ответ. Так как ненулевых строк 2, то rang(A) = 2.

3. Вычислить определитель:

Решение:

Для вычисления определителя приведем матрицу к треугольному виду.

После этого определитель будет равен произведению элементов главной диагонали.

1) Вычтем из строки 2 строку 1 умноженную на (a2,1/a1,1)= -2

Вычитаемая строка:

-8 -6 -4 -12

Модифицированная матрица:

4 3 2 6

0 11 5 10

3 4 2 3

4 -2 -1 1

2) Вычтем из строки 3 строку 1 умноженную на (a3,1/a1,1) = 3 4

Вычитаемая строка:

3 9 3 9

4 2 2

Модифицированная матрица:

    4 3 2 6 0 11 5 10 0 7 1 -3

4 2 2

4 -2 -1 1

3) Вычтем из строки 4 строку 1 умноженную на (a4,1/a1,1) = 1

Вычитаемая строка:

4 3 2 6

Модифицированная матрица:

    4 3 2 6 0 11 5 10 0 7 1 -3

4 2 2

0 -5 -3 5

4) Вычтем из строки 3 строку 2 умноженную на (a3,2/a2,2) = 7 44

Вычитаемая строка:

0 7 35 35

4 44 22

Модифицированная матрица:

4 3 2 6

0 11 5 10

0 0 -13 -34

44 11

0 -5 -3 5

5) Вычтем из строки 4 строку 2 умноженную на (a4,2/a2,2) = -5 11

Вычитаемая строка:

0 -5 -25 -50

11 11

Модифицированная матрица:

4 3 2 6

0 11 5 10

0 0 -13 -34

44 11

0 0 -8 -5

11 11

6) Вычтем из строки 4 строку 3 умноженную на (a4,3/a3,3) = 32 13

Вычитаемая строка:

0 0 -8 -1088

11 143

Модифицированная матрица:

4 3 2 6

0 11 5 10

0 0 -13 -34

44 11

0 0 0 93

13

7) Вычисляем определитель:

Det[a] = 4 * 11 * -13 * 93 = -93

44 13

Ответ. Определитель равен -93.

4. Найти фундаментальную систему решений системы уравнений:

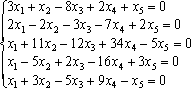
Решение:

1) Найдем ранг матрицы А:

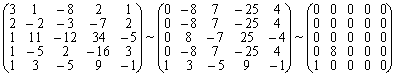
Rang(A)=2.

    2) Оставляем в системе последние два уравнения и переносим слагаемые со свободными неизвестными в правую часть системы: 3) Находим общее решение:

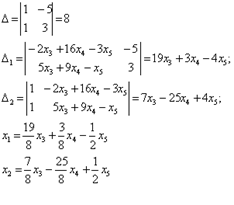
Чтобы найти фундаментальную систему решений, нужно выбрать произвольный отличный от нуля определитель.

Представим его в простейшем виде:

Уравнение решение ранг

    4) Берем строки этого определителя как значения свободных неизвестных, получим 3 решения, которые образовывают фундаментальную систему решений: 5. Решить с помощью теоремы Кронекера-Капелли систему уравнений:

Решение:

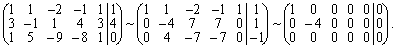
Из последнего преобразования вытекает, что

Начальная система эквивалентна системе:

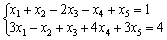
Среди миноров второго порядка, составленных из элементов матрицы коэффициентов при неизвестных, существует хотя бы один отличный от нуля. В нашем случае их несколько. Если отличный от нуля минор выберем из коэффициентов при двух неизвестных, то таким образом мы переведем эти неизвестные в разряд основных. Пусть, например, это неизвестные х1, х2.

Тогда, перенеся остальные неизвестные в правую часть системы уравнений, получим:

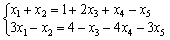
Главный определитель этой системы:

.

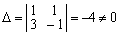
Найдем

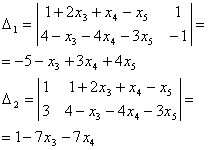
По правилу Крамера:

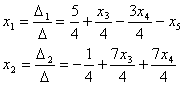
Последние равенства определяют общее решение системы уравнений. Чтобы получить частные решения, достаточно предоставить свободным неизвестным х3, х4, х5 некоторых числовых значений.

Например, если:

Х3 = 0

Х4 = 0

Х5 = 0

Имеем решение:

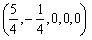
Если:

Х3 = 2

Х4 = 1

Х5 = -2

Решение (3, 5, 2, 1, -2) и т. д.

Таких частных решений в данном случае можно построить бесконечное количество.

6. Построить матрицу, обратную к матрице

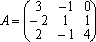
Припишем справа к исходной матрице единичную. В полученной расширенной матрице, левая часть есть исходная матрица, а правая единичная. Затем, производя элементарные операции над строками расширенной матрицы, будем приводить левую часть расширенной матрицы к единичной. По достижению указанной цели правая часть расширенной матрицы будет содержать матрицу обратную к исходной.

1) Сформируем расширенную матрицу:

3

-1

1

0

0

-2

1

1

0

1

0

2

-1

4

0

0

1

2. Разделим строку 1 на:

A1,1 = 3

Получим матрицу:

1
    -1 3

0
    1 3

0

0

-2

1

1

0

1

0

2

-1

4

0

0

1

3) Вычтем из строки 2 строку 1 умноженную на a2,1

Вычитаемая строка:

    -2 2 3 0 -2 3 0 0

Модифицированная матрица:

1
    -1 3

0
    1 3

0

0

0
    1 3

1
    2 3

1

0

2

-1

4

0

0

1

4) Вычтем из строки 3 строку 1 умноженную на

A3,1 = 2

Вычитаемая строка:

2

    -2 3

0

    2 3

0

0

Модифицированная матрица:

1
    ?1 3

0
    1 3

0

0

0
    1 3

1
    2 3

1

0

0
    ?1 3

4

?2

3

0

1

5) Разделим строку 2 на a2,2

Получим матрицу:

1
    -1 3

0
    1 3

0

0

0

1

3

2

3

0

0
    -1 3

4
    -2 3

0

1

6) Вычтем из строки 3 строку 2 умноженную на a3,2

-1

3

Вычитаемая строка:

0
    -1 3

-1
    -2 3

-1

0

Модифицированная матрица:

1
    -1 3

0
    1 3

0

0

0

1

3

2

3

0

0

0

5

0

1

1

Получим матрицу:

1
    -1 3

0
    1 3

0

0

0

1

3

2

3

0

0

0

1

0
    1 5
    1 5

Вычтем из строки 2 строку 3 умноженную на:

A2,3=3

Вычитаемая строка:

0

0

3

0
    3 5
    3 5

Модифицированная матрица:

1
    -1 3

0
    1 3

0

0

0

1

0

2
    12 5
    -3 5

0

0

1

0
    1 5
    1 5

9) Вычтем из строки 1 строку 2 умноженную на a1,2

Вычитаемая строка:

0

    -1 3

0

    -2 3

-4

5

    1 5

Модифицированная матрица:

-1

3

1

0

0

1
    4 5
    -1 5

0

1

0

2
    12 5
    -3 5

0

0

1

0
    1 5
    1 5

В последней расширенной матрице, левая часть есть единичная матрица, а правая обратная к исходной.

Ответ:

1
    4 5
    -1 5

2
    12 5
    -3 5

0
    1 5
    1 5

[A] -1

Похожие статьи




Линейные уравнения

Предыдущая | Следующая