Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта
Исследовать решение обыкновенных дифференциальных уравнений методом Рунге-Кутты.
Подробное описание
Метод этот пригоден для решения как одиночных дифференциальных уравнений первого порядка, так и систем уравнений первого порядка.
Пусть есть уравнение вида
Y'=f (x, y)
С начальным условием
Y(x0)=y0
Предполагается, что отрезок [A, b], на котором будет находиться решение этого уравнения, разбит на N равных частей системой точек (сеткой).
XI=x0+ih (i=0,1.....n), x0=a, xN=b,
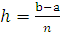
На этой сетке следует найти "развитие" процесса Y(x), т. е. решить так называемую задачу Коши.
Применить этот метод для следующей задачи:
Тело с начальной массой M движется под действием постоянной силы F, При этом масса тела уменьшается со скоростью M'. Сопротивление воздуха пропорционально скорости тела, коэффициент пропорциональности K задан. Соответствующее дифференциальное уравнение, описывающее скорость перемещения тела V(t) Имеет вид:
Метод решения
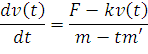
Обозначим через YI приближенное значение искомого решения в точке XI. По методу Рунге-Кутты вычисление приближенного значения YI+1 В следующей точке XI+1=xI+h производится по формулам
YI+1=yI+?YI,
?YI,=(K1I+ K2I +K3I + K4I)
Где
K1I =hf(xI, yI),
K2I = hf(xI+h/2, yI+ K1I/2),
K3I= hf(xI+h/2, yI+ K2I/2)
K4I= hf(xI+h/2, yI+ K3I/2)
Задача:
Фактически решение этой задачи приближенно описывает движение ракеты, расходующей в полете топливо.
Допустим, что V(0)=0.
Тогда уравнение
Имеет следующее аналитическое решение:
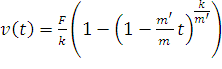
.
Численное решение этого уравнения вычисляется и сравнивается со значениями, полученными в результате работы программы.
Похожие статьи
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Модель Лефевра-Николиса описывает колебательные процессы в следующей цепочке химических реакций: Предполагается, что концентрации веществ A, B, D, E...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах Многие математические...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Метод конечных разностей -- широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на...
-
Метод множителей Лагранжа - Экономико-математические методы
Среди задач (4.1)-(4.3) особое место занимают задачи типа (6.10) , (6.11) Для решения которых можно воспользоваться классическим методом оптимизации...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Модель "вход - выход" для нестационарной системы управления можно представить в следующем виде [2] . Где коэффициенты матриц возмущения и ограничены...
-
В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не...
-
Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системе нечеткого вывода Сугено. Вывод осуществляется за два...
-
Из перечисленного обзора типов ММ, составляющих предмет ИСО, можно выделить следующие особенности ММ ИСО [3]. - Системный подход, заставляющий...
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Знаменитая теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ (по первым буквам фамилий ученых), основана на...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
Одна из важнейших задач статистики - определение в рядах динамики общей тенденции развития. Основной тенденцией развития называется плавное и устойчивое...
-
1. Цыпкин, Я. З. Частотные критерии робастной модальной линейных дискретных систем / Я. З. Цыпкин, Б. Т. Поляк // Автоматика.-1990. - № 5. - С.4-11. 2....
-
Адсорбционные методы исследования свойств поверхности позволяют количественно охарактеризовать происходящие при адсорбции межмолекулярные взаимодействия,...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Для трехотраслевой экономической системы заданы матрица коэффициентов Прямых материальных затрат И вектор конечной продукции Найти коэффициенты полных...
-
Изложение в этой статье посвящено в основном научной области "Математические и инструментальные методы экономики", включающей...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...
-
Метод конечных элементов - МАтематическое моделирование в экономике
- Метод конечных элементов: триангуляция - Метод конечных элементов ( МКЭ ) -- численный метод решения задач прикладной механики. - Широко используется...
-
Заключение - Системы эконометрических уравнений, их применение в эконометрике
В данной курсовой работе я рассмотрела методы восстановления временных зависимостей на основе наименьших квадратов и наименьших модулей. Среди них важное...
Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта