Некоторые векторные равенства


Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

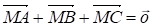
(I)

Где М - центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

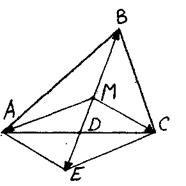
Пусть М - центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ Пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ - параллелограмм. Поэтому . Откуда. Так как, то. Ч. т.д.

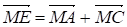
Задача. Доказать, что если М - центроид треугольника АВС и О - произвольная точка пространства, то выполняется равенство

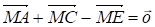
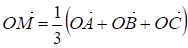
(1)

Доказательство:

Запишем следующие векторные равенства:

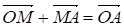
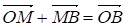
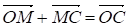
Сложив эти равенства по частям, получаем:

,

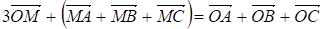
Откуда

Векторный равенство математический

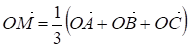
Доказанное равенство также следует отнести к основным векторным соотношениям, так как оно часто используется в решении многих задач.

Основное соотношения. В треугольнике АВС на стороне АС взята точка D так, что АD: DС = M: N.

Тогда имеет месть следующее соотношение:

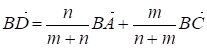
(II)

Доказательство:

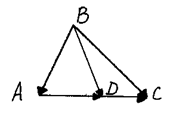
Из треугольника АВС имеем:

.

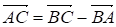
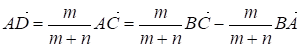
Ч. т.д.

Задача. Через середину Е медианы СС1 треугольника АВС проведена прямая АЕ, пересекающая сторону ВС в точке F. Вычислить АЕ: ЕF и СF: FВ.

Решение

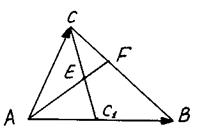
Введем векторы и . Пусть СF: FВ = M: N. Тогда по формуле (II) имеем:

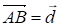
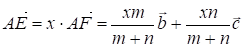
И (1)

Где 0 < Х < 1.

С другой стороны, учитывая, что Е - середина медианы СС1 получаем для АЕ следующее выражение:

(2)

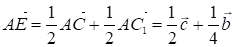
В силу единственности разложения вектора по двум векторам из (1) и (2) получаем систему:

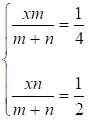
(3)

Разделив по частям первое уравнение системы (3) на второе, получаем, что M: N = 1: 2, т. е. СF: FВ = 1: 2.

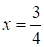
Сложив по частям уравнение системы (3), находим, что , т. е. AE: EF = 3: 4

Основное соотношение. Если точки М и N делят отрезки АВ и CD соответственно в равных отношениях так, что AM: MB = CN: ND = M: N, то выполняется равенство.

(III)

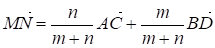
Доказательство:

Для доказательства равенства (III) мы воспользуемся формулой (II). Запишем, что отрезки АВ и CD могут произвольно располагаться относительно друг друга (например, они могут лежать на скрещивающихся прямых и на прямых, принадлежащих одной плоскости).

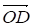
Пусть О - произвольная точка, не принадлежащая ни отрезку АВ, ни отрезку CD. Соединим точку О с точками А, М, В, С, N и D и раcсмотрим векторы и .

Имеем:

,

,

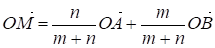
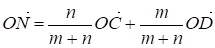
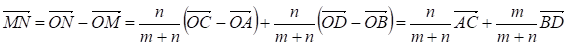
Ч. т. д.

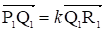
Задача. На прямой M даны три точки Р, Q, R, а на прямой M1 - три точки P1, Q1, R1 причем, . Доказать, что середины отрезков PP1, QQ1 и RR1 Принадлежат одной прямой.

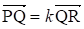
Решение

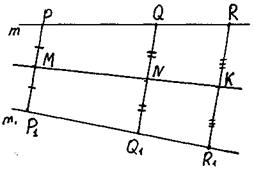
Пусть М, N и К - середины отрезков РР1 QQ1 и RR1 соответственно.

На основании (III) запишем следующие векторные равенства:

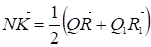
(1)

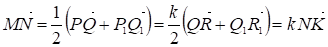
(2)

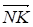
Из (1) и (2) следует, что векторы и коллинеарные. А так как начало одного из них является концом другого, то точки М, N и К принадлежат одной прямой.

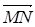
IV Основное соотношение. Дан тетраэдр ABCD и в плоскости его грани ABC Точка М. Доказать, что для разложения

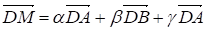
Выполняется равенство

Доказательство:

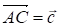
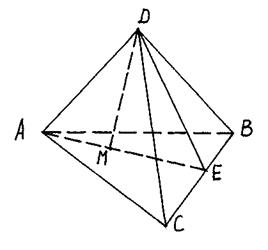
Допустим, что точка М лежит внутри треугольника ABC. Проведем через точки А и М прямую, которая пересекает сторону ВС в точке Е. Пусть Е делит сторону ВС в отношении M: N, т. е.

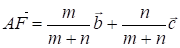
BE: EC = M: N.

Тогда по формуле (II)

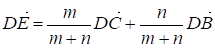
Пусть далее точка М делит отрезок АЕ в отношении P: Q, т. е. AM: ME = P:Q. Тогда

.

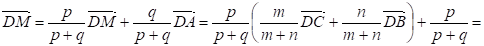
Откуда

Ч. т. д.

Похожие статьи




Некоторые векторные равенства

Предыдущая | Следующая