Введение, Оптимальный метод диагностики основан на непараметрических оценках плотности - Базовые результаты математической теории классификации
Методы классификации - неотъемлемая часть математических методов исследования, интересная теоретически и важная практически. Обзоры этой научной области даны в [1 - 3]. Многие математические методы классификации относятся к непараметрической статистике [4] и к нечисловой статистике [5], т. е. являются неотъемлемой составной частью основного потока современных научных исследований, порожденных новой парадигмой прикладной статистики [6].
В многообразии результатов математической теории классификации выделим три - оптимальный метод диагностики (дискриминантного анализа), адекватный показатель качества алгоритма дискриминантного анализа, доказательство сходимости итерационных алгоритмов кластер-анализа. По нашей оценке, эти результаты являются основными в теории классификации, с ними должен быть знаком каждый специалист, развивающий эту теорию или применяющий ее результаты.
Оптимальный метод диагностики основан на непараметрических оценках плотности
Рассмотрим задачу диагностики с двумя классами. Решение принимают по основе значения x - элемента некоторого пространства. Элементы первого класса имеют плотность f(x), элементы второго - плотность g(x). Поступает на рассмотрение новый объект со значением Х. К какому классу его отнести?
Задачу диагностики можно переформулировать в терминах теории проверки статистических гипотез. Пусть согласно нулевой гипотезе H0 результат наблюдения Х имеет распределение с плотностью f(x), а согласно альтернативной гипотезе H1 результат наблюдения Х имеет распределение с плотностью g(x). Отнесение Х к первому классу соответствует принятию гипотезы H0 (и отклонению гипотезы H1), а отнесение Х ко второму классу соответствует принятию гипотезы H1 (и отклонению гипотезы H0).
В теории проверки статистических гипотез выявлена важная роль критерия отношения правдоподобия (см., например, [7]). Статистика этого критерия имеет вид
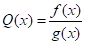
. (1)
Правило принятия решения основано на сравнении с порогом С значения статистики критерия Q(X), рассчитанного для поступившего на рассмотрение нового объекта со значением Х. Таким образом, если Q(X) > C, то Х относят к первому классу, в противном случае - ко второму.
С точки зрения здравого смысла критерий отношения правдоподобия является естественным, как отношение шансов (вероятностей) за то, что новый объект со значением Х относится к первому или ко второму классу соответственно. Важно, что согласно лемме Неймана-Пирсона этот критерий является наиболее мощным критерием среди всех статистических критериев, имеющих один и тот же заданный уровень значимости (понятия "уровень значимости" и "мощность критерия" - базовые в математической статистике). (Строго говоря, под термином "лемма" понимают верное (т. е. доказанное) утверждение, полезное не само по себе, а для доказательства других утверждений. Однако лемма Неймана-Пирсона - основной результат математической статистики, важный сам по себе. Поэтому лемму Неймана-Пирсона часто называют фундаментальной леммой математической статистики.)
Итак, оптимальный метод диагностики существует и задается с помощью статистики Q(X) (см. формулу (1)).
Однако при решении практических задач диагностики плотности f(x) и g(x) обычно неизвестны. В таких случаях строят правило диагностики на основе обучающих выборок. А именно, предполагается, что имеются m объектов из первого класса (обучающая выборка для первого класса) и n объектов из второго класса (обучающая выборка для второго класса). В вероятностно-статистической теории принимают, что обучающую выборку можно моделировать как совокупность независимых одинаково распределенных случайных объектов с соответствующей плотностью. Развиты непараметрические методы состоятельного оценивания неизвестной плотности [8, 9]. Пусть fm(x) и gn(x) - состоятельные оценки плотностей f(x) и g(x) соответственно по обучающим выборкам. Рассмотрим выборочный аналог статистики критерия отношения правдоподобия
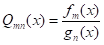
. (2)
Из состоятельности fm(x) и gn(x) вытекает, что Qmn(x) для того же элемента x является состоятельной оценкой Q(х) при безграничном росте объемов обучающих выборок. При справедливости обычно выполненного предположения равномерной сходимости из оптимальности критерия отношения правдоподобия для полностью известных плотностей вытекает асимптотическая оптимальность выборочного аналога этого критерия, основанного на сравнении с порогом С значения статистики (2).
В задачах диагностики со многими классами оптимальное решение также выражается через плотности, соответствующие классам. Например, при постановке задачи в терминах статистических решающих правил [10, 11]. Во всех таких случаях асимптотически оптимальное решение получаем путем замены неизвестных плотностей их состоятельными оценками [8, 9].
Наличие описанных выше оптимальных и асимптотически оптимальных правил диагностики (дискриминантного анализа, распознавания образов с учителем) не означает, что не следует разрабатывать новые алгоритмы диагностики. Исходя, например, из необходимости сокращения машинной памяти и времени на расчеты. Однако, на наш взгляд, необходимо сравнивать новые алгоритмы с известными оптимальными и асимптотически оптимальными алгоритмами по тем или иным показателям качества.
Похожие статьи
-
Часто используют такой показатель качества алгоритма диагностики, как "вероятность (или доля) правильной классификации (диагностики)" [12, 13] - чем этот...
-
Аннотация - Базовые результаты математической теории классификации
Математическая теория классификации содержит большое число подходов, моделей, методов, алгоритмов. Эта теория весьма многообразна. Выделим в ней три...
-
Сначала обсудим один из широко применяемых методов кластер-анализа - с метода k-средних. Он предназначен для разбиения исходного множества элементов...
-
Прогностическая сила - Базовые результаты математической теории классификации
С целью поиска приемлемого показателя качества диагностики рассмотрим восходящую к Р. Фишеру [20] широко известную параметрическую вероятностную модель...
-
Литература - Базовые результаты математической теории классификации
1. Орлов А. И. О развитии математических методов теории классификации // Заводская лаборатория. Диагностика материалов. 2009. Т.75. №7. С.51-63. 2....
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
В 2011 - 2015 гг. в серии статей в научных журналах и докладов на международных, зарубежных и всероссийских научных конференциях была представлена...
-
Планирование и прогнозирование являются одними из важнейших задач любого предприятия. Особенно актуальными эти аспекты делают нестабильность...
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Большое число экономических и планово-производственных задач связано с распределением каких-либо, как правило, ограниченных ресурсов (сырья, рабочей...
-
Сравнение старой и новой парадигм - О новой парадигме математических методов исследования
Проведем развернутое сравнение старой и новой парадигм математических методов исследования. При этом опираемся на материалы раздела "Математические...
-
Введение - Моделирование математической модели теплообменника
Математический динамический модель канал Качественные и количественные изменения в промышленности, науке и технике составляют основу для значительного...
-
Изложение в этой статье посвящено в основном научной области "Математические и инструментальные методы экономики", включающей...
-
Теория оптимального программирования - Оптимальное программирование
Оптимальное программирование [optimal programming] -- применение в экономике методов математического программирования. Часто эти термины определяют как...
-
Введение - Оптимальное программирование
Линейный программирование транспортный задача Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при...
-
Введение - Экономико-математические методы
Экономические проблемы, возникающие перед специалистами, в большинстве своем сложные. Они зависят от множества различных, иногда противоречащих друг...
-
В этом случае лучшим считается вариант, у которого суммарная величина отдельных целевых функций принимает максимальное значение: F Max = = max...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Классификация экономико-математических методов - История развития методов и моделей в экономике
Велика роль математических моделей при описании экономических объектов и процессов, что, безусловно, подтверждается историей развития этого направления...
-
Комментарии к третьему разделу курсовой работы В третьем разделе курсовой работы студенту предлагается определить оптимальную стратегию заказа в условиях...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Статистическая обработка результатов измерений - обработка измерительной информации с целью получения достоверных данных. Разнообразие задач, решаемых с...
-
Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик...
-
Оптимизация, Верификация модели - Синтез скоринговой модели методом системно-когнитивного анализа
Оптимизируем полученную модель с помощью удаления признаков, по которым имеется недостаточно данных. За пороговое значение встреч признаков в модели...
-
Метод множителей Лагранжа - Экономико-математические методы
Среди задач (4.1)-(4.3) особое место занимают задачи типа (6.10) , (6.11) Для решения которых можно воспользоваться классическим методом оптимизации...
-
Математическое моделирование экономических явлений и процессов является, как указывалось выше, важным инструментом экономического анализа. Оно позволяет...
-
Упорядочение и классификация объектов с противоречивыми признаками
Упорядочение и классификация объектов с противоречивыми признаками Мультимножество или множество с повторяющимися элементами служит удобной...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Экономико-математические методы выявления рисков
Применение экономико-математических методов позволяет провести качественный и количественный анализ экономических явлений, дать количественную оценку...
-
Этапы экономико-математического моделирования - Методы экономико-математического моделирования
Основные этапы процесса моделирования уже рассматривались выше. В различных отраслях знаний, в том числе и в экономике, они приобретают свои...
-
К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло,...
-
Итак, в первых двух разделах курсовой работы мы использовали модуль Excel "Поиск решении" для решения задачи общего линейного программирования (1 раздел)...
-
Введение - Модели оптимального плана управления запасами
Экономико-математической теории управления запасами в 2015 г. исполняется 100 лет (отсчитывая с работы Ф. Харриса [1]). Она входит в логистику - одну из...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
Методы исследования математических моделей - Математическое моделирование в менеджменте и маркетинге
Все методы математического моделирования можно разделить на четыре класса: -аналитические (априорные); -имитационные (априорно-апостериорные) модели;...
-
Определим сначала максимальные (оптимальные) нормализованное значения по каждому из трех нормализованных критериев: F(ХI=1) = 1; f(ХI=2) = 1; f(ХI=3) =...
-
Теория алгоритмов. Основные результаты, Программы как данные - Рекурсивные функции
Вместо предисловия . Сверх-идеей любой научной теории можно считать перевод знания из сферы подсознательного, интуитивногов осознанную, точную и...
-
Разработка новой парадигмы - О новой парадигме математических методов исследования
Организационно-экономическое и экономико-математическое моделирование, эконометрика и статистика предоставляют интеллектуальные инструменты для решения...
Введение, Оптимальный метод диагностики основан на непараметрических оценках плотности - Базовые результаты математической теории классификации