Латиноамериканская модель глобального развития - Математическое и компьютерное моделирование в естествознании
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью глобального развития. Предпосылки для выполнения работы при обсуждении модели "Мир-3" послужил тезис о том, что основные преграды на пути гармонического развития человечества заключаещися главным образом в неравномерном распределении богатства между различными странами.
В модели Эрреры за основную цель развития человеческого общества принято достижение удовлетворительных условий жизни всеми странами мира, а не просто рост материального потребления. Под удовлетворительными условиями понимаются некоторые достаточно высокие уровни медицинского обслуживания, образования, обеспеченности питанием и жильем.
Применение компьютеров в научных исследованиях является необходимым условием изучения сложных систем. Традиционная методология взаимосвязи теории и эксперимента должна быть дополнена принципами компьютерного моделирования. Эта новая эффективная процедура дает возможность целостного изучения поведения наиболее сложных систем как естественных, так и создаваемых для проверки теоретических гипотез.
Методами компьютерного моделирования пользуются специалисты практически всех отраслей и областей науки и техники - от истории до космонавтики, поскольку с их помощью можно прогнозировать и даже имитировать явления, события или проектируемые предметы в заранее заданных параметрах.
Компьютерное моделирование в естествознании: возможности, достижения, перспективы
Большинство естественнонаучных теорий очень похожи на математику внутренней логикой своего построения. В основе любой математической теории лежит несколько аксиом, а все частные результаты, называемые теоремами, выводятся из аксиом посредством дедуктивных логических рассуждений. Аксиомы являются идеальными абстрактными образами реальных объектов.
Точно также во всех т. н. точных науках после этапа накопления экспериментальных данных формулируются основные законы, из которых могут быть получены все свойства различных систем и процессов, охватываемых данной теорией. Компактная и точная формулировка законов естествознания делается на языке математики в виде каких-либо уравнений. Таким образом, математической моделью любой реальной системы является некоторое уравнение или система уравнений с определенными значениями параметров и определенными граничными условиями.
Во многих случаях для решения этих уравнений традиционными аналитическими методами требуется использование серьезного, порой, очень громоздкого математического аппарата. Иногда решения в аналитической форме вообще отсутствуют. Попытка ограничиться рассмотрением простейших систем, для которых решение основных уравнений может быть найдено элементарными методами, существенно обедняет наши представления об окружающем мире.
Эффективный путь преодоления этих трудностей - построение компьютерной модели изучаемого явления, под которой понимается совокупность численных методов решения основных уравнений, алгоритмов их реализации и компьютерных программ. Хорошая компьютерная модель превращает компьютер из сверхбыстрого калькулятора в интеллектуальный инструмент, способствующий открытию новых эффектов, явлений и даже созданию новых теорий.
Результативность компьютерной модели в значительной степени определяется качеством используемого программного обеспечения. Основные требования, предъявляемые к программам - это, конечно, простота ввода и корректировки исходных данных, а также визуализация (наглядность) результатов счета. Сегодня имеются и мощные специализированные системы программирования (MAPLE, SolidWorks, AutoCAD и др.) и специальные программы, в которых реализуется удобные графические пользовательские возможности.
Использование компьютерных моделей превращает компьютер в универсальную экспериментальную установку. В компьютерном эксперименте обеспечен полный контроль за всеми параметрами системы, компьютерный эксперимент дешев и безопасен, с помощью компьютера удается ставить "принципиально невозможные" эксперименты (геологические процессы, космология, экологические катастрофы и т. д.).
Приведем примеры естественнонаучных задач, смоделированных при помощи компьютера:
1. Постановка задачи. Проверить в компьютерном эксперименте выполнимость второго закона Кеплера, определяющего движение тел по замкнутой траектории.
В начале работы необходимо уточнить формулировку и условия задачи:
По заданным условиям (начальные координаты малого тела, начальная скорость малого тела, масса большого тела) построить траекторию движения малого тела, проверить является ли она эллипсом, если да, то проверить выполнение второго закона Кеплера для данных тел. Считать, что система, в которой производится моделирование, состоит из 2х тел. Считать гравитационную постоянную. Считать центральное тело неподвижным. Производить расчеты для тел, удаленных от центра системы не более чем на 100 а. е. Считать а. е. = 149 597 890 000м, а центром системы - центр большого тела.
Далее опишем методы исследования процесса:
По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Если поместить начало системы координат на одном из тел (размерами тел по сравнению с расстоянием между ними будем пренебрегать), математическая запись силы, действующей на второе тело, имеет вид (рис. 1)

(1)
Здесь G = 6,67-10-11 м3/кг-с2) - гравитационная постоянная.
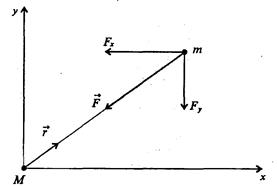
Рис. 1 Выбор системы координат при решении задачи двух тел
Знак "минус" в формуле (1) связан с тем, что гравитационная сила является силой притяжения, т. е. стремится уменьшить расстояние г между телами.
Рассмотрим случай, когда центральным телом является Солнце, масса которого
М=1,9891Ч1030 кг, а обращающимся Земля, т. е. за расстояние примем 1 астрономическую единицу, равную 149 597 890 000м, пренебрегая при этом относительно небольшими силами притяжения от всех прочих небесных тел. Разумеется, мы тем самым произвели ранжирование факторов, и наши последующие действия имеют отношение к реальности лишь в меру соблюдения определенных условий.
Уравнение, описывающее движение тела m в указанной системе координат, имеет вид

Или в проекциях на оси х, у

(2)
Интересующая нас орбита сильно зависит от "начальной скорости" тела т и "начального расстояния. При моделировании нам придется принять некоторое положение условно за начало, а затем изучать движение дальше. Очень часто космические тела движутся практически с постоянной скоростью по орбитам, близким к круговым. Для таких орбит легко найти элементарное соотношение между скоростью и радиусом. В этом случае сила тяготения выступает в роли центростремительной, а центростремительная сила при постоянной скорости выражается известной из начального курса физики формулой mv2/r. Таким образом, имеем

Или

- (3) - искомое соотношение.
Период движения по такой орбите

Если соотношение (3) нарушено, то орбита не будет круговой. Выяснить, какой она будет, можно в ходе численного моделирования. Сведем (2) к системе четырех дифференциальных уравнений первого порядка:

(4).
Методы вычислений. При использовании математической модели движения получена система дифференциальных уравнений (4), описывающая параметры движения тела. Для вычисления траектории движения необходимо решить систему уравнений 4, для ее решения необходимо применять численные методы. Был использован метод Эйлера.
Метод Эйлера дает возможность построить таблично заданную функцию на некотором интервале ее значений. По методу Эйлера напишем систему соотношений (6) для нахождения таблицы значений функций описанных уравнением (3) и удовлетворяющих условию (5). Подробнее процесс построения таблицы значений функций по методу Эйлера описан в [6].

(5)

(6)
Где шаг сетки значений h.
Для проверки закона Кеплера нам необходимо сравнить площади секторов, заметаемых радиус-вектором за одинаковые промежутки времени. Если площади будут равные в достаточной степени точности, то мы сможем утверждать, что второй закон Кеплера выполняется. Для этого возьмем достаточно малое приращение по времени, для того, чтобы площадь данного сектора стремилась к площади треугольника, со сторонами а, b, c (рис.2).

Рис.2
Для вычисления площади треугольника, у которого заданы координаты вершин можно воспользоваться формулой Герона

(7)
Где p - полупериметр треугольника, изображенного на рис. 2, a, b, c - длины его сторон.
Из системы уравнений (7) мы можем выразить координаты точек эллипса, удовлетворяющих заданной степени точности. Координаты начала векторов a, b будут равны (0,0), т. к. за начало координат принято Солнце. Длины векторов вычисляются по известной из алгебры формуле:

(8)
Таким образом, мы сможем вычислить площади треугольников, которые в совокупности будут давать площадь самого эллипса. Для того, чтобы утверждать, что закон Кеплера справедлив, возьмем наибольшую и наименьшую из полученных площадей, если разница между ними будет незначительна (к примеру, равна до пятого знака после запятой), то закон выполняется, так как площадь больших секторов для больших промежутков времени есть сумма полученных секторов и данного приращения по времени, мы можем утверждать, что закон Кеплера будет выполняться при любых условиях, если он будет выполняться при заданных.
После того как модель готова остается только написать программу, которая будет реализовывать данный алгоритм. Наша программа написана на языке С++.
Входные данные программы:
Mg= 132672970000000000000.0 метров - произведение массы Солнца на константу g.
X = 149600000000.0 - начальная координата малого тела по оси х
Y = 0 - начальная координата малого тела по оси у
Vx = 0 м/с - начальная скорость по оси х
Vy = 29785 м/с - начальная скорость по оси у
Выходные данные программы:
SMax - площадь максимального из заметаемых радиус-вектором секторов
SMin - площадь минимального из заметаемых радиус-вектором секторов
Тестирование:
При заданных входных параметрах, площади треугольников, получаемых с помощью описанного выше алгоритма приближенно равны (не равны точно, т. к. в языке С++ переменные типа float при вычислениях округляются). sMax = 8.02207e+018, sMin = 8.01897e+018. Это позволяет говорить о том, что второй закон Кеплера справедлив.
2. Постановка задачи. Построить изолинии поля, созданного четырьмя одноименными зарядами, находящимися в вершинах прямоугольника. Значения зарядов (при последовательном обходе вершин) есть q, 2q, 3q, 4q.
Для того чтобы понять, какой способ условного изображения поля наиболее удобен и понятен было нам было необходимо понять суть самого предмета электродинамики, и на основе полученных знаний, предположить, какими могут быть альтернативные способы. Для этого нами были прочитаны: главы 36-40 [5], глава 3.8 [3], и раздел "Описание физических процессов в приближении сплошной среды" [4], в последствии чего было выявлено, что наиболее эффективным и наглядным способом является изображение поля линиями равного потенциала.


Описание метода исследования процесса. Для построения изолиний поля, созданного несколькими зарядами, можно воспользоваться принципом суперпозиции, то есть потенциал в каждой точке поля равен, где цI Создаются в этой точке i-м зарядом. Потенциал поля, созданного зарядом Q на расстоянии r от него, равен, где Е0 - электрическая постоянная.

Для решения воспользуемся методом сеток. Пусть поле создается системой зарядов Q1 ... QP с координатами соответственно (x1, y1),...,( xP, yP). Выберем по осям х и у и некоторые шаги hX и hY и покроем плоскость сеткой, образованной прямыми, параллельными осям х и у и отстоящими друг от друга на расстояниях hX и hY. Точки пересечения этих прямых - узлы сетки. Пронумеруем их так: начало координат (0, 0), следующий по оси х вправо - (0, 1), влево - (0, -1); по оси у вверх - (1, 0), вниз - (-1, 0) и т. д. Значения потенциала, создаваемого системой зарядов Q1 ... QР в узле (i, k), согласно принципу суперпозиции, таково (i - номер строки, k - столбца сетки): .
Ограничимся прямоугольной областью в плоскости ху: [-mhX, mhX] по оси х и [-nhY, nhY] по оси у. В этой области (2m + l) - (2n + l) узлов. Вычислим значения потенциала в каждом из них по указанным формулам.
Фиксируем некоторое значение потенциала Ф и построим изолинию, соответствующую этому значению. Для этого проходим, к примеру, по i-ой горизонтальной линии сетки и ищем среди ее узлов такие соседние значения потенциала, причем выполняется. Если такая пара узлов найдена, то координату точки, значение потенциала в которой равна Ф, найдем приближенно с помощью линейной интерполяции:

Найдя в данной горизонтали все такие точки, переходим к следующей горизонтали, пока не исчерпаем их все. Для этого надо совершить двойной циклический проход: во внешнем цикле перебирать i от - п до +п, во внутреннем перебирать k от - т до +т.

После этого надо найти нужные точки на вертикальных линиях сетки. Формулы аналогичны и имеют вид: .
После прохождения всех горизонтальных и вертикальных линий сетки находятся все точки на этих линиях, в которых потенциал равен Ф. Проведя через эти точки линии, мы получим изолинию. Затем берем другие значения Ф и, повторяя указанную процедуру, получаем таким образом семейство изолиний.
Итак, предполагая, что все заряды лежат в одной плоскости, и изолинии строятся тоже лишь в этой плоскости, в главе II приступаем к разработке программы на языке Pascal.
Реализация программы: входными параметрами нашей программы являются координаты точек, в которых расположены заряды; величины зарядов; значения потенциалов.
Следовательно выходные и выходные данные будут представлены в следующем виде:
Входные данные:
Массив абсцисс точек, в которых расположены заряды. Обозначим х
Массив ординат точек, в которых расположены заряды. Обозначим у
Массив, который содержит значения зарядов. Обозначим q
Массив, который содержит значения потенциалов. Обозначим g
Выходные данные:
Семейство изолиний.
Далее нам остается лишь корректно реализовать предложенный нами в главе I алгоритм.
Результат работы программы приведен на следующем рисунке:

Конечно, реализованные нами задачи носят скорее учебный характер, чем практический, но и они дают понять, что и серьезные естественнонаучные проблемы можно решать, построив сначала математическую, а потом компьютерную модель. Данный метод может не только наглядно демонстрировать нам те или иные природные явления, но и помогать нам в их прогнозировании или оценке, что, безусловно, несет большой вклад в науку.
Похожие статьи
-
Следующим этапом в работах по глобальному моделированию явился проект "Стратегия выживания", который возглавил М. Месарович (США) и Э. Пестель (ФРГ)....
-
Введение - Математическое и компьютерное моделирование в естествознании
При изучении любого явления вначале получают качественное описание проблемы. На этапе моделирования качественное представление переходит в...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Моделирование водных экосистем - Математическое и компьютерное моделирование в естествознании
Научно-технический прогресс, развитие сельского хозяйства, урбанизация привели к загрязнению природных вод. Проблема загрязнения вод приобрела глобальный...
-
В воздушном зазоре электрических машин всегда, наряду с основной гармонической составляющей вращающегося магнитного поля, присутствуют гармонические...
-
Методы построения решений по математическим моделям - Математическое моделирование в электромеханике
Системы дифференциальных уравнений, полученные для конкретных ти-пов электрических машин, содержат в скрытом виде исчерпывающую инфор-мацию о всех...
-
Введение - Моделирование математической модели теплообменника
Математический динамический модель канал Качественные и количественные изменения в промышленности, науке и технике составляют основу для значительного...
-
Методы математического моделирования экономики развиваются уже почти 200 лет. За это время созданы десятки тысяч моделей разной степени общности и...
-
Первая попытка формализовать описание экологических процессов была принята в 1971 г. американским исследователем Дж. Форрестером. В своей книге "Мировая...
-
В настоящее время проблема "Человек и среда его обитания" широко обсуждается во всем мире. Рост населения, истощение природных ресурсов, отрицательные...
-
Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их...
-
1. Универсальность - характеризует полноту отображения моделью изучаемых свойств реального объекта. 2. Адекватность - способность отражать нужные...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
Выделим случай, когда входной сигнал X ( T ) является элементарной функцией 1( T ). Реакцию системы на воздействие 1( T ) можно компактно: [1] Где...
-
Z -преобразование является одним из математических методов, разработанных для анализа и проектирования дискретных систем. Аппарат Z -преобразования...
-
Любой электромеханический преобразователь можно рассматривать в установившемся и динамическом режиме. Модель в установившемся режиме, по сути, является...
-
Необходимо составить математическое описание теплообменника, в котором жидкий продукт нагревается насыщенным водяным паром (расход, кг/с), до температуры...
-
Методы исследования математических моделей - Математическое моделирование в менеджменте и маркетинге
Все методы математического моделирования можно разделить на четыре класса: -аналитические (априорные); -имитационные (априорно-апостериорные) модели;...
-
Как в теоретическом, так и в прикладном отношении представляют интерес работы по построению и использованию производственных функций для анализа...
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
Структурная и приведенная формы модели. - Моделирование в эконометрике
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные Переменные...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Классификация экономико-математических методов - История развития методов и моделей в экономике
Велика роль математических моделей при описании экономических объектов и процессов, что, безусловно, подтверждается историей развития этого направления...
-
Классификация экономико-математических моделей. - Моделирование перспективного развития экономики
Математические модели экономических процессов и явлений более кратко можно назвать экономико-математическими моделями. Для классификации этих моделей...
-
Понятие многосекторной экономики Многосекторная экономика-- экономическая система, в которой на рыночной основе сосуществуют частная, государственная и...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
Важнейшие математические модели обычно обладают важным свойством Универсальности : принципиально разные реальные явления могут описываться одной и той же...
-
Заключение, Список использованной литературы - Моделирование математической модели теплообменника
В данной курсовой работе была получена математическая модель теплообменника в виде дифференциальных уравнений. Также была получена передаточная функция...
-
Модель Мальтуса Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением Где б -- некоторый параметр,...
-
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была "по-винна" математика, развивающаяся...
-
Как и каждый достаточно ярко выраженный класс экономико-математических моделей, совокупность моделей календарного планирования обладает рядом...
-
Математическое моделирование экономических явлений и процессов с целью оптимизации процессов управления - область научно-практической деятельности,...
-
В инженерной практике в настоящее время широко используются современные программные комплексы позволяющие моделировать сложные физические процессы. Для...
-
Моделирование рынка тепла - Расчетная модель оптимизации системы теплоснабжения региона
Энергосистема теплоснабжение конкуренция регион В нашей предыдущей работе [1] была разработана методология анализа конкуренции ТЭЦ и/или котельных, а...
-
Примеры лаговых моделей в экономике - Экономическое моделирование временных рядов
Модель адаптивных ожиданий Моделью адаптивных ожиданий называется динамическая эконометрическая модель, которая учитывает предполагаемое (или желаемое)...
-
Моделирование временной переменная автокорреляция Главным инструментом эконометрического исследования является модель. Выделяют три основных класса...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
-
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение...
-
Построение, или моделирование, конечной факторной системы для анализируемого экономического показателя хозяйственной деятельности можно осуществить как...
Латиноамериканская модель глобального развития - Математическое и компьютерное моделирование в естествознании