Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о нормальном распределении шумов в модели дает оценку параметров, совпадающую с оценкой максимального правдоподобия. К недостаткам этого метода можно отнести высокую чувствительность к выбросам в данных: даже одно наблюдение с нетипичными значениями может сильно повлиять на оценки параметров и изменить общую картину. В сравнении с методом наименьших квадратов, метод наименьших модулей в меньшей степени подвержен влиянию выбросов в данных, в случае распределения ошибок согласно закону Лапласа (двойному экспоненциальному) он дает оценку, обеспечивающую максимум функции правдоподобия.
Ранговый метод оценки параметров линейной регрессии является альтернативой двум вышеупомянутым методам. Предполагается, что он является более устойчивым к выбросам в данных и обеспечивает более точную оценку параметров регрессионной модели в случае, когда распределение шумов в модели имеет "тяжелые хвосты" (например, распределение Коши), чем МНК, и лучше, чем МНМ, оценивает значения параметров в моделях с шумами, имеющими "двугорбое" распределение. В этой части будет рассмотрен метод построения ранговой оценки параметров линейной регрессионной модели.
Итак, рассмотрим линейную модель:
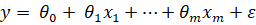
,
Где y - наблюдаемое значение зависимой переменной,
X1,..., xM - значения независимых объясняющих переменных (или регрессоров),
и0,..., иM - неизвестные параметры модели,
А е - случайная ошибка наблюдения, имеющая нулевое математическое ожидание.
При наличии n наблюдений значения зависимой переменной и набора ее регрессоров, модель запишется в матричном виде:
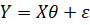
,
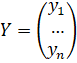
Где - вектор наблюдаемых значений зависимой переменной,
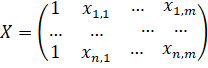
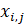
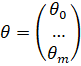
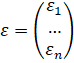
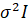
- матрица плана полного столбцового ранга, число столбцов которой не превышает числа строк, ее элемент - значение j-го регрессора в i-м наблюдении, - вектор параметров, а - вектор независимых, одинаково распределенных ошибок с нулевым математическим ожиданием и ковариационной матрицей вида, где I - единичная матрица размера nxn.
Для построения оценки ранговым методом требуется ввести функцию D(Y-Xи) - меру изменчивости. Мерой изменчивости (или функцией потерь) называется такая функция D(.), что
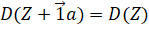
и
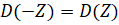
Для любого n-мерного вектора Z и скаляра a. Если рассматривать эту функцию как функцию от m переменных - параметров и1, ... , иM, то точка, в которой функция D достигает минимума, будет являться оценкой параметров регрессионной модели. Функция изменчивости не зависит от сдвига, поэтому оценка свободного члена и0 для модели проводится отдельно от оценки остальных параметров.
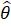
В статье Л. Джекла Louis A. Jaeckel, Estimating Regression Coefficients by Minimizing the Dispersion of the Residuals// The Annals of Mathematical Statistics, Volume 43, № 5 (1972), 1972, c. 1450 ранговой оценкой вектора параметров (без свободного члена и0) называется такой вектор, который минимизирует функцию
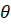
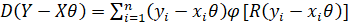
,
Где yI - i-й элемент вектора Y, xI - i-я строка матрицы X (без столбца единиц), R(yI - xIИ) - ранг величины yI - xIИ среди всех величин yK - xKИ при k от 1 до n, а в качестве функции ц берется Т. Хеттманспергер "Статистические выводы, основанные на рангах"/ М.: Финансы и статистика,1987, с. 242
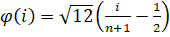
.
В книге Т. Хеттманспергера Т. Хеттманспергер "Статистические выводы, основанные на рангах"/ М.: Финансы и статистика,1987, с. 242 для построения оценок параметров и1, ... , иM регрессионной модели предлагается найти частные производные функции D(Y-Xи) по переменным иI:
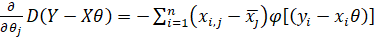
,
И решить систему уравнений:
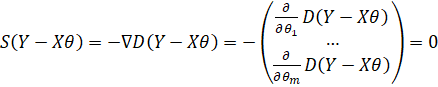
.
Недостатком такого способа оценивания является сложность решения подобной системы уравнений при числе параметров m большем единицы. Поэтому, в данной работе предлагается построение приближения ранговой оценки вектора параметров при помощи численной минимизации функции D.
В статье Л. Джекла Louis A. Jaeckel, Estimating Regression Coefficients by Minimizing the Dispersion of the Residuals// The Annals of Mathematical Statistics, Volume 43, № 5 (1972), 1972, c. 1450 приведена следующая теорема: при фиксированном Y функция D(Y-Xи) - неотрицательная, непрерывная и выпуклая функция и.
В силу этого утверждения, можно искать минимум функции D(Y-Xи) при помощи численных методов по отысканию локального минимума. В данной работе при проведении экспериментов для нахождения минимума функции D используется встроенный в Matlab метод симплексного поиска.
Метод симплексного поиска точки минимума функции k переменных f(z1,..., zK) заключается в выполнении следующих этапов:
- - Сначала выбирается начальное приближение точки минимума z0 = (z10,..., zK0), в дополнение к этой точке генерируются еще k путем прибавления поочередно к каждой компоненте z0 5% ее значения. В точках z0,...,zK вычисляется значение функции f. Эти точки ранжируются по возрастанию значения функции в них, получается набор точек a0,...,aK таких, что f(aI) < f(aj) при i < j. точки a0,...,ak образуют симплекс. - генерируется новая точка r, значение функции в ней сравнивается со значениями функции в вершинах симплекса. если в какой-то вершине значение функции превосходит значение функции в данной точке r, то эта точка становится новой вершиной симплекса, а точка ak с наибольшим значением функции в ней убирается из рассмотрения. имеющиеся вершины снова сортируются по возрастанию значения функции в них. - предыдущий шаг повторяется до тех пор, пока диаметр симплекса не будет меньше заданной величины. по окончании алгоритма в качестве решения задачи минимизации функции выбирается точка a0 из отсортированного набора вершин симплекса.
Данный метод подходит для задачи минимизации функции потерь, поскольку для непрерывных функций позволяет найти локальный минимум с небольшой ошибкой. В силу выпуклости функции любой конечный локальный минимум, даже не единственный, будет являться глобальным минимумом и подходить для оценки параметров.
В книге Т. Хеттманспергера Т. Хеттманспергер "Статистические выводы, основанные на рангах", М.: Финансы и статистика,1987, с. 248 также указано, что диаметр множества точек и, на которых функция достигает минимума, сходится к нулю по вероятности. А это значит, что множество точек, минимизирующих функцию D, будет мало даже при умеренном числе наблюдений.
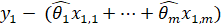
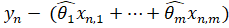
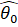
Согласно Т. Хеттманспергеру Т. Хеттманспергер "Статистические выводы, основанные на рангах", М.: Финансы и статистика,1987, с. 257, свободный член и0 в регрессионной модели можно оценить на основании уже полученных оценок параметров и1, ... , иM. Для этого по выборке остатков модели, ... , находится выборочная медиана. Тогда оценка свободного члена равна элементу в середине упорядоченной выборки (если число элементов n нечетное), либо среднему арифметическому двух элементов, находящихся в середине упорядоченной выборки (при четном числе n).
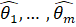
Итак, в этой главе был описан ранговый метод оценивания параметров регрессионной модели и рассмотрены особенности его реализации в данной работе. В приложении № 1 представлен алгоритм для среды Matlab, который строит ранговую оценку параметров регрессионной модели, используя встроенную в Matlab функцию метода симплексного поиска.
Похожие статьи
-
Заключение - Ранговый метод оценивания параметров регрессионной модели
В данной работе был рассмотрен ранговый метод оценивания параметров регрессионной модели, был предложен способ приближенного вычисления ранговой оценки...
-
Введение - Ранговый метод оценивания параметров регрессионной модели
Объектом исследования в этой ВКР является ранговый метод оценивания параметров регрессионной модели. Этот метод применяется при построении регрессионных...
-
Вычисление АОЭ рангового метода по отношению к МНК и МНМ позволяет сделать выводы о том, какой метод лучше применять для оценки параметров в моделях с...
-
Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели
Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...
-
Методы оценки параметров структурной формы модели - Основы эконометрики
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в...
-
Построение модели на реальных данных - Ранговый метод оценивания параметров регрессионной модели
Для построения линейной регрессионной модели на основе реальных данных при помощи рангового метода оценивания параметров был выбран достаточно известный...
-
Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие...
-
Ранговый метод оценивания параметров регрессионной модели
Пример кода, вычисляющий результаты эксперимента по сравнинию ранговой оценки, МНК - и МНМ-оценок параметров для модели с гауссовским распределением...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...
-
Введение, Методы экстраполяции - Формализованные методы прогнозирования
К формализованным методам относятся методы экстраполяции и методы моделирования. Они базируются на математической теории. Среди методов экстраполяции...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...
-
Становление и развитие эконометрического метода на методах вычислительной статистики: - на методах парной и множественной корреляции; - выделение тренда...
-
После проведения регрессионного анализа получается модель объекта исследований в виде некоторой функции. В простейшем случае линейной регрессии она имеет...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Геометрическая интерпретация - Математические методы и модели в экономике
Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...
-
Прогнозирование в регрессионных моделях - Эконометрика как наука
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое...
-
Методы измерения параметров тренда - Ряды динамики в статистике
Тенденция ряда динамики (тренд). Важнейшим направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Введение - Синтез скоринговой модели методом системно-когнитивного анализа
Кредитно-финансовая система является одной из важнейших структур рыночной экономики, так как от темпов ее развития напрямую зависят темпы развития...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Вычисляют выборочную дисперсию, характеризующую меру разброса опытных данных (x I ; Y I ) вокруг значений регрессии, то есть дисперсию остатков ....
-
Аналитические модели, записывающиеся в виде математических конструкций, не включающих логических условий, приводящих к разветвлению вычислительного...
-
Проблема прогнозирования вероятности банкротства существует уже несколько десятков лет - все началось с работ Ramser, Foster (1931), Fitzpatrick (1932) и...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Из перечисленного обзора типов ММ, составляющих предмет ИСО, можно выделить следующие особенности ММ ИСО [3]. - Системный подход, заставляющий...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью...
-
Экспериментальная факторная модель процесса акусто-магнитной обработки топлива
Всевозрастающее воздействие человека на природу привело к возникновению экологических проблем в экосистеме биосферы, в частности, проблемы загрязнения...
-
Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...
-
Итак, модели, которые будут дальше анализироваться, и получены с помощью Первого метода - проведения теста для выделения наиболее дескриптивных...
-
Важным этапом изучения явлений предметов процессов является их классификация, выступающая как система соподчиненных классов объектов, используемая как...
-
Решение транспортной задачи методом потенциалов - Математическая модель решения транспортной задачи
Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены. Пусть имеется транспортная задача с балансовыми условиями...
-
Знаменитая теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ (по первым буквам фамилий ученых), основана на...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Уровень науки и техники Надежность средств, с помощью которых человек достигает космоса высокая, но не идеальна. РН -- сложная конструкция, и даже в...
-
Построение модели с помощью метода деревьев решений - Моделирование вероятности банкротства
В отличие от логистической регрессии, при использовании метода деревьев решений ограничения для независимых переменных отсутствуют, поэтому для...
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели