Нормальное распределение - Элементы теории вероятностей и математической статистики
Наиболее важным распределением для непрерывных случайных величин является нормальное распределение. Множество явлений в практической жизни можно описать с помощью модели нормального распределения. Например, распределение высоты деревьев, площадей садовых участков, массы людей, дневной температуры и т. д. Нормальное распределение используется и для решения многих проблем в экономической жизни. Например, распределение числа дневных продаж в магазине, числа посетителей универмага в неделю, числа работников в некоторой отрасли, объемов выпуска продукции на предприятии и т. д.
Нормальное распределение находит широкое применение и для аппроксимации распределения дискретных случайных величин. Так, например, доходы от определенных видов рискованного бизнеса приблизительно подчиняются нормальному распределению.
Нормальное распределение иногда называют Законом ошибок. Например, отклонения в размерах деталей от установленного размера объясняются многими причинами. Каждая из них влияет на размер детали, так что отклонение, которое фактически регистрируется при измерениях, является суммой большого числа отклонений (ошибок) и следует нормальному закону распределения.
Нормальное распределение (Распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности.
Говорят, что СВ Х Имеет нормальное распределение, если ее плотность вероятности имеет вид:

, (2.13)
Где M и У - параметры распределения, удовлетворяющие соотношениям.
Из (2.13) получаем формулу для функции распределения нормального распределения:

(2.14)
Нормальное распределение зависит от параметров M и У. При этом:
(2.15)
Если СВ Х имеет нормальное распределение с параметрами M и У, то символически это записывается так:
X~N(m, у2) (2.16).
В случае, когда M=0 и У=1, говорят о стандартном нормальном распределении.
Основные свойства плотности вероятности f(x) нормального распределения:
- А) функция F(x) существует при любых действительных значениях Х и принимает только положительные значения. Следовательно, график функции плотности нормального распределения расположен выше оси абсцисс; Б) при неограниченном возрастании Х по абсолютной величине значение F(x) стремится к нулю. Это значит, что ось абсцисс служит горизонтальной асимптотой кривой нормального распределения; В) максимальное значение функция F(x) принимает в точке Х = m, соответствующей математическому ожиданию случайной величины Х; Г) кривая нормального распределения симметрична относительно прямой Х = m, поскольку разность X - m входит в формулу (2.13) во второй степени; Д) кривая нормального распределения имеет две точки перегиба, расположенные симметрично относительно прямой Х = m. Абсциссы точек перегиба M - у и M + у, ординаты точек перегиба .
Формула (2.13) содержит два параметра: математическое ожидание M= М(Х) и стандартное отклонение у = У(X). Следовательно, существует бесконечно много нормально распределенных случайных величин, имеющих разные значения параметров M и У. Графики их плотностей имеют одинаковую форму - симметричную, колоколообразную. Если значения M и У известны, то из семейства нормальных случайных величин выделяют конкретную нормальную случайную величину с определенной плотностью вероятности.
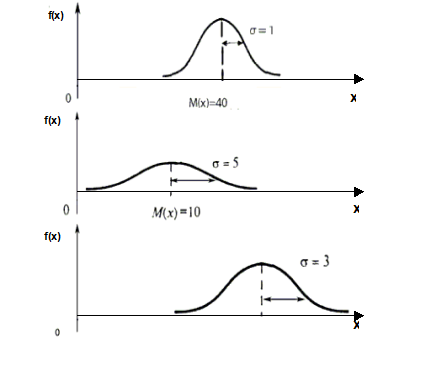
Рис. 2.4. Кривые плотности нормального распределения с различными значениями m и у
Математическое ожидание M - это величина, которая характеризует положение кривой распределения на оси абсцисс (рис. 2.4). Изменение параметра M при неизменном значении у приводит к перемещению оси симметрии (Х = m) вдоль оси абсцисс и, следовательно, к соответствующему перемещению кривой распределения. Значение M иногда называют центром распределения или параметром сдвига. При Х = m функция плотности достигает максимума. Прямая Х = m является осью симметрии. Отметим, что вследствие симметрии она делит пополам площадь, расположенную под кривой плотности. Таким образом, значение M есть мода и медиана распределения Мо = m; Ме = m.
Изменение среднего квадратического отклонения при фиксированном значении математического ожидания приводит к изменению формы кривой распределения. С уменьшением значения У вершина кривой распределения будет подниматься, кривая будет более "островершинной" (вытянутой вдоль оси симметрии). С увеличением значения У кривая распределения менее островершинная и более растянута вдоль оси абсцисс. Одновременное изменение параметров M и У приведет к изменению формы и положения кривой нормального распределения.
Похожие статьи
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Примеры решения - Элементы теории вероятностей и математической статистики
Задача 1. Из 25 контрольных работ, среди которых 5 оценены на "отлично", наугад извлекают 3 работы. Составить закон распределения случайной величины Х -...
-
1. Дифференциальная функция - неотрицательная функция: f(x) ? 0, (2.5), где -? < x <+ ?. Это следует из того, что F ( X ) - неубывающая...
-
Нормальное распределение, также называемое распределением Гаусса, - распределение вероятностей, которое играет важнейшую роль во многих областях знаний,...
-
Цель: освоить на практике нахождение с помощью MS EXCEL числовых характеристик дискретных случайных величин, а также изучить основные свойства функции...
-
Зная плотность распределения F ( X ), можно найти функцию распределения F ( X ) по формуле: . (2.3) Согласно равенствам (2.2), (2.3) и Свойству 6 (л. р....
-
Распределение Пуассона - Элементы теории вероятностей и математической статистики
Распределение Пуассона является дискретным распределением и описывается формулой: , (1.14) Где л>0-параметр распределения. Этот закон используют для...
-
Для функций распределения дискретных и непрерывных случайных величин справедливы свойства, приведенные в л. р. 1. Свойство 4 может быть заменено на...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Цель: Освоить на практике вычисление с помощью MS EXCEL числовых Характеристик случайной непрерывной величины, изучить основные свойства функции...
-
Непрерывные величины - возможные значение, которых непрерывно заполняют некоторый диапазон. Плотность распределения вероятности непрерывной случайной...
-
Распределение Вейбулла, Нормальное распределение - Законы надежности
Двухпараметрическое распределение Вейбулла является более гибким, чем экспоненциальное, которое может рассматриваться как частный случай первого....
-
Моменты распределений дискретных случайных величин. - Распределение вероятности случайных величин
Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится. Не будет лишним помнить, что этот...
-
Пусть у нас имеется некоторая непрерывная случайная величина X, распределенная нормально с математическим ожиданием и среднеквадратичным отклонением....
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
Нормальное распределение - Распределение вероятности случайных величин
Первым, фундаментальным по значимости, является т. н. Нормальный закон Распределения непрерывной случайной величины X, для которой допустимым является...
-
Нормальное распределение - Основы научных исследований
В классической математической статистике чаще всего используется т. н. нормальное распределение или распределение Гаусса-Лапласа. В естествознании и...
-
Распределением признака Называется закономерность встречаемости разных его значений. Нормальное распределение Характеризуется тем, что крайние значения...
-
Контрольная работа По дисциплине: Теория вероятностей Контрольная работа № 1 Вариант 1 Задача № 1 Условие: Из 10 изделий, среди которых 4 бракованные,...
-
Биноминальное распределение - Элементы теории вероятностей и математической статистики
Допустим, что выполняется серия из N независимых одинаковых испытаний. Испытания независимы в том смысле, что результаты одних испытаний не влияют на...
-
Выборочные распределения на шкалах Int и Rel
Оценка наблюдений при неизвестном законе распределения Какова цель наблюдений над случайной величиной; для чего используются результаты наблюдений; где,...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Вопросы по теории вероятностей - Случайные величины
Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. Сумма и произведение событий, теоремы сложения и...
-
Статистическая вероятность и распределения случайных величин - Основы научных исследований
В теории вероятностей под случайной величиной понимают отношения числа благоприятных исходов испытаний к общему числу испытаний. Например, если из 10...
-
Односторонние и двухсторонние значения вероятностей - Распределение вероятности случайных величин
Если нам известен закон распределения СВ (пусть - дискретной), то в этом случае очень часто приходится решать задачи, по крайней мере, трех стандартных...
-
Законы распределений дискретных случайных величин. - Распределение вероятности случайных величин
Пусть некоторая СВ является дискретной, т. е. может принимать лишь фиксированные (на некоторой шкале) значения X I. В этом случае ряд значений...
-
Математическое ожидание - Основы научных исследований
Интегральная и дифференциальная функции распределения являются исчерпывающими статистическими характеристиками любой случайной величины. Однако многие...
-
Обозначим вероятность соответствующих событий через Pi - Случайные величины
, Так как рассматриваемые события образуют полную группу не совместных событий, то Х полностью описана с вероятностной точки зрения, если мы зададим...
-
Распределение (хи-квадрат) - Основы научных исследований
Это распределение, называемое также распределением Пирсона, используется при изучении вероятностных свойств выборочных дисперсий. Если S2(x) - дисперсия...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Прогностическая сила - Базовые результаты математической теории классификации
С целью поиска приемлемого показателя качества диагностики рассмотрим восходящую к Р. Фишеру [20] широко известную параметрическую вероятностную модель...
-
В решении любой прикладной задачи можно выделить три основных этапа: - Построение математической модели исследуемого объекта - Выбор способа и алгоритма...
-
Методы непараметрической статистики - Основы теории систем и системного анализа
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что...
-
Метод максимального правдоподобия - Основы научных исследований
Разработан Р. Фишером. Пусть Х 1 ,х 2 ...х N - выборка из генеральной совокупности случайной величины Х с функцией плотности вероятности Р(х, и),...
-
Монте карло погрешность распределение интеграл В качестве оценки интеграла принимают , Где n - число испытаний; F(x) - плотность распределения...
-
применяем 2е теоремы: -формула полной вероятности Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H1, H2, ..., Hn...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
-
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах...
-
Системы массового обслуживания -- это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки...
Нормальное распределение - Элементы теории вероятностей и математической статистики