Введение, Физическая модель, Математическая модель - Изучение распределения температуры в тонком цилиндрическом стержне
В решении любой прикладной задачи можно выделить три основных этапа:
- - Построение математической модели исследуемого объекта - Выбор способа и алгоритма решения полученной модели - Численная реализация алгоритма
Цель данной работы - на примере исследования распределения температуры в тонком цилиндрическом стержне освоить основные методы приближенных вычислений, приобрести практические навыки.
Самостоятельных исследований, существенно опирающихся на использование методов прикладной математики.
Физическая модель
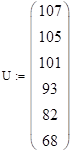
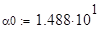
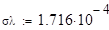
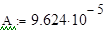
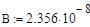
При решении некоторых практических задач возникает необходимость исследования распределения температуры вдоль тонкого цилиндрического стержня, помещенного в высокотемпературный поток жидкости или газа. Такое исследование можно проводить на основе обработки эксперимента (измерение температуры в различных точках стержня) или путем анализа соответствующей математической модели.
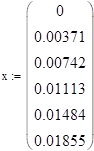
В настоящей работе используется оба подхода.
В нашем случае, тонкий цилиндрический стержень помещен в постоянный тепловой поток (с температурой ). На концах стержня поддерживается постоянная температура.
Математическая модель
Совместим координатную ось абсцисс с продольной осью стержня с началом в середине стержня. Будем рассматривать задачу (распределение температуры по стержню)
После момента установление режима.
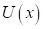
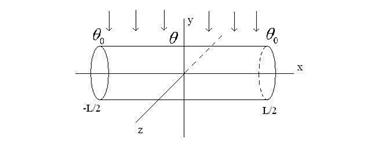
Первая математическая модель использует экспериментальные данные, при этом измеряют температуру стержня в нескольких точках стержня с координатами. Результаты измерения рассматривают как функцию регрессии и получают статистики. Учитывая четность можно искать ее в виде многочлена по четным степеням (ограничимся 4-ой степенью этого многочлена).
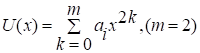
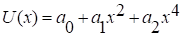
(1.1)
Задача сводится к отысканию оценок неизвестных параметров, т. е. коэффициентов и, например, методом наименьших квадратов.
Вторая математическая модель основана на использовании закона теплофизики. Можно доказать, что искомая функция имеет вид:
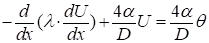
(1.2)
Где - коэффициент теплопроводности, - коэффициент теплоотдачи, - диаметр стержня, - температура потока, в который помещен стержень.
Ищем как решение краевой задачи для уравнения (1.2) с граничными условиями:
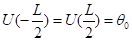
(1.3)
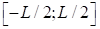
На отрезке, где L-длина стержня, - постоянная температура, поддерживаемая на концах стержня.
Коэффициент теплопроводности зависит от температуры:
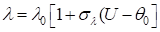
(1.4)
Где - начальное значение коэффициента теплопроводности, - вспомогательный коэффициент.
Коэффициент теплоотдачи вычисляют по формуле:
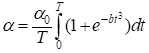
(1.5)
Т. е. как среднее значение функции
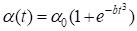
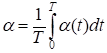
За некоторый отрезок времени от 0 до Т, здесь - значение при t стремящемся к бесконечности, b - известный коэффициент.
Время, по истечении которого распределение температуры в стержне можно считать установившимся определяется по формуле:
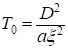
(1.6)
Где а - коэффициент температуропроводности, - наименьший положительный корень уравнения:
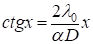
(1.7)
Похожие статьи
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
Имеется выборка объема n экспериментальных значений. Предполагаем, что ошибки вычисления пренебрежимо малы, а случайные ошибки измерения температур...
-
Интерполяция является одной из задач Приближения функции. В общем случае сводит более сложную функцию к более простой. Интерполяция - замена одной...
-
Введение - Моделирование математической модели теплообменника
Математический динамический модель канал Качественные и количественные изменения в промышленности, науке и технике составляют основу для значительного...
-
Введение - Ранговый метод оценивания параметров регрессионной модели
Объектом исследования в этой ВКР является ранговый метод оценивания параметров регрессионной модели. Этот метод применяется при построении регрессионных...
-
С началом пилотируемого освоения космоса возникла задача обеспечения безопасности человека и возвращения его на Землю. Основная опасность грозила...
-
Современные экономические теории и исследования опираются в значительной степени на использование математических моделей и методов анализа. Постоянно...
-
Геометрическая интерпретация - Математические методы и модели в экономике
Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...
-
Введение - Экономико-математические методы
Экономические проблемы, возникающие перед специалистами, в большинстве своем сложные. Они зависят от множества различных, иногда противоречащих друг...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
В анализе экономического состояния и предприятия, и более крупного субъекта национального хозяйства применяется расчленение проблемы, или ситуации на...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
В 2011 - 2015 гг. в серии статей в научных журналах и докладов на международных, зарубежных и всероссийских научных конференциях была представлена...
-
1. Универсальность - характеризует полноту отображения моделью изучаемых свойств реального объекта. 2. Адекватность - способность отражать нужные...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
Введение - Эконометрические модели маркетинговой деятельности на предприятии
Процесс моделирования имеет несколько этапов. Содержательная постановка задачи - формулируются вопросы, на которые надо получить ответы. Делаются...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
Двумерная математическая модель жидкости водоема с учетом наличия на поверхности ледяной пластины
Введение В данной работе рассматривается численная модель движения в двумерных (в вертикальной плоскости) водоемах. Математическая модель основана на...
-
Как известно, человечество в своем стремительном развитии старается все более расширить сферы своей деятельности, сталкиваясь при этом с множеством новых...
-
Введение - Математические методы и модели в экономике
Основу коммерческой деятельности торгового предприятия на потребительском рынке составляет процесс продажи товаров. Экономическое содержание этого...
-
Введение - Физические и химические свойства кремния
Кремний - широко распространенный элемент в природе. В земной коре его 27.6%. атомный вес кремния 28.06. температура плавления 1415°C, температура...
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
Выбор математической формы функции при моделировании зависимости выпуска продукции от производственных факторов Постановка проблемы. Одним из важнейших...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Введение, Введение в эконометрику - Моделирование в эконометрике
Эконометрика - наука, исследующая количественные закономерности и взаимозависимости в экономике при помощи методов математической статистики. Основа этих...
-
ВВЕДЕНИЕ - Математическая модель роста экономики Краснодарского края
В наше время математическое моделирование используется во всех отраслях науки. В своей дипломной работе, с помощью математического моделирования, я...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
Z -преобразование является одним из математических методов, разработанных для анализа и проектирования дискретных систем. Аппарат Z -преобразования...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Методы классификации - неотъемлемая часть математических методов исследования, интересная теоретически и важная практически. Обзоры этой научной области...
-
Введение - Построение экономических моделей
Современные экономические теории и исследования опираются в значительной степени на использование математических моделей и методов анализа. Постоянно...
-
Маркетинговое исследование представляет собой системный сбор, обработку и анализ всех аспектов процесса маркетинга: продукта, его рынка, каналов...
-
Планирование и прогнозирование являются одними из важнейших задач любого предприятия. Особенно актуальными эти аспекты делают нестабильность...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Классификация математических моделей - Построение и классификация математических моделей
К классификации математических моделей разные авторы подходят по-своему, положив в основу классификации различные принципы. Можно классифицировать...
-
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью...
Введение, Физическая модель, Математическая модель - Изучение распределения температуры в тонком цилиндрическом стержне