Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически.
Случай двух переменных не имеет особого практического значения, но его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
Пусть дана задача:
Z=c1x1+c2x2 max (2.6)
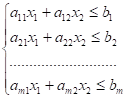
(2.7)
(2.8)
Дадим геометрическую интерпретацию элементов этой задачи.
Введем на плоскости декартову прямоугольную систему координат x1Ox2 и сопоставим каждой паре чисел (x1,x2) точку плоскости с координатами x1 и х2. Выясним сначала, что представляет собой множество точек, соответствующих допустимым решениям данной задачи.
Рассмотрим одно линейное неравенство.
Оно определяет на плоскости одну из двух полуплоскостей, на которые прямая разбивает плоскость (сторона в которой располагается полуплоскость от прямой, указывается штриховкой).
Убедиться в том, с какой стороны от прямой лежит полуплоскость, точки которой удовлетворяют заданному неравенству, можно путем подстановки координат точек одной или другой полуплоскости в неравенство. Если координаты точки удовлетворяют неравенству, то эта точка лежит в полуплоскости, соответствующей данному неравенству. В противном случае неравенству соответствует другая плоскость.
Каждое из ограничений (2.7), (2.8) задает на плоскости х1Oх2 некоторую полуплоскость. Нас интересуют те точки плоскости, координаты которых принадлежат всем полуплоскостям. Следовательно, допустимое множество ЗЛП геометрически изображается пересечением (общей частью) полуплоскостей, определяемых отдельными ограничениями. Полуплоскость - выпуклое множество. Множество называется выпуклым, если ему вместе с двумя произвольными точками принадлежит и прямолинейный отрезок, их соединяющий. Пересечение любого числа выпуклых множеств является выпуклым множеством. Таким образом, область допустимых решений задачи (2.6) - (2.8) есть выпуклое множество. На рис.2.1 представлены возможные ситуации, когда область допустимых решений ЗЛП - выпуклый многоугольник (а), неограниченная выпуклая многоугольная область (б), единственная точка (в), прямая линия (г), луч (д), отрезок (е), пустое множество (ж).
X2 X2
б)
0 а) X1 0 X1
Х2 Х2 Х2
в) 1 д)
г)
0 Х1 0 Х1 0 Х 1
Х2 Х2
е) ж)
Х1
0 0 Х1
Рис.2.1
Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП - непустое множество, например, многоугольник ABCDE рис.2.2.
X2
B C
M
A
D
E
0 X1
Рис.2.2 N
Рис.2.2 N
Выберем произвольное значение целевой функции Z=Z0. Получим
C1x1+c2x2=Z0
Это уравнение прямой линии (рис.2.2 - прямая MN). В точках прямой MN целевая функция сохраняет одно и то же постоянное значение Z0.
Считая Z0 параметром, получим семейство параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения). Нас интересуют те точки области допустимых решений, которые принадлежат линии уровня с наибольшим значением Z0 по сравнению с его значениями для всех других линий уровня, пересекающихся с областью допустимых решений.
Возникает вопрос: как установить направление возрастания (убывания) целевой функции по x1 и х2 :
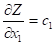
(2.9)
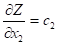
(2.10)
Частная производная (2.9) и (2.10) функции показывает скорость ее возрастания вдоль данной оси. Следовательно, с1 и с2 - скорости возрастания вдоль осей Oх1 и Oх2. Вектор называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор - указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом. Вектор перпендикулярен к прямым Z = const семейства
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1, С учетом системы ограничений строим область допустимых решений.
Строим вектор наискорейшего возрастания целевой функции.
Проводим произвольную линию уровня Z=Z0, перпендикулярную к вектору так, чтобы она пересеклась с областью допустимых решений.
При решении задач на max перемещаем линю уровня Z=Z0 в направлении вектора так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точки) (на рис.2.2 точка С). В случае решения задачи на min линию уровня Z=Z0 перемещают в направлении вектора - (на рис.2.2 - точка Е).
Определяем оптимальный план и экстремальное значение целевой функции.
Пример 2.1.
Предприятию необходимо изготовить два вида продукции А и В, с использованием трех видов ресурсов R1, R2, R3 количество которых ограничено. Исходные данные задачи представлены в таблице:
|
Вид ресурсов |
Количество ресурсов, идущих на изготовление единицы продукции |
Запасы ресурсов | |
|
А |
В | ||
|
R1 |
6 |
6 |
36 |
|
R2 |
4 |
2 |
20 |
|
R3 |
4 |
8 |
40 |
|
Доходы от реализации продукции |
12 |
15 |
Требуется составить такой план выпуска продукции, чтобы при ее реализации получить максимальный доход.
Решение.
Обозначим через х1 и х2 количество единиц продукции видов А и В, планируемых к выпуску.
Известно, что доход от реализации единицы продукции А составляет 12 усл. ед. и количество этой продукции - х1. Следовательно, доход от реализации всей продукции А составит 12х1 усл. ед. Аналогично, доход от реализации всей продукции В составит 15х2 усл. ед. Учитывая, что доход от реализации продукции должен быть максимальным, целевая функция задачи будет иметь вид:
Известно также, что имеющиеся на предприятии ресурсы ограничены. Это обстоятельство в свою очередь необходимо отразить в модели. Предприятие производит продукцию, используя три вида ресурсов. Естественно, что фактический расход никакого вида ресурса не должен превышать запасов соответствующего вида ресурсов на предприятии. Поскольку расход каждого вида ресурсов на единицу каждого вида продукции и запасы ресурсов известны, это обстоятельство отражается в следующих ограничениях:
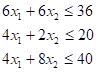
Смысл первого ограничения состоит в том, что фактический расход ресурса R1 на производство продукции А и В, равный 6х1+6х2 (здесь 6х1 - количество единиц ресурса R1, идущего на изготовление х1 единиц продукции A; 6х2 - количество единиц ресурса R1, идущее на изготовление х2 единиц продукции В) не должен превышать запаса этого ресурса на предприятии, равного 36 ед. Аналогичный смысл имеют 2-е и 3-е ограничения только для ресурсов R2 и R3 соответственно.
Количество продукции, выпускаемое предприятием, должно быть величиной положительной или равной нулю (если предприятие определенный вид продукции не производит). Следовательно, в модели должны присутствовать ограничения неотрицательности переменных:
Таким образом, построена математическая модель нашей задачи как задачи линейного программирования:
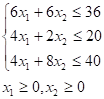
Начнем решение задачи с построения области допустимых решений (рис.2.3)
В первую очередь отобразим в прямоугольной системе координат условия неотрицательности переменных. В двумерном пространстве уравнению соответствует прямая линия, а неравенству - полуплоскость, лежащая по одну сторону от прямой. Прямые х1=0 и х2=0 совпадают с осями координат. Полуплоскости x1>0,x2>0 лежат соответственно справа от оси Oх2 и выше оси Oх1. Множество точек, удовлетворяющих одновременно неравенствам представляют собой пересечение построенных полуплоскостей вместе с граничными прямыми и совпадают с точками первой четверти.
Теперь рассмотрим ограничения задачи. Построим по порядку прямые:
- 6x1+6x2=36 или х1+х2=6 (а) 4х1+2х2=20 или 2х2+х2=10 (б) 4х1+8х2=40 или х1+2х2=10 (в)
И определяем, с какой стороны от этих прямых лежат полуплоскости, точки которых удовлетворяют строгим неравенствам:
- 6x1+6x2 4x1+2x2 4x1+8x2
Для определения полуплоскости решений первого неравенства возьмем произвольную точку плоскости, не лежащую на прямой 6х1+6х2=36, например (0;0), и подставим ее координаты в неравенство.
В результате подстановки получили верное числовое неравенство 0< 36, и это означает, что начало координат лежит в полуплоскости решений первого неравенства. Сторона, в которой располагается полуплоскость от прямой, указывается штриховой.
Аналогично строим полуплоскость решений остальных неравенств.
X2
б)
a) N2
в) M
*6
в
0 N
C x1
6
D
Рис.2.3
Заштрихованная часть плоскости и представляет собой искомый многоугольник допустимых решений задачи (рис.2.3)
Теперь нужно среди точек построенного многоугольника найти такую, в которой целевая функция Z=12x1+15x2 достигает максимального значения. Для этого построим прямую, заданную уравнением 12х1+15х2=0, которая является линией нулевого уровня функции Z.
Направление возрастания линейной функции Z=12x1+15x2 указывает вектор с началом в точке (0;0) и концом в точке М1(12,15), координаты которой равны коэффициентам при соответствующих переменных функции Z.
Для нахождения оптимального плана нужно "передвигать" линию нулевого уровня Z параллельно самой себе в направлении вектора до точки ее "последней встречи" с многоугольником, которая и является оптимальным планом задачи. В нашем случае это вершина В многоугольника OABCD - точка пересечения прямых (а) и (в). Координаты ( ) точки найдем, решив систему уравнений.
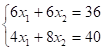
откуда х1*=2, х2*=4.
Найдем соответствующее значение целевой функции:
усл. ед.
Ответ. Для обеспечения максимального дохода от реализации готовой продукции предприятию необходимо выпустить 2 ед. продукции вида А и 4 ед. продукции вида В. При таком плане доход от реализации составит 84 усл. ед.
Геометрический метод решения ЗЛП обладает рядом достоинств: он прост, нагляден, позволяет быстро и легко получить ответ. Однако только геометрический метод решения никак не может удовлетворить ни математиков, ни экономистов. Возможны "технические" погрешности, которые неизбежно возникают при приближенном построении графиков. Второй недостаток геометрического метода заключается в том, что многие величины, имеющие четкий экономический смысл (такие, как остатки ресурсов производства, избыток питательных веществ и т. п.), не выявляются при геометрическом решении задач. Но самое главное - геометрический метод неприемлем для решения практических задач. Поэтому необходимы аналитические методы, позволяющие решать ЗЛП с любым числом переменных и выявить экономический смысл входящих в них величин.
Похожие статьи
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Геометрическая интерпретация - Математические методы и модели в экономике
Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Решение: Строим на плоскости х1Ох2 многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки...
-
Во многих экономических моделях исследования операций зависимости между постоянными и переменными факторами лишь в первом приближении можно считать...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
МЕТОДЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ - Основы моделирования геометрических объектов
Если прямая параллельна одной из плоскостей проекций т. е. является прямой уровня, то без преобразования ортогональных проекций можно только найти...
-
Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий,...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Метод множителей Лагранжа - Экономико-математические методы
Среди задач (4.1)-(4.3) особое место занимают задачи типа (6.10) , (6.11) Для решения которых можно воспользоваться классическим методом оптимизации...
-
Геометрический метод - Интегральное и дифференциальное исчисление
Теоретическое введение: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
ПЛОСКОСТЬ, СПОСОБЫ ГРАФИЧЕСКОГО ЗАДАНИЯ ПЛОСКОСТЕЙ - Основы моделирования геометрических объектов
Плоскость - одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий,...
-
Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси...
-
МЕТОД ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ - Основы моделирования геометрических объектов
Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Линейное программирование в экономике - Экономико-математические методы
Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, фирма и т. д.), исходя из конъюнктуры рынка, технических...
-
МЕТОД МОНЖА - Основы моделирования геометрических объектов
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Параметрическое линейное программирование - Методы линейного программирования
Представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или...
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ - Основы моделирования геометрических объектов
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических...
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы