Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной, Планиметрические задачи - Применение производной в решении геометрических задач
Планиметрические задачи
Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если:
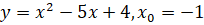
[3].
Решение. Уравнение касательной будем искать по формуле ; уравнение нормали - по формуле По условию, .
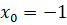
.
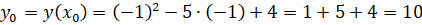
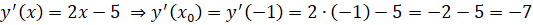
.
Подставляем все найденные значения в уравнение касательной:
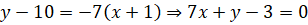
.
Теперь находим уравнение нормали:
.
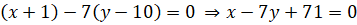
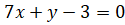
Ответ: уравнение касательной:; уравнение нормали:
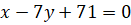
.
Задача 2.Написать уравнения касательной и нормали в точке
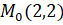
К кривой
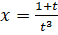
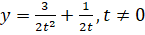
, [3].
Решение:
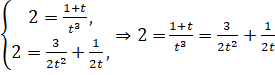
Решим уравнение
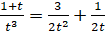
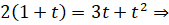
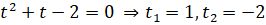
.
Подставим полученные решения в равенство
:
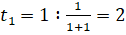
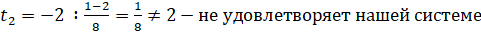
.
Найдем производную функции, заданной параметрически.
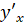
;
.
;
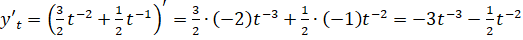
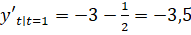
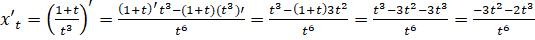
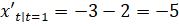
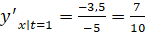
.
Подставляем все найденные значение в уравнение касательной:
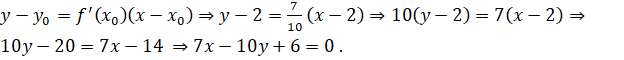
Теперь находим уравнение нормали:
.
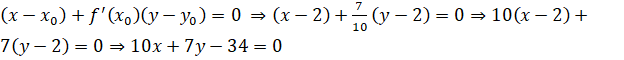
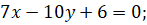
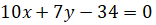
Ответ: Уравнение касательной: уравнение нормали: .
Задача 3. Найти углы, под которыми пересекаются заданные кривые:
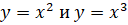
[3].
Решение. Угол между кривыми находится по формуле
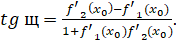
Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:
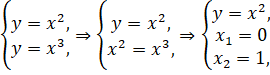
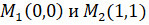
Таким образом, кривые пересекаются в точках.
Далее найдем значения производных заданных функций в точках пересечения.
Производный дифференцирование уравнение планиметрический
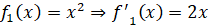
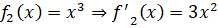
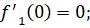
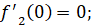
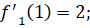
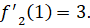
Подставляем найденные значение в формулу нахождения угла:
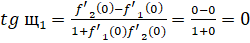
.
Следовательно, .
.
Следовательно, .
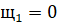
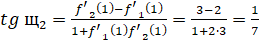

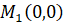

Ответ: в точке угол равен 0 (т. е. касательные совпадают), в точке угол равен.
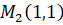
Задача 4. Задан прямоугольник с периметром 56 см. Каковы должны быть его стороны, чтобы площадь была наибольшей [7]?
Решение.
Обозначим одну из сторон за, тогда вторая сторона:
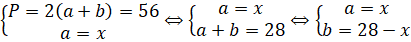
Площадь такого прямоугольника составит:
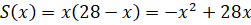
.
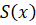
Требуется найти максимум функции.
Это квадратичная функция, ее график - парабола, ветви которой направлены вниз.
Найдем производную:
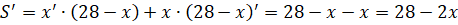
.
Определим критические точки: .
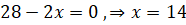
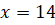
Так, - точка экстремума, слева от нее производная положительна, а справа - отрицательна.
Очевидно, что - точка максимума. В таком случае площадь прямоугольника максимальна, когда его стороны равны 14 см, то есть когда он является квадратом.
Ответ: площадь максимальна, когда стороны прямоугольника равны 14 см.
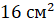
Задача 5. Площадь прямоугольника составляет. Каковы должны быть его размеры этого прямоугольника, чтобы периметр был минимальным?[7]
Решение.
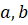
Пусть стороны прямоугольника равны. Тогда:
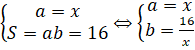
Периметр такого прямоугольника составит:
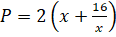
Требуется найти минимум данной функции. Найдем производную:
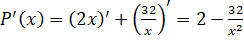
Найдем точки экстремума:
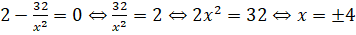
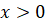
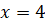
Очевидно, что, поэтому нас интересует точка. Слева от нее производная отрицательна, а справа - положительна.
Так, - точка минимума.
Ответ: чтобы периметр прямоугольника был минимальным, его стороны должны составить 4 см.
Задача 6. Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне. Найти условия, при которых площадь параллелограмма является наибольшей [2].
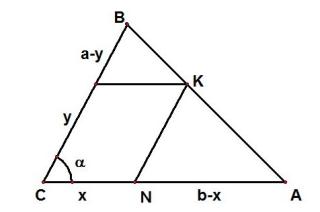
Рис.4
Решение.
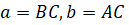
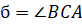
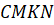
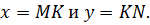
Пусть треугольник определяется двумя сторонами и углом между ними (рис.4). Построим параллелограмм в соответствии с условиями задачи. Обозначим стороны параллелограмма Площадь параллелограмма определяется формулой
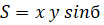
.
Выразим через и стороны треугольника. Из подобия треугольников и следует, что
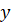
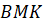
Тогда
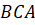
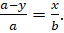
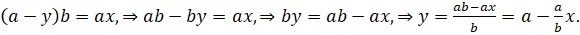
В результате площадь записывается как функция:
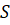
Находим производную:
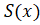
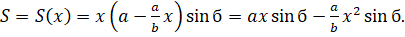
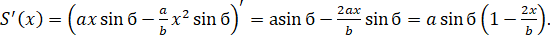
Отсюда видно, что экстремум функциисуществует в следующей точке:
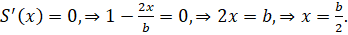
При переходе через эту точку производная меняет свой знак с плюса на минус, то есть эта точка является точкой максимума. Другая сторона параллелограмма при этом равна
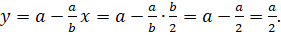
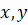
Итак, вписанный в треугольник параллелограмм со сторонами имеет наибольшую площадь при условии
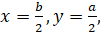
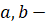
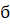
Где стороны треугольника. Интересно, что результат не зависит от угла между сторонами треугольника.
Ответ: площадь параллелограмма является наибольшей при условии
Где стороны треугольника.
Задача 7.Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром [2].
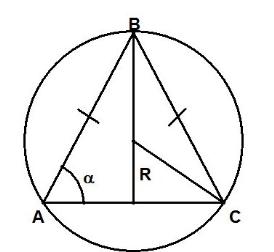
Рис.5
Решение.
Пусть треугольник вписан в окружность данного радиуса,
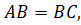
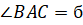
(независимая переменная) (рис.5). Выразим периметр треугольника как функцию. По теореме синусов:
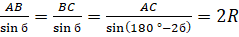
, отсюда
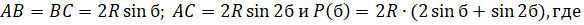
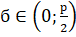
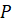
. Найдем, при каком значении функция принимает наибольшее значение на данном интервале
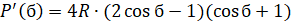
.
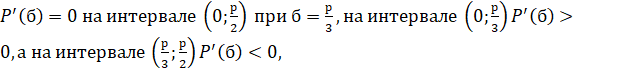
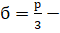
Следовательно, точка максимума, в которой функция принимает наибольшее значение на заданном промежутке. Таким образом, наибольший периметр имеет равносторонний треугольник.
Ответ: среди всех равнобедренных треугольник, вписанных в данную окружность, с наибольшим периметром является равносторонний треугольник.
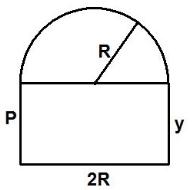
Рис.6
Задача 8.Окно имеет форму прямоугольника, ограниченного сверху полукругом.
Периметр окна равен. Определить радиус полукруга, при котором площадь окна является наибольшей (рис.6) [2].
Решение.

Очевидно, что одна сторона прямоугольника равна. Другую сторону обозначим через. Периметр всего окна выражается формулой
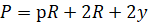
Отсюда находим :
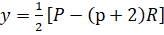
Площадь окна составляет:
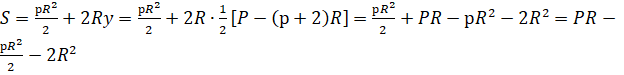
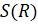
Полученное выражение представляет собой функцию. Исследуем ее на экстремум. Находим производную:
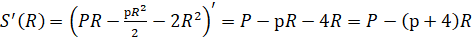
Определяем стационарные точки:
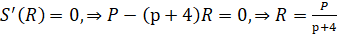
Поскольку вторая производная отрицательна:
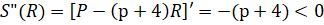
,
То найденная точка является точкой максимума, т. е. при этом значении площадь окна будет наибольшей.
Само максимальное значение площади составляет
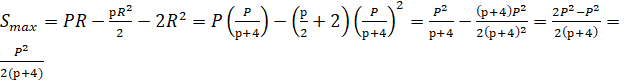
.
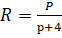
Ответ: радиус полукруга, при котором площадь является наибольшей.
Похожие статьи
-
Стереометрические задачи - Применение производной в решении геометрических задач
Рис.7 Задача 1.Определить наибольший объем цилиндра, вписанного в конус с радиусом основания и высотой [4]. Решение. Обозначим радиус основания...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Заключение, Список литературы - Применение производной в решении геометрических задач
В данной работе рассмотрено решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной. В процессе выполнения...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Исторические сведения о производной - Применение производной в решении геометрических задач
Ряд задач дифференциального счисления был решен еще в древности. Такие задачи можно найти у Евклида и у Архимеда, но само понятие производной функции...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
Интерполяция является одной из задач Приближения функции. В общем случае сводит более сложную функцию к более простой. Интерполяция - замена одной...
-
Исследование разрешимости второй краевой задачи для уравнения в частных производных с инволютивным отклонением в младших членах Многие математические...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Все генетические алгоритмы участвовали в двух группах тестов. В каждой группе исследовались различные наборы значений управляющих параметров МГА:...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Тема, с которой мы сегодня ознакомимся это "Применение матриц при решении экономических задач." Рассмотрим как с помощью матриц можно решать...
-
Задание №1 Найти матрицу АВ+3Е и ВА+3Е, где , , Е - единичная матрица соответствующего порядка. Решение: Найти матрицу АВ+3Е 1.1 Найдем размер матрицы...
-
Метод множителей Лагранжа - Экономико-математические методы
Среди задач (4.1)-(4.3) особое место занимают задачи типа (6.10) , (6.11) Для решения которых можно воспользоваться классическим методом оптимизации...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера. Определение 3.1. Функцией Эйлера называется функция, определенная на...
-
Геометрическая интерпретация - Математические методы и модели в экономике
Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной, Планиметрические задачи - Применение производной в решении геометрических задач