Принцип Дирихле - Разработка контрольных работ по математике
В математике большое значение имеют так называемые доказательства существования. Самый простой способ доказать существование объекта с заданными свойствами - это указать его и, разумеется, убедиться, что он действительно обладает нужными свойствами. Например, чтобы доказать, что уравнение имеет решение достаточно привести какое-то его решение. Доказательства существования такого рода называют прямыми или конструктивными.
Но бывают и косвенные доказательства существования, когда обоснование факта, что искомый объект существует, происходит без прямого указания на сам объект.
Одним из способов косвенно доказать существование является логический прием названный принципом Дирихле - по имени Петера Густава Дирихле, немецкого математика. Принцип устанавливает связь между объектами ("кроликами") и контейнерами ("клетками") при выполнении определенных условий.
В самой простой и несерьезной форме он выглядит так:
Нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев.
Действительно, если в каждой клетке не больше двух зайцев, то всего зайцев не больше чем 2*3=6, что противоречит условию.
Существует более общая формулировка:
Если z зайцев сидят в k клетках, то найдется клетка, в которой не менее z/k зайцев. Не надо бояться дробного число зайцев: если получается, что в ящике не меньше 7/3 зайцев, значит, их больше двух.
Доказательство принципа Дирихле в этой формулировке очень простое, но заслуживает внимания, поскольку похожие рассуждения "от противного" часто встречаются. Допустим, что в каждой клетке число зайцев меньше, чем z/k. Тогда в k клетках зайцев меньше, чем k - z/k = z. Получили противоречие.
Принцип Дирихле известен также как принцип голубей и ящиков, когда объектами являются голуби, а клетками -- ящики. Это название распространено в английском и некоторых других языках.
Вот общая формулировка принципа Дирихле:
Если имеется n ящиков, в которых находится в общей сложности не менее n+1 предмета, то непременно есть ящик, в котором лежат, по крайней мере, 2 предмета.
Рассмотрим несколько задач, для решения которых необходимо применить этот принцип, выбирая каждый раз подходящих "зайцев" и строя соответствующие "клетки".
Задача 1
В самолете летят 380 пассажиров. Докажем, что, по крайней мере, двое из них родились в один и тот же день года.
Решение. Всего в году 365 или 366 дней, а пассажиров в самолете 380 - значит, их дни рождения не могут приходиться только на различные даты. Вообще, если пассажиров больше, чем 366, то хотя бы у двоих дни рождения совпадают. А вот если пассажиров 366, не исключено, что все они родились в разные дни года, но это маловероятно. (Согласно теории вероятностей, в случайно выбранной группе численностью свыше 22 человек совпадение дней рождения у некоторых из них более вероятно, нежели то, что у всех дни рождения приходятся на разные дни года).
Задача 2
В шахматной партии черные сдались после 15-го хода белых. Требуется доказать, что хотя бы одна из черных фигур ни разу не покидала своего поля (к фигурам отнесем и пешки).
Решение. Если шахматный ход не рокировка (обмен местами), то передвигается одна фигура, в случае рокировки - две. Черные успели сделать 14 ходов (так как первыми ходят белые), и по правилам игры лишь один из них мог быть рокировкой. Поэтому самое большое количество черных фигур, сделавших ходы, - 15. Всего же черных фигур 16. Значит, по крайней мере, какая-то из них не сделала ни одного хода.
В первом примере таким "ящиками" были дни года, а "предметами" - даты рождения пассажиров, летевших в самолете. Во втором, мы "раскладывали" все черные фигуры ("предметы") по максимальному количеству их ходов ("ящикам"). То есть каждой фигуре ставили в соответствие один неповторимый ход, но фигур оказалось на одну больше, чем ходов, таким образом "ящиков" оказалось на один меньше, чем "предметов".
Рассмотрим решение еще нескольких задач.
Задача 3
В строку выписано 5 натуральных чисел: a1,a2,a3,a4,a5. Докажите, что - либо одно из них делится на 5, либо сумма нескольких рядом стоящих чисел делится на 5.
Решение. Рассмотрим 5 чисел: а1,
А1+а2,
А1+а2+а3,
А1 +а2+а3+а4,
А1 +а2+а3+а4+а5.
Если одно из них делится на 5, то все в порядке, утверждение справедливо. В противном случае при делении на 5 они дают в остатке какие-то из четырех чисел: 1,2,3,4. По принципу Дирихле остатки, по крайней мере, двух из выписанных 5 чисел совпадают. Разность их делится на 5. Но эта разность - одно из чисел, данных в задаче, или сумма нескольких из них, стоящих рядом.
Задача 4
В квадрат со стороной 1 м бросили произвольным способом 51 точку. Докажите, что какие-то три из них можно накрыть квадратиком со стороной 0,2 м.
Решение. Разобьем квадрат на 25 равных квадратиков со стороной 0,2м. Докажем, что в каком-то из них находятся, по крайней мере, три точки. Применим принцип Дирихле: если бы в каждом квадратике (внутри или на сторонах) было не больше двух точек, то всего их бы было не больше 2*25=50. Но всего бросили в квадрат 51 точку. Получили противоречие.
Задача 5
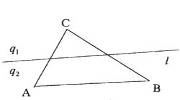
Доказать, что если прямая l, расположенная в плоскости треугольника ABC, не проходит ни через одну из его вершин, то она не может пересечь все три стороны треугольника.
Решение. Полуплоскости, на которые прямая l разбивает плоскость треугольника ABC, обозначим через q1 и q2; эти полуплоскости будем считать открытыми (то есть не содержащими точек прямой l). Вершины рассматриваемого треугольника (точки A, B, C) будут "зайцами", а полуплоскости q1 и q2 - "клетками". Каждый "заяц" попадает в какую-нибудь "клетку" (ведь прямая l не проходит ни через одну из точек A, B, C). Так как "зайцев" три, а "клеток" только две, то найдутся два "зайца", попавшие в одну "клетку"; иначе говоря, найдутся такие две вершины треугольника ABC, которые принадлежат одной полуплоскости.
Пусть, скажем, точки A и B находятся в одной полуплоскости, то есть лежат по одну сторону от прямой l. Тогда отрезок AB не пересекается с l. Итак, в треугольнике ABC нашлась сторона, которая не пересекается с прямой l.
Другое применение принципа Дирихле
Принцип Дирихле можно применять при решении задач на знакомства;
Пример: доказать, что среди 5 человек, по крайней мере двое из них имеют одинаковое число знакомых среди выбранных.
Указание. Рассматриваются все возможные варианты количества знакомых данных 5 человек.
Задач на делимость;
Пример: Доказать, что среди любых 12 натуральных чисел можно выбрать 2, разность которых делится на 11.
Указание. Рассматриваются все возможные остатки при делении числа на 11. геометрических задач (задача 4, 5).
Контрольная работа №2 для учащихся 8 классов
Приведенные ниже задания являются контрольной работой №2 для учащихся 8 классов. Каждая задача оценивается в 5 баллов, для зачета нужно набрать не менее 25 баллов.
Правила оформления работ:
Решения по каждому предмету оформляется отдельно. Каждое задание имеет свой шифр (М 8.2.1 и т. д.), который указывается перед записью решения. Переписывать текст задачи не надо, достаточно краткой записи, если это необходимо. Оформлять решения в порядке следования заданий. Можно присылать нам столько решений, сколько удалось вам сделать, даже если оказалось невозможным выполнить всю работу.
В классе 30 человек. В диктанте Вова сделал 13 ошибок, а остальные - меньше. Докажите, что по крайней мере 3 ученика сделали ошибок поровну (может быть, по 0 ошибок).
В классе 40 учеников. Найдется ли такой месяц в году, в котором отмечают свой день рождения не меньше чем 4 ученика этого класса?
Докажите, что из любых трех целых чисел можно выбрать два, сумма которых четна.
Докажите, что из любых 10 натуральных чисел, ни одно из которых не делится на 10, можно выбрать 2 числа, разность которых делится на 10.
В поход пошли 20 туристов. Самому старшему из них 35 лет, а самому младшему а) 16 лет б) 17 лет. Верно ли, что среди туристов есть одногодки?
Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся команды, сыгравшие к этому моменту одинаковое количество матчей.
Каждый из 10 участников переговоров послал по их окончании поздравительные открытки пятерым другим участникам. Докажите, что какие-то двое послали открытки друг другу.
Указание. Докажите сначала, что хотя бы один участник получил не менее пяти открыток.
На шахматной доске стоят 44 ферзя. Докажите, что каждый из них бьет какого-нибудь другого ферзя.
Указание. При любом положении на доске ферзь бьет не менее 21 поля.
На плоскости нарисовали 5 прямых. Докажите, что угол между какими-то двумя из них не больше 36°. (Если какие-нибудь прямые параллельны, считайте, что угол между ними равен 0°.)
Указание. Угол между прямыми не изменяется, если к ним применить параллельный перенос (для каждой прямой -- свой перенос).
Найдите значение дроби
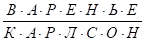
,
Где разные буквы -- это разные цифры.
Указание. В дроби записаны 10 разных букв, соответствующие 10 различным цифрам.
Элементы теории сравнений
Изучение свойств целых чисел было начато математиками давно ушедших поколений. По мере развития математической науки эти проблемы стали решаться в рамках целого математического раздела - теории чисел. На современном этапе развития информационного общества, когда наблюдается быстрое развитие новых информационных технологий, некоторые вопросы теории чисел, интересовавшие ранее только специалистов-математиков превратились в новое направление "вычислительной теорию чисел". Одним из разделов этого направления является теория сравнений.
В этой статье мы рассмотрим основные понятия этой теории, их свойства и некоторые приложения.
Определение и свойства сравнений
Определение 1.1. Два целых числа и, дающие при делении на целое положительное число один и тот же остаток называются равноостаточными.
Примеры. 1. Числа 5 и 54 равноостаточные при делении на 7 (в остатке при делении на 7 оба дают 5).
2. Числа -17; 3; 15 равноостаточные при делении на 4.
Теорема 1.2. Для того, чтобы числа и были равноостаточными необходимо и достаточно, чтобы разность делилась на.
Определение 1.3. Целые числа и называются сравнимыми по модулю, если разность делится на.
Обозначение
Читается это так: "сравнимо с по модулю. Сама запись (*) называется сравнением.
Замечания.
Теорема 1.3 утверждает, что определения 1.1 и 1.3 равносильны.
Число, стоящее под знаком будем всегда считать положительным, т. к. сравнение по модулю совпадает со сравнением по модулю.
Если
,
То будем записывать
-
Не сравнимо с по модулю.
Пример. 1.
,
Т. к.
2. , т. к.
Перечислим основные свойства сравнений:
Любое целое число сравнимо с самим собой по любому натуральному модулю.
Если, то
Если и, то
Сравнения по одинаковому модулю можно почленно складывать и вычитать, т. е.
Если и, то
Члены сравнения можно переносить из одной части в другую с противоположным знаком, т. е.
Если, то
К одной части сравнения можно прибавлять или вычитать из нее любое число, кратное модулю, т. е.
Если, то или
Сравнения по одинаковому модулю можно почленно перемножать, т. е.
Если и, то
Обе части сравнения можно возводить в степень с натуральным показателем, т. е.
Если, то
Обе части сравнения можно умножать на одно и тоже целое число, т. е.
Если, то
Обе части сравнения можно делить на их общий делитель, если он взаимно прост с модулем, т. е.
Если и, то
Обе части сравнения и модуль можно умножить на одно и тоже целое положительное число, т. е.
Если то
Обе части сравнения и модуль можно делить на любой их общий делитель, т. е.
Если и, , , то
Если сравнение имеет место по нескольким модулям, то оно имеет место по модулю, равному наименьшему общему кратному данных модулей, т. е.
Сравнение вычет остаток степень плоскость
Если, ,...,, то, где
Если сравнение имеет место по модулю, то оно имеет место и по модулю, равному любому натуральному делителю числа.
Если одна часть сравнения и модуль делятся на какое-нибудь число, то и другая часть сравнения делится на это число.
Задача 1. Показать, что если
, то.
Решение. 1. Воспользовавшись свойством 9 умножим обе части сравнения
На 4, тогда получим следующее сравнение:
2. Заметим, что
, а,
Поэтому ;
Далее: ;
И, наконец, очевидно,
Что
Таким образом, имеем три сравнения:
; ,
3. По свойству сравнений 4, получаем
,
Что и требовалось доказать.
Задача 2.
Выражение
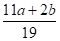
Есть целое число. Доказать, что число
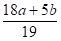
Тоже целое.
Решение. 1. Так как
- целое,
Делится на 19, следовательно
2. Умножим обе части полученного сравнения на 12, получим сравнение
.
3. Очевидно, что
,
Следовательно
И по свойству 9
,
Аналогично можно получить
.
4. По свойству 4,
,
Следовательно по определению сравнимых чисел
Делится на 19, а это и означает, что
Целое число.
Вычеты по данному модулю, системы вычетов
Определение 2.1. Совокупность целых чисел, дающих при делении на натуральное число один и тот же остаток, называется классом вычетов по данному модулю.
Определение 2.2. Вычетом класса вычетов называется любое из чисел, принадлежащих этому классу.
Обозначение
- класс вычетов, порожденный элементом по модулю, где - любое из чисел, дающих при делении на одинаковые остатки.
Пример. Рассмотрим класс вычетов по модулю 3, порожденный числом 11, т. е. . Вычетами этого класса являются, например числа 2; 23;-13;... всего вычетов в классе будет бесконечно много.
Рассмотрим свойства классов вычетов по данному модулю.
Класс вычетов по данному модулю совпадает с множеством чисел вида
,
Где - любое целое число.
Два класса вычетов и совпадают в том и только в том случае, когда
.
Если два класса вычетов и имеют хотя бы один общий элемент, то они совпадают.
Число классов вычетов по конечно и равно ; число вычетов в каждом классе вычетов бесконечно.
Замечания.
- 1. Введение классов вычетов позволяет, таким образом, заменять сравнение равенством соответствующих классов, и наоборот, равенство классов - соответствующим сравнением. 2. Отношение сравнения по данному модулю разбивает все множество целых чисел на непересекающиеся классы вычетов.
Определение 2.3.Полной системой вычетов (ПСВ) по данному модулю называется система чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю.
Замечания.
- 1. Согласно свойству 4, полная система вычетов по состоит из чисел. 2. Обычно в качестве полной системы вычетов употребляется полная система наименьших неотрицательных вычетов по данному модулю, т. е. система чисел: .
Пример. Числа 12; -23; 2; 63;- 2; 5 образуют полную систему вычетов по.
Определение 2.4. Совокупность чисел, взятых из полной системы вычетов и взаимно простых с модулем, называется приведенной системой вычетов по этому модулю.
Задача 3
Показать, что числа 25; -20; 16; 46; -21; 18; 37; -17 составляют полную систему вычетов по модулю.
Решение. 1. По свойству 4, ПСВ, в данном случае, должна состоять равно из 8 чисел, что мы и имеем.
2. В соответствии с определением, так как числа берутся по одному и только по одному из каждого класса вычетов по данному модулю, все числа должны быть не сравнимы по модулю 8, что, по определению 1.3 и теореме 1.2, они должны иметь равные остатки при делении на 8. Найдем остаток от деления каждого из восьми чисел на 8:
; ; ; ; ; ; ; .
Все остатки разные.
Из 1 и 2, на основании определения 2.3 следует, что числа 25; -20; 16; 46; -21; 18; 37; -17 образуют полную систему вычетов по модулю 8
Похожие статьи
-
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера. Определение 3.1. Функцией Эйлера называется функция, определенная на...
-
Анализ - метод научного исследования явлений и процессов, в основе которого лежит изучение составных частей, элементов изучаемой системы. На современном...
-
В современных условиях повышается самостоятельность предприятий в принятии и реализации управленческих решений, их экономическая и юридическая...
-
Математик-циклоп - Великая теорема Ферма
Создание математики -- занятие мучительное и таинственное. Объект доказательства часто бывает ясен, но путь к доказательству теряется в тумане, и...
-
Общие принципы системной организации - Математическое описание объектов управления
Естественно, что решение задач управления, получение законов управления базируется на некоторых формально-математических основах, образующих теорию...
-
Разработка алгоритма нахождения входного потока заявок в имитационной модели контрольно-пропускной системы на основе статистических данных В наши дни...
-
Прагматические свойства информации - Системная революция и принцип дуального управления
Если семантические свойства информации отражают ситуационный аспект существования системы (осмысленность, оформленность ее бытия), то прагматические...
-
Времена - Системная революция и принцип дуального управления
Понятие времени наряду с понятием пространства является наиболее фундаментальным, составляющим основу мировоззрения любого мыслящего существа. В...
-
Общие принципы систематики - Системная революция и принцип дуального управления
Систематика как вполне самостоятельная наука базируется на нескольких основополагающих принципах, выражающих идею системно-физического (системного)...
-
Таблица 1 - Исходные данные для расчета Работа Tminij Tнвij Tmaxij 1-2 15 17 20 1-3 25 28 30 1-4 21 23 25 2-5 14 18 20 2-6 14 17 20 2-7 8 9 10 3-7 25 28...
-
Проводимый предприятиями экономический анализ различается по направлениям, задачам, применяемым методам, объектам изучения и т. д. Классификация анализа...
-
Принцип работы частотного преобразователя. Схема частотного привода - Частотный преобразователь
Переити в каталог продукции: Частотные преобразователи Электроприводы постоянного тока являются очень простыми с точки зрения организации системы...
-
Большинство современных преобразователей частоты построено по схеме двойного преобразования. Они состоят из следующих основных частей: звена постоянного...
-
Постановка задачи применительно для КУП "СПЕЦКОММУНТРАНС": двум погрузчикам разной мощности, это автомобили ТО 28 и ТО 49, за 23 часа нужно погрузить на...
-
Свойства ситуационных пространств - Системная революция и принцип дуального управления
Ситуационные пространства так же материальны, как и существующие в них объекты. В силу этого они оказывают определенное влияние на возникающие в них...
-
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории...
-
Фундаментальные свойства - Системная революция и принцип дуального управления
Существование отношения сходства и различия систем, выделение последних из окружающего мира в виде некоторых устойчивых реалий происходит в результате...
-
Принципы декомпозиционного анализа экономической системы
Принципы декомпозиции Декомпозиция исходной системы или глобальной задачи производится путем применения принципов декомпозиции и координации. Первые...
-
ПРИНЦИПЫ И ПОНЯТИЯ СИСТЕМНО-ФИЗИЧЕСКОГО ПОДХОДА Систематика. Системный анализ и системные исследования Моделирование социально-политических и...
-
Структурная сложность - Системная революция и принцип дуального управления
Сложность реальной системы выражает информационную глубину ее сущности. Разумеется, это свойство, как и любое системное, является относительным. Однако...
-
Морфология процессов - Системная революция и принцип дуального управления
В функциональном (структурно-процессуальном) плане реальная система представляет собой совокупность трех взаимосвязанных функциональных подсистем:...
-
Функциональные свойства систем - Системная революция и принцип дуального управления
Функциональная полнота системы определяет степень соответствия системы функций, выполняемых системой, множеству функций, выполнение которых необходимо с...
-
Евклидовы кольца - Евклидовость в математике
Кольцо целостности Е называется евклидовым, если на множестве Е можно определить функцию е, значение которой является целыми неотрицательными числами,...
-
Организованность. Законы организации - Системная революция и принцип дуального управления
Организованность системы предполагает существование определенных закономерностей и законов построения пространственно-временных форм ее бытия. В...
-
Описание варианта задания - Вероятность безотказной работы
В данной работе необходимо рассчитать вероятность безотказной работы и произвести анализ и оптимизацию полученной по варианту схемы. Для этого...
-
Учения о числе в школе Пифагора - История развития математики
Как известно, Пифагор утверждал, что людей окружают разные предметы. Но все их многообразие не может не иметь под собой единой мировой основы....
-
ПРИНЦИПЫ ИЗМЕРЕНИЙ И ШКАЛИРОВАНИЯ - Многомерный статистический анализ
Измерение шкалирование кластерный регрессионный Измерение - это Присвоение чисел или других символов характеристикам объектов по заранее определенным...
-
Принципы оптимальности в изучении социально-экономических процессов рынка труда
Принципы оптимальности в изучении социально-экономических процессов рынка труда Муравьева Мария Петровна С точки зрения системного анализа рынок труда...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Ответ: В педагогических исследованиях прикладная направленность математики, понимается как содержательная и методическая связь курса математики с...
-
Автоматизированная обработка на ЭВМ позволяет составлять различные сводки, таблицы, ведомости, где информация сгруппирована по каким-либо...
-
Ценности и полезности - Системная революция и принцип дуального управления
Сферы взаимодействия, помимо всего прочего, включают в себя и пространства ценностей, в которых отражаются и оцениваются различные ситуации, возникающие...
-
В данном случае анализируемые системы характеризуются не одним набором показателей эффективности, а несколькими: (18) Где - группа показателей...
-
Рождение проблемы - Великая теорема Ферма
Жизненно важным, поворотным пунктом в развитии западной математики стал 1453 год, когда турки разграбили Константинополь. За прежние годы рукописи,...
-
Упорядочение и классификация объектов с противоречивыми признаками
Упорядочение и классификация объектов с противоречивыми признаками Мультимножество или множество с повторяющимися элементами служит удобной...
-
Опыт проводили в условиях, имитирующих периодическую экстракцию: в стакан одновременно загружали все реагенты и перемешивают их в течение заданного...
-
Общие вопросы Привести объекты судебно-химического (химико-токсикологического) анализа. Дать понятие "вещественным доказательствам". Значение наружного...
-
По ранним и поздним срокам наступления события определяются ранний Tр. н.(i-j) и поздний tп. н.(i-j) сроки начала работы, ранний tр. о.(i-j) и поздний...
-
В данном случае для выбора эффективных решений используется набор принципов оптимальности: (16) В качестве принципов оптимальности выступают принципы:...
-
Факторы - Системная революция и принцип дуального управления
Возникновение системы и ее существование в определенных пространственно-временных масштабах связаны в конечном счете с действием различного рода...
Принцип Дирихле - Разработка контрольных работ по математике