Теоремы Эйлера и Ферма. Нахождение остатков от деления степеней - Разработка контрольных работ по математике
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера.
Определение 3.1. Функцией Эйлера называется функция, определенная на множестве натуральных чисел и равная числу натуральных чисел, не превосходящих и взаимно простых с ним.
Пример. 1.
Действительно числа взаимно простые с числом 10 это числа 1; 3; 7; 9 всего 4.
2. . Действительно, так как число 7 - простое, взаимно простыми с ним являются все натуральные числа меньшие 7: 1; 2; 3; 4;5; 6, всего их 7.
Важным свойством функции Эйлера является ее мультипликативность в случае, когда и числа взаимно простые т. е.
.
Способ вычисления функции Эйлера основан на следующих теоремах:
Теорема 3.2. Пусть простое число, - любое натуральное число, тогда
.
Теорема 3.3. Если
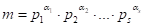
- каноническое разложение натурального числа на простые множители, то
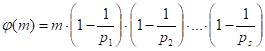
Особую роль в теории сравнений играют теоремы Эйлера и Ферма.
Теорема 3.4. (Эйлера) Для любого модуля и любого взаимно простого с справедливо сравнение:
Теорема 3.5. (Ферма) Если число не делится на простое число, то
Следствие 3.6. При любом целом положительном
.
Теоремы Ферма - Эйлера позволяют часто находить остатки от деления на модуль больших степеней заданного числа. Действительно, если нам надо найти остаток от деления на, где
И,
То можно представить в виде
.
Тогда
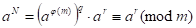
Где может быть значительно меньше, чем.
Задача 4. Найти функцию Эйлера от числа 875.
Решение. 1. Разложим данное число на простые множители
2. По теореме 3.3
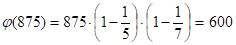
Задача 5. Доказать, что если
, то.
Решение. 1.
;
2. Число 7 - простое, поэтому по теореме Ферма
.
Возведем обе части этого сравнения в квадрат (свойство сравнений 8) и получим верное сравнение:
,
Откуда в соответствии с п.1. следует что
.
Задача 6
Найти остаток от деления на 52.
Решение. 1. Обозначим искомый остаток через
,
Найдем такое число.
2. Вычислим функцию Эйлера от 52:
.
Поделим 2147 на 24 с остатком:
.
3. ,
Таким образом, остаток от деления на 52 равен 7.
Контрольная работа №2 для учащихся 9 классов
Приведенные ниже задания являются контрольной работой №2 для учащихся 9 классов. Каждая задача оценивается в 5 баллов, для зачета нужно набрать не менее 15 баллов.
Правила оформления работ:
Решения по каждому предмету оформляется отдельно. Каждое задание имеет свой шифр (М9.2.1 и т. д.), который указывается перед записью решения. Переписывать текст задачи не надо, достаточно краткой записи, если это необходимо. Оформлять решения в порядке следования заданий. Можно присылать нам столько решений, сколько удалось вам сделать, даже если оказалось невозможным выполнить всю работу.
М 9.2.1. Доказать, что если
, то.
М 9.2.2. Показать, что числа 32; -9; 15; 42; -18; 30; 6 составляют полную систему вычетов по модулю.
М 9.2.3. Показать, что числа 19; 23; 25; -19 составляют приведенную систему вычетов по модулю.
М 9.2.4. Найти функцию Эйлера от числа 1000.
М 9.2.5. Найти остатки от деления
- А) на 7; Б) на 13; В) на 31.
М 9.2.6. Найти две последние цифры следующих чисел 1) ; 2) .
Применение движений плоскости к решению задач элементарной геометрии
Актуальность темы "Преобразования плоскости" очевидна, так как одной из важнейших идей, лежащих в построении курса геометрии, является идея геометрических преобразований, которую обосновал выдающийся немецкий математик Ф. Клейн (1872г.). Групповая точка зрения на геометрию оказала положительное влияние на развитие геометрии, как науки и ее приложения. Групповая точка зрения на геометрические свойства фигур широко используется в физике, химии, биологии, технике. Это сближает математику с данными областями наук. Методы геометрических преобразований позволяют решать большой класс задач элементарной геометрии: задачи на доказательство, построение, вычисление, нахождение геометрических мест точек.
В данной статье мы рассмотрим применение движений - частного случая преобразований плоскости - при решении задач на доказательство. Однако, овладеть этим методом нелегко, поскольку трудно указать какие-либо общие способы использования движений и в большинстве случаев это зависит от конкретной задачи. Суть этого метода состоит в том, что заданную фигуру или ее части подвергают некоторому движению или наряду с заданной фигурой рассматривают ее образ или образы ее частей при этом движении.
В выработке навыков решения помогут рассматриваемые в этой статье образцы решения задач с применением движений.
Как обычно, в конце статьи приводятся задачи для самостоятельного решения, которые составляют контрольную работу по математике для слушателей ХКЗФМШ, обучающихся в 10 классе.
1. Некоторые определения и свойства движений
Определение 1. Взаимно однозначное отображение f плоскости Р на себя называется преобразованием f плоскости Р.
Определение 2. Движением плоскости Р называется такое преобразование f плоскости Р, при котором сохраняется расстояние между двумя любыми точками этой плоскости, т. е.
А, ВР АВ=АВ(1)
Где А= f(А), В=f(В) - образы, соответственно, точек А и В в движении f.
Движения бывают первого и второго рода, при этом движения первого рода не меняют ориентацию фигур, а движения второго рода - меняют ее на противоположную.
Определение 3. Движение h плоскости Р называется произведением (композицией) каких-либо движений f и g этой же плоскости, если оно заключается в последовательном выполнении преобразования f, а затем преобразования g (обозначается: ).
Определение 4. Преобразование плоскости называется тождественным, если оно любую точку плоскости переводит в себя, т. е.
F(A)=A, AP.
Тождественное преобразование обозначается е и удовлетворяет условию:
,
Где f - любое преобразование плоскости Р, в том числе и движение.
Частными видами движений являются осевая симметрия, центральная симметрия, параллельный перенос, вращение (поворот), скользящая симметрия и тождественное преобразование плоскости.
Определение 5. Симметрией относительно прямой (оси симметрии) называется движение плоскости, которое:
Каждую точку прямой преобразует в себя;
Каждую точку А преобразует в точку А такую, что (АА) и середина отрезка АА лежит на. Обозначается осевая симметрия: (рис.1).
Определение 6. Параллельным переносом на вектор называется движение плоскости, которое всякую точку АР преобразует в точку АР такую, что выполняется условие:
(2)
Обозначается параллельный перенос:
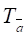
(рис.2)
Определение 7. Вращением (или поворотом) вокруг точки О на угол называется такое преобразование плоскости, при котором:
О О;
Произвольная точка АО переходит в точку А такую, что:
- А) ОА=ОА; Б) АОА = (рис. 3)
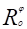
Здесь и далее =АОА означает величину заданного ориентированного угла АОА. Обозначается: .
Определение 8. Симметрией относительно точки О (центр симметрии) называется движение плоскости, которое всякую точку АО преобразует в такую точку А, что точка О является серединой отрезка АА, а точку О преобразует в себя. Обозначается: Z0 (рис. 4)
Заметим, что центральная симметрия Z0 есть поворот Ro на угол 180.
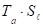
Определение 9. Скользящей симметрией называется произведение осевой симметрии с осью и параллельного переноса на вектор, который параллелен оси : т. е. если l|| , то - скользящая симметрия.
Теорема. Всякое движение I рода есть либо тождественное преобразование, либо параллельный перенос, либо поворот плоскости. Всякое движение II рода есть либо осевая симметрия, либо скользящая симметрия.
Определение 10. Точка называется инвариантной (или неподвижной) точкой преобразования f, если при преобразовании f она отображается на себя.
Прямая называется инвариантной прямой преобразования f, если она отображается на себя.
Если при этом каждая точка прямой остается неподвижной, то прямая называется осью преобразования.
Движения обладают следующими свойствами:
- 1 движение отображает отрезок на отрезок; 2 движение отображает точки, лежащие на одной прямой, в точки, лежащие на одной прямой; 3 движение отображает прямую на прямую, полуплоскость на полуплоскость; 4 движение сохраняет параллельность прямых; 5 движение отображает луч на луч; 6 движение сохраняет величину угла; 7 движение отображает многоугольник на многоугольник со сторонами и углами соответственно той же величины, что и у данного многоугольника; 8 движение отображает окружность на окружность того же радиуса;
Справедлива так же следующая теорема: если АВС и АВС - два треугольника и если АВ=АВ, АС=АС, ВС=ВС, то существует единственное движение плоскости, отображающие точки А, В, С соответственно на точки А, В, С.
Определение 11. Фигура Ф называется равной фигуре Ф (Ф=Ф), если существует движение, при котором фигура Ф преобразуется в фигуру Ф.
2. Примеры решения задач
Задача 1. Обозначим через М - точку пересечения диагоналей равнобедренной трапеции с основаниями АВ и СD а через P и Q - центры окружностей, описанных вокруг треугольников ADM и BCM. Докажите, что:
А) PQ||AB
B) BP = AQ
C) прямая, соединяющая точку М с точками пересечения прямых BP и AQ, делит основания пополам.
Решение. Пусть ось симметрии трапеции - , а P и Q - центры описанных окружностей, соответственно, вокруг треугольников AMD и BCM (рис. 5).
Точка М. Далее
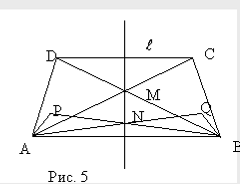
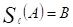
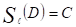
, .
Тогда образом треугольника ADM при осевой симметрии относительно оси будет треугольник ВСМ, т. е.
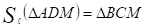
.
Следовательно, образом окружности, описанной вокруг треугольника AMD, при симметрии относительно будет окружность, описанная вокруг треугольника ВСМ. Следовательно,
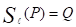
.
Отсюда PQ||AB, BP=AQ. Пусть
,
Тогда N, так как
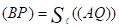
.
Задача 2.
Три равные окружности попарно пересекаются и имеют только одну общую точку D. Доказать, что окружность, проходящая через вторые точки пересечения данных окружностей, равна данным трем окружностям.
Решение. Выполним чертеж, обозначив вторые точки пересечения данных окружностей через А, В, С (рис. 6).
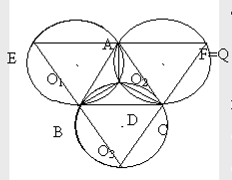
Рассмотрим прямую АD и через точку А проведем прямую, ей перпендикулярную, обозначив точки пересечения этой прямой с окружностями S (O1, R) и S (O2, R) через E и F соответственно. Так как (O1, R) и S (O2, R) симметричны относительно прямой AD, то S(AD)(E)=F, т. е. AD есть серединный перпендикуляр к отрезку EF. Через точку С проведем прямую перпендикулярную CD. Пусть эта прямая пересекает прямую
EF в точке Q, а окружность S(O3, R) - в точке Р.
Так как
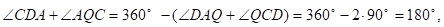
То точка Q лежит на окружности S (O2, R) и, значит, совпадает с точкой F. Аналогично доказанному выше получаем, что перпендикуляр к прямой BD из точки В проходит через точки Е и Р, причем BD является серединным перпендикуляром к отрезку РЕ. Из того, что отрезки АС, ВА и ВС являются средними линиями, очевидно вытекает равенство и, а значит, окружность S (O1, R) равна окружности, проходящей через точки А, В, С, как окружности, описанные около равных треугольников. Что и требовалось доказать.
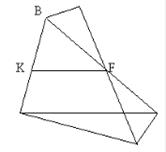
Задача 3
Доказать, что если отрезок KF, соединяющий середины двух противоположных сторон четырехугольника ABCD (K - середина стороны AB, F - середина стороны DC), равен полусумме сторон BC и AD, то четырехугольник есть трапеция (рис.7).
Решение. Выполним параллельный перенос на вектор. Пусть
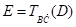
.
Тогда, BF=FE.
Следовательно, линия BFE есть прямая. Тогда KF - средняя линия треугольника ABE:
2KF=AE.
Но по условию 2
KF=AD+BC=AD+DE.
Отсюда следует, что
AE=AD+DE, т. е. DAE. Но DE||BC, тогда и AD||BC.
Задача 4
На сторонах AB и CD параллелограмма ABCD построены квадраты: первый - вне параллелограмма, а второй - по ту же сторону от CD, что и сам параллелограмм. Доказать, что расстояние между центрами квадратов равно ВС.
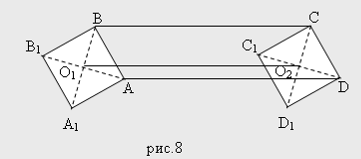
Решение.
Обозначим центры построенных квадратов
и,
Соответственно, через О1 и О2 (Рис. 8). Докажем, что. Выполним параллельный перенос на вектор.
Тогда, т. е. ,
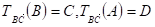
При этом.
Так как,
То
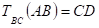
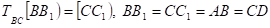
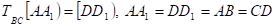
, то.
Следовательно, квадраты
и
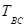
Равны между собой и при параллельном переносе переходят друг в друга, тогда и их центры и также перейдут друг в друга.
Т. е.,
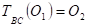
И из определения следует, что
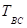
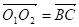
, а значит и.
Задача 5. Дан произвольный треугольник ABC, на сторонах которого построены квадраты. Доказать, что отрезок, соединяющий центры двух квадратов, построенных на сторонах АВ и ВС, равен и перпендикулярен отрезку, соединяющему точку В с центром третьего квадрата.
Решение. Выполним чертеж (рис.9) и рассмотрим поворот вокруг точки А на угол, равный. Из условия задачи очевидно, что
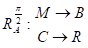
,
А образом точки Р будет некоторая точка F. При этом имеем, что
и.
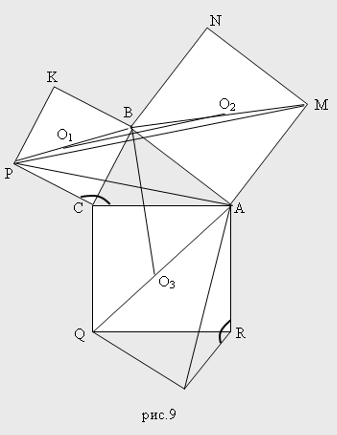
Из равенства треугольников АСР и ARF вытекает
,
Но тогда будут равны и углы АСВ и QRF. Рассматривая центральную симметрию, легко убедиться, что
,
Так как эта симметрия точку С переводит в R, луч СВ - в луч RF и
.
Из того, что
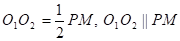
и
Является серединой BF, с учетом соотношений
и
Сразу получаем равенство и перпендикулярность отрезков и. Утверждение задачи доказано.
Задача 6. Дан равносторонний треугольник АВС и произвольная точка М. Доказать, что больший из трех отрезков MA, МВ и МС не больше суммы двух других отрезков. В каком случае больший из отрезков MA, МВ и МС будет равен сумме двух других?
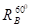
Решение. Пусть ВМ - наибольший из указанных отрезков (рис.10). Выполним поворот плоскости вокруг точки В на 600.
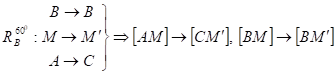
Треугольник - равносторонний. Поэтому
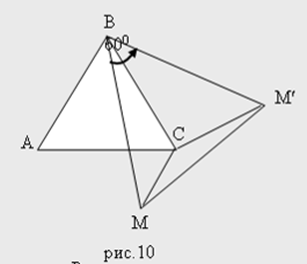
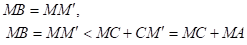
.
Равенство будет в том и только в том случае, если точка М лежит на окружности, описанной вокруг треугольника АВС.
Задача 7
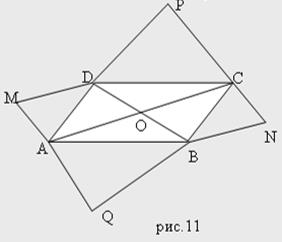
На сторонах параллелограмма ABCD вне его построены правильные треугольники ABQ, BCN, CDP и DAM. Доказать, что отрезки PQ и MN имеют общую середину.
Решение.
Выполним чертеж (рис.11) и рассмотрим центральную симметрию с центром в точке О - точке пересечения диагоналей параллелограмма. Очевидно, что
.
А это означает, что О является общей серединой отрезков PQ и MN, что и утверждалось в условии задачи.
Похожие статьи
-
Принцип Дирихле - Разработка контрольных работ по математике
В математике большое значение имеют так называемые доказательства существования. Самый простой способ доказать существование объекта с заданными...
-
Теоремы Ферма, Ролля, Лагранжа и Коши
Введение В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи...
-
Рождение проблемы - Великая теорема Ферма
Жизненно важным, поворотным пунктом в развитии западной математики стал 1453 год, когда турки разграбили Константинополь. За прежние годы рукописи,...
-
Математик-циклоп - Великая теорема Ферма
Создание математики -- занятие мучительное и таинственное. Объект доказательства часто бывает ясен, но путь к доказательству теряется в тумане, и...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
"Доказана ли Великая теорема Ферма?" - Великая теорема Ферма
Был сделан лишь первый шаг на пути к доказательству гипотезы Таниямы-Шимуры, но избранная Уайлсом стратегия была блестящим математическим прорывом,...
-
Позор математики - Великая теорема Ферма
С тех пор, как я еще мальчиком впервые столкнулся с Великой теоремой Ферма, она стала моим увлечением на всю жизнь, -- вспоминает Эндрю Уайлс, и его...
-
Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий,...
-
Векторы, и образуют правую тройку векторов. - Сферический треугольник и его применение
Свойства: 1. 2. 3. 4. 13. Смешанное произведение векторов и его свойства . Смысл смешенного произведения: сначала два вектора векторно перемножают, а...
-
Q(x) - соответствует площади боковой поверхности данного тела от точки А до точки х. Q(x)>х€[a, x]. Q (x+?x)>х€[a, x+?x], тогда ?Q=Q...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Запечатанные конверты - Великая теорема Ферма
После прогресса, достигнутого благодаря работам Софи Жермен, Французская Академия Наук установила серию премий, включая золотую медаль и 3000 франков,...
-
Месье Леблан - Великая теорема Ферма
К началу XIX века за Великой теоремой Ферма установилась устойчивая репутация самой трудной проблемы в теории чисел. После прорыва, осуществленного...
-
Доказательство теоремы Ферма Уважаемый Григорий Яковлевич! Обращается к Вам Черепанов Николай Михайлович, математик из Барнаула. В 2004 году, я...
-
Введение, История теоремы - Великая теорема Ферма
Она заинтересовала меня тем, что на вид очень простая и казалось бы, решить ее может каждый школьник, но найти ее решение на протяжении 358 лет пытались...
-
Эра загадок и головоломок - Великая теорема Ферма
С античных времен и поныне математики пытались придать занимательность своим учебникам, излагая теоремы и доказательства в форме решений числовых...
-
Ответ: y=f(kx) получается из Графика функции f(x) сжатием его вдоль оси ох в k раз, если k>1 и растяжением в 1 деленную на k раз, если k>0 но меньше 1....
-
Уход в абстракцию - Великая теорема Ферма
После работ Эрнста Куммера надежды найти доказательство ослабли, как никогда прежде. Кроме того, в математике начали развиваться различные новые области....
-
Свойство 1. Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания...
-
Разработка алгоритма нахождения входного потока заявок в имитационной модели контрольно-пропускной системы на основе статистических данных В наши дни...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ - Основы моделирования геометрических объектов
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических...
-
Некоторые векторные равенства Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные...
-
Симплекс - метод - Интегральное и дифференциальное исчисление
Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
-
Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
Теорема Пенлеве - Условия Фукса и теорема Пенлеве
Все приведенные выше исследования велись в предположении, что мы изучаем поведение интеграла в области изменения z, при котором w(z) принимает вполне...
-
Учения о числе в школе Пифагора - История развития математики
Как известно, Пифагор утверждал, что людей окружают разные предметы. Но все их многообразие не может не иметь под собой единой мировой основы....
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
-
Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...
-
Интегральная теорема Муавра-Лапласа
Предположим, что в условиях схемы Бернулли проводится испытаний, в результате каждого из которых с вероятностью () происходит событие. Интегральная...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
После семи лет работы в одиночку Уайлс наконец завершил доказательство гипотезы Таниямы-Шимуры и считал, что его мечта -- доказать Великую теорему Ферма...
-
В потемках - Великая теорема Ферма
Уайлс, о котором мир тогда еще ничего не знал, с облегчением вздохнул. Великая теорема Ферма по-прежнему оставалась непобежденной, и он мог продолжать...
-
Дуэль с бесконечностью - Великая теорема Ферма
Чтобы доказать Великую теорему Ферма, Уайлсу было необходимо сначала доказать гипотезу Таниямы-Шимуры о том, что каждой эллиптической кривой можно...
-
Снова великая теорема Ферма! - Великая теорема Ферма
Сегодня в доказательстве великой теоремы Ферма произошел поистине поразительный сдвиг. Наум Элькис (профессор Гарвардского университета) заявил, что...
-
Эндрю Уайлс во время обучения в колледже. Тайные вычисления - Великая теорема Ферма
"Однажды вечером, в конце лета 1986 года, я попивал чай в гостях у своего приятеля. В беседе он между прочим упомянул о том, что Кену Рибету удалось...
Теоремы Эйлера и Ферма. Нахождение остатков от деления степеней - Разработка контрольных работ по математике