Свертка скалярных критериев и условия компромисса - Моделирование распределительных процессов на основе динамических задач векторной оптимизации
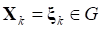
Пусть ограничения (4) не противоречивы, т. е. не пусто множество допустимых решений, а оптимальное решение достигается я в точке для каждой K-ой скалярной задачи (3) (4), т. е.
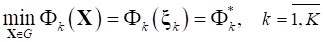
, (6)
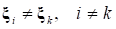
Причем очевидно, что в общем должно выполняться условие.
Основываясь на методологии "идеальной точки", инкапсулированной в свертке скалярных компонент вектора критериев (3), преобразуем многокритериальную задачу (3),(4) к параметрической оптимизации обобщенной задачи математического программирования [8, 9].
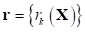
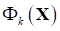
На первом этапе ее анализа введем вектор невязок, с компонентами, характеризующими не достижимость оптимума каждого отдельного критерия в каждой точке области допустимых решений, следующим образом:
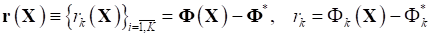
(7)
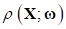
В указанных обозначениях преобразуем векторную задачу (3),(4) к эквивалентной задаче минимизации среднеквадратичной свертки взвешенных невязок
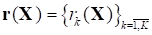
,
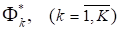
как отклонений от - соответствующих локальных оптимумов (6).
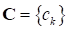
Обозначая через весовой вектор, окончательно агрегированную однокритериальную задачу представим в виде:
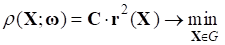
(8)
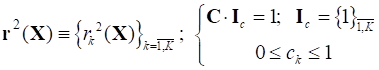
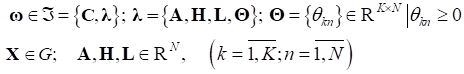
Область допустимых решений G в (8) определена условиями (4).
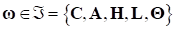
Таким образом, показано, что исходная динамическая многокритериальная задача (3) при выполнении ограничений (4) эквивалентна порожденной задаче параметрической оптимизации (8) на множестве параметров-векторов и условий ограничений (4).
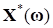
Последующий анализ (8) реализуется в два этапа. Вначале определяется параметрическое множество оптимальных решений задачи условной оптимизации (8) [1, 6], таких что:
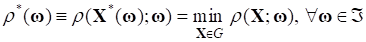
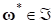
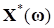
Затем формулируется условие параметрического компромисса, на основе которого определяется оптимальное значение параметра. Такое решения параметрической задачи минимизации агрегированной целевой функции, описывающей общие потери и инкапсулирующей невязки, характеризующие для каждого значения параметра "неоптимальность" каждого отдельного критерия на параметрическом множестве точке, предложено в виде:
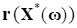
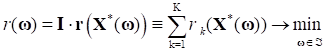
(10)
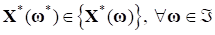
Такой результат оптимизации соотношения (10) задает параметрическое оптимальное решение исходной многокритериальной задачи, количественно выражая понимание оптимального межкритериального компромисса.
Следует заметить, что в большинстве прикладных задач параметрический вектор, определенный в (8), детерминирован исходя из экономических, технологических или бизнес условий функционирования распределительных систем. В связи с этим, целесообразно проблему поиска (10) представить как частную задачу оптимальной параметризации свертки скалярных критериев относительно их весового вектора С, т. е.:
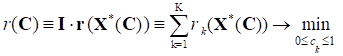
(11)
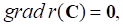
В случае непрерывной зависимости искомое оптимальное цможно устанавить на основе необходимых условий экстремума в скалярной форме принимающих вид:
Похожие статьи
-
Для примера рассмотрим вытекающую из общей постановки (3),(4) двухкритериальную () многоэтапную динамическую задачу, с целевыми функциями дохода и потерь...
-
Развитие методов многокритериальной оптимизации сложных систем обусловлено необходимостью повышения эффективности их функционирования на основе обобщения...
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
1. Золотарев А. А. Математическое моделирование и оптимизация распределительных систем. Saarbrucken: LAP Lambert Academic Publishing, 2016. 184 с. 2....
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории...
-
Критерии оптимальности в задачах с ограничениями - Линейное программирование в экономике
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно...
-
К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло,...
-
Изучив основные вопросы, связанные с календарным планированием, подведем итог. Задачи календарного планирования отражают процесс распределения во времени...
-
ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ - Основы моделирования геометрических объектов
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических...
-
В этом случае лучшим считается вариант, у которого суммарная величина отдельных целевых функций принимает максимальное значение: F Max = = max...
-
Задание. Рассматривается вычислительная система состоящая из n вычислительных машин. Имеется n задач. Задана матрица T определяющая время решения i-й...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые...
-
Задача маршрутизации реализуется набором алгоритмов, каждый из которых осуществляет решение задачи коммивояжера. Коммивояжер (распространитель товаров)...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Оптимизация инвестиционного портфеля (ИП) [Дубровин и др., 2008], [Мищенко и др., 2002], [Серов, 2000] является одной из важных экономических задач,...
-
Программное управление Относительно просто может быть сформулирована так называемая задача программного управления. В ней предполагается, что управляющие...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Геометрическая интерпретация - Математические методы и модели в экономике
Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...
-
Обычно субъект экономической жизни стремится достичь сразу многих целей. Например, он стремится одновременно следовать и внутренним, и внешним целям, тем...
-
Задача Джонсона о двух станках Рассмотрим задачу последовательной обработки на двух машинах N различных деталей, если известно время Ai и Bi обработки...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Как и каждый достаточно ярко выраженный класс экономико-математических моделей, совокупность моделей календарного планирования обладает рядом...
-
Как известно, человечество в своем стремительном развитии старается все более расширить сферы своей деятельности, сталкиваясь при этом с множеством новых...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Оптимальное решение модели. - Методика решения задачи целочисленного программирования
Рис. 1 Шаг 1. Исходную задачу 1 заносим в дерево задач. В качестве исходного допустимого решения берем: x1=x2=x3=0. Соответствующее значение целевой...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Важнейшие математические модели обычно обладают важным свойством Универсальности : принципиально разные реальные явления могут описываться одной и той же...
-
Основные задачи анализа временных рядов. Базисная цель статистического анализа временного ряда заключается в том, чтобы по имеющейся траектории этого...
-
Математическое моделирование экономических явлений и процессов является, как указывалось выше, важным инструментом экономического анализа. Оно позволяет...
-
Математическое моделирование - Основы научных исследований
Выше уже указывалось, что Математическое моделирование - это получение решений уравнений, составляющих математическую модель объекта, при изменении...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Аппроксимация функции предпочтения ЛПР нейронными сетями имеет в работе ту особенность, что процесс обучения нейронных сетей происходит в условиях малой...
Свертка скалярных критериев и условия компромисса - Моделирование распределительных процессов на основе динамических задач векторной оптимизации