Количественный анализ и параметрическая оптимизация - Моделирование распределительных процессов на основе динамических задач векторной оптимизации
Для примера рассмотрим вытекающую из общей постановки (3),(4) двухкритериальную () многоэтапную динамическую задачу, с целевыми функциями дохода
и потерь
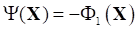
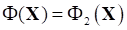
,
Связанных с отклонениями этапных объемов выпуска продукции от плана (портфеля заказов), т. е.
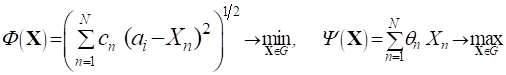
(11)
Тогда на основании (9), обозначая
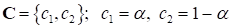
(где - параметр взвешивания), агрегированная свертка скалярных критериев (11) принимает вид
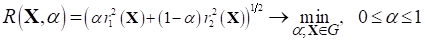
(12)
;
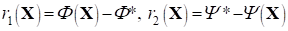
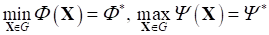
Численный эксперимент позволил выделить закономерности оптимальной параметризации критериальной свертки (12) на основе реализации детерминированных методов и эвристических алгоритмов оптимизации (Particle Swarm Optimization, Нелдера-Мида) [10 - 11].
Характерное поведение параметрической зависимости функции "потерь" представлено на рис. 1 для двухэтапной задачи. Здесь, соответствующее условию (10) минимизации потерь [12]
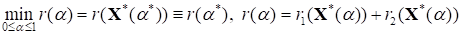
,
Оптимальное по параметру решение X*=X*(*) отмечено как точка X* на параметрической траектории оптимальных решений X*() критериальной свертки (12).
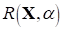
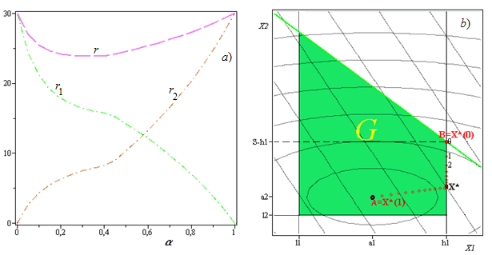
Рис. 1 - Параметрическая зависимость потерь и оптимальных X*()
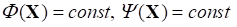
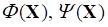
На рис. 1 сеткой сплошных линий отображены два семейства изолиний целевых функций (11) в виде выпуклых и прямых линий, соответственно. На плоскости X1OX2 пронумерованы точки {I=0,1,2,...} параметрической последовательности X*(I) для дискретных изменений I=Ih с шагом H=0,05 (0?I?1). Причем, соответствующие =0 и =1 крайние точки такой последовательности, обозначенные как B и A, являются оптимальными для каждого отдельного критерия, где реализуются их оптимумы.
Соответствующие значения исходных данных и выявленного оптимального решения приведены в таблице.
Таблица
Исходные данные и параметрически оптимальное решение X*
|
I |
Ci |
I |
Ai |
Li |
Hi |
S |
* |
R( *) |
X*(X1*,X2*) |
|
1 |
1/4 |
2/3 |
40 |
10 |
70 |
120 |
0,32 |
23.844 |
70 |
|
2 |
3/4 |
1/3 |
20 |
10 |
150 |
27,183 |
Видно, что кривая валовых потерь при =* имеет явно выраженный минимум (параметрический оптимум), который достигается в граничной точке регуляризация планирование однопродуктовый
X*=X*(*)
Области G, являющейся точкой излома кусочно-линейной траектории оптимальных X*(I) задачи (12).
Моделирование в широком диапазоне входных параметров и оптимизация режимов функционирования рассматриваемых динамических систем на основе предложенной параметрической минимизации зависимости суммарных потерь в случаях более высоких размерностей задач выявили аналогичные закономерности.
Работа выполнена в рамках научного проекта РФФИ №13-01-00943
Похожие статьи
-
Пусть ограничения (4) не противоречивы, т. е. не пусто множество допустимых решений, а оптимальное решение достигается я в точке для каждой K -ой...
-
Развитие методов многокритериальной оптимизации сложных систем обусловлено необходимостью повышения эффективности их функционирования на основе обобщения...
-
1. Золотарев А. А. Математическое моделирование и оптимизация распределительных систем. Saarbrucken: LAP Lambert Academic Publishing, 2016. 184 с. 2....
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
Основные задачи анализа временных рядов - Динамические ряды
Принципиальные отличия временного ряда от последовательности наблюдений, образующих случайную выборку, заключаются в следующем: Во-первых, в отличие от...
-
ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ - Основы моделирования геометрических объектов
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических...
-
Основные задачи анализа временных рядов. Базисная цель статистического анализа временного ряда заключается в том, чтобы по имеющейся траектории этого...
-
Постановка задачи регрессионного анализа - Основы научных исследований
Основное назначение Регрессионного анализа (РА) - получение по экспериментальным данным зависимостей, аппроксимирующих эти данные в виде алгебраических...
-
Изучив основные вопросы, связанные с календарным планированием, подведем итог. Задачи календарного планирования отражают процесс распределения во времени...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Параметрическое линейное программирование - Методы линейного программирования
Представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или...
-
С целью формализации задачи введем необходимые обозначения: I - код изделия (i = 1,...,n); ХI - искомый объем выпуска годовой программы по i-му изделию;...
-
В качестве примера конкретной модели процесса управления обсудим модель распределения времени между овладением знаниями и развитием умений, впервые...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Процесс экономико-математического моделирования - Экономико-математические методы
Этот процесс состоит из нескольких взаимосвязанных этапов. Разбиение на этапы и выделение на каждом этапе присущих ему процессов условно: на одном из...
-
Программное управление Относительно просто может быть сформулирована так называемая задача программного управления. В ней предполагается, что управляющие...
-
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ - Основы моделирования геометрических объектов
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные...
-
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная,...
-
В результате проведенного финансового анализа предприятия можно сделать вывод, что состояние его удовлетворительное, но имеется ряд недостатков: В...
-
ПРИНЦИПЫ И ПОНЯТИЯ СИСТЕМНО-ФИЗИЧЕСКОГО ПОДХОДА Систематика. Системный анализ и системные исследования Моделирование социально-политических и...
-
Задание. Рассматривается вычислительная система состоящая из n вычислительных машин. Имеется n задач. Задана матрица T определяющая время решения i-й...
-
Моделирование системы в условиях неопределенности - Основы теории систем и системного анализа
Как уже отмечалось в первой части нашего курса, в большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий...
-
Программное управление является приемлемым подходом во многих прикладных ситуациях. На этом принципе основаны, например, простые металлорежущие станки...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло,...
-
Как известно, человечество в своем стремительном развитии старается все более расширить сферы своей деятельности, сталкиваясь при этом с множеством новых...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Описание процесса решения - Формирование оптимального штата фирмы
На рабочем листе Excel в диапазоне ячеек от А1 до D4 в зависимости от выбранного количества предприятий размещаются исходные данные. Они будут...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Этапы моделирования - Общая схема и этапы процесса экономико-математического моделирования
Проанализируем последовательность и содержание этапов одного цикла экономико-математического моделирования. 1. Постановка экономической проблемы и ее...
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...
-
Пример успешного использования методов многошагового обучения для задачи управления производством. Рассмотрим простейший вариант, когда производится лишь...
Количественный анализ и параметрическая оптимизация - Моделирование распределительных процессов на основе динамических задач векторной оптимизации