Разложение правильной рациональной дроби на сумму простейших дробей. - Методы решения системы линейных уравнений

Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде всего знаменатель Q(x) записывают в виде произведения сомножителей, каждый из которых является либо степенью линейной функции x-a, либо степенью квадратичной функции x2+px+q, которая не имеет действительных корней.

Каждому сомножителю (x-a)K разложения Q(x) отвечает в разложении дроби P(x)/Q(x) выражение вида A1/(x-a)+A2/(x-a)2+...+AK/(x-a)K (1).

А каждому сомножителю (x2+px+q)L - выражение вида (B1X+C1)/(x2+px+q)+(B2X+C2)/(x2+px+q)2+...+ (BLX+CL)/(x2+px+q)L (2).

Отсюда вытекает следующее практическое правило разложения правильной рациональной дроби на простейшие множители:

A. Разложить знаменатель Q(x) на линейные и квадратичные множители, не имеющие действительных корней.

B. Записать разложение данной рациональной дроби P(x)/Q(x) на простейшие дроби с неопределенными (буквенными) коэффициентами, используя выражения вида (1) и (2).

C. Полученное равенство умножить на общий знаменатель.

D. Раскрыть скобки, привести подобные члены и приравнять коэффициенты при одинаковых степенях х.

E. Решить полученную систему линейных уравнений относительно искомых коэффициентов.

Определенный интеграл

Пусть функция f(x) определена на отрезке a?x?b. Разобьем этот отрезок на n частей точками a = x0<x1<x2<...<xN = b, выберем на каждом элементарном отрезке xK-1?x?xK произвольную точку оK и обозначим ДxK длину каждого такого отрезка. Интегральной суммой для функции f(x) на отрезке a?x?b, называется сумма вида

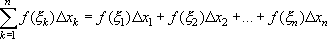
Определенным интегралом от функции f(x) на отрезке a?x?b называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

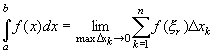
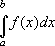
Для любой функции f(x), непрерывной на отрезке a?x?b, всегда существует определенный интеграл.

Для вычисления определенного интеграла от функции f(x) в том случае, когда можно найти соответствующий неопределенный интеграл F(x), служит формула Ньютона-Лейбница:

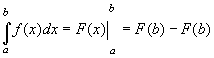
Т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

1. Определенный интеграл от суммы или разности конечного числа функций равен сумме или разности определенных интегралов от этих функций. 2. Постоянный множитель можно выносить за знак определенного интеграла. 3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный. 4. Определенный интеграл с одинаковыми пределами равен нулю. 5. Отрезок интегрирования можно разбивать на части.

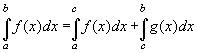
При вычислении определенного интеграла методом замены переменный (способом подстановки) определенный интеграл, преобразуется с помощью подстановки u = ш(x) и x = ц в определенный интеграл относительно новой переменной u. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами интегрирования б и в, которые находятся из исходной подстановки. Из первой подстановки новые пределы интегрирования вычисляются непосредственно б = ш(a), в = ш(b).

Из второй подстановки новые пределы интегрирования находятся путем решения уравнения a = ц(б) и b = ц(в) относительно б и в.

Таким образом, имеем

Похожие статьи

• Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений

  Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...

• Производной. - Методы решения системы линейных уравнений

  Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...

• Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений

  Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...

• Счетные и несчетные множества - Методы решения системы линейных уравнений

  Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...

• Элементы матричного анализа - Методы решения системы линейных уравнений

  Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...

• Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений

  1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...

• Свойства операции умножения матриц - Методы решения системы линейных уравнений

  1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...

• Функции и ее свойства - Методы решения системы линейных уравнений

  В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...

• Частные производные высших порядков - Методы решения системы линейных уравнений

  Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...

• Матрицы и определители - Методы решения системы линейных уравнений

  Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...

• Алгебраические дополнения, Обратная матрица, войства обратных матриц. - Методы решения системы линейных уравнений

  Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...

• Системы линейных уравнений - Методы решения системы линейных уравнений

  Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...

• Ранг матрицы. - Методы решения системы линейных уравнений

  Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...

• Понятие рациональной дроби, Интегрирование рациональных дробей - Неопределенный интеграл

  Пусть даны два многочлена РN(х)=aNXN+aN-1XN+1+ ... +a1X1+a0 и QM(x)= bMXM+bM-1XM+1+ ... +b1X1+b0 (aN, bM?0). О: Функция R(х) называется...

• Автоматизированное решение транспортной задачи линейного программирования, Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала., С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции. - Определение оптимальной стратегии рыночного поведения с использованием макроэкономических методов и моделей

  В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....

• Определение определенного интеграла - Определенный интеграл

  Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение...

• Обобщенные интервальные оценки исходных данных - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...

• Базовые понятия экономики, используемые в проекте - Применение решения систем линейных уравнений с двумя неизвестными для решения задач рыночной экономики

  Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....

• Принципы построения программ с автоматическим выбором шага, Решение задачи, Блок-схема программы, Результаты решения - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага

  При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...

• Уравнение линии на плоскости - Методы решения системы линейных уравнений

  Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...

• Теоремы о пределах, По &;nbsp;теореме&;nbsp; о связи &;nbsp;предела&;nbsp; и бесконечно малой функции: - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...

• Действия над комплексными числами в алгебраической форме, Четность и нечетность функции, Монотонность и периодичность функции, Предел функции в точке - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...

• Элементарные преобразования, Миноры - Методы решения системы линейных уравнений

  Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...

• Определители (детерминанты) - Методы решения системы линейных уравнений

  Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...

• РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера

  Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...

• О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...

• Анализ чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции., Графический способ анализа чувствительности оптимального решения к вариациям C[j - Исследование чувствительности оптимального решения задачи линейного программирования к вариациям ее параметров и введению нового ограничения

  Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...

• Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике

  Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...

• Анализ работы методов - Комплексное исследование численных методов для задачи решения нелинейных уравнений

  Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...

• Теоремы двойственности и их использование в задачах ЛП - Решение оптимизационных экономических задач методами линейного программирования

  Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....

• Геометрический смысл определенного интеграла - Неопределенный интеграл

  О: Площадь криволинейной трапеции равна определенному интегралу, вычисленному от функции, график которой является верхним основанием, а ось абсцисс -...

• Функции распределения вероятностей для параметров, описываемых обобщенными интервальными оценками - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...

• Особенности постановки и решения общей задачи линейного программирования - Определение оптимальной стратегии рыночного поведения с использованием макроэкономических методов и моделей

  Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....

• Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...

• Закон спроса, Закон предложения - Применение решения систем линейных уравнений с двумя неизвестными для решения задач рыночной экономики

  При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...

• Паспорт проектной деятельности - Применение решения систем линейных уравнений с двумя неизвестными для решения задач рыночной экономики

  1. Название проекта: "Математические модели в экономике". 2. Руководитель: учитель математики Тыкоцкая Л. И. 3. Учебные предметы: математика, экономика....

• Применение решения систем линейных уравнений с двумя неизвестными для решения задач рыночной экономики

  По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...

• Обоснование проекта - Применение решения систем линейных уравнений с двумя неизвестными для решения задач рыночной экономики

  Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...

• Изложение теоретических аспектов исследования, Динамическое программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

  Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...

• Различные способы формализации экономико-математических и технических систем - Применение экономико-математических методов и моделей в управлении производством (на примере КУП "Спецкоммунтранс")

  Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...

Разложение правильной рациональной дроби на сумму простейших дробей. - Методы решения системы линейных уравнений

Предыдущая | Следующая