Теоремы Ферма, Ролля, Лагранжа и Коши
Введение
В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи рассуждения, доказательства".
В тексте реферата раскрываются понятия функции и дифференцируемость функции, пределы и непрерывность функции в точке.
Общее понятие "функция" претерпело длительную и довольно сложную эволюцию. Термин "функция" впервые появилась в 1692г. у Г. Лейбница, в некотором более узком смысле. В смысле, близком к современному, этот термин употребил в письме к Лейбницу в 1698г. швейцарский ученый И. Бернулли.
В формировании современного понимания функциональной зависимости приняли участие многие крупные математики.
В аппарате изучения различных свойств функции особое место занимает теорема Лагранжа, благодаря этой теореме можно установить условия постоянства и монотонности функции. Также в теоремах Лагранжа доказываются достаточные условия экстремума.
Не менее знаменитый математик Ферма Пьер, один из создателей аналитической геометрии и дифференциального исчисления. Открыл правило нахождения экстремума с помощью производной. Автор многих теорем теории чисел. Знаменитая теорема Ферма из теории чисел, которую Ферма сформулировал без доказательства, не доказана до сих пор. Формулировка Ферма гласит: "Разделить куб на два других куба и вообще какую-нибудь степень выше второй на две степени с тем же обозначением невозможно, и я нашел воистину замечательное доказательство этого, но поля слишком узки, чтобы вместить его" .
Большой вклад в математику также внес Коши. Его определение предела функции является эквивалентным и по Гейне и доказывается одной теоремой.
Но дается два определения предела функции (по Коши, по Гейне). Общее понятие предела функции выглядит так: "Число b называется пределом функции f в точке а (или: при стремящемся к а, при а) и пишут
Lim f (v) =b,
А
Если для любого положительного числа можно подобрать такое положительное число, что
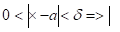
F(
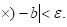
Теорема Ролля является частным случаем теоремы Лагранжа, когда
F (а)-f(b) т. е. когда секущая AB параллельна оси ОЖ. И рассматривается там подробно.
1. Теорема Коши
Функция экстремум теорема коши
Предел и непрерывность функции в точке. Эквивалентность различных определений предела функции.
Пусть функция y =f(х) определена на некотором бесконечном множестве Х и пусть R - предельная точка множества Х. (т. е. любая окрестность этой точки содержит бесконечно много точек множества Х, при этом сама точка может и не принадлежать множеству).
Обозначим:
Дадим два определения предела функции.
1. Определение предела функции по Коши.
Число b называется пределом функции y= f(х) в точке, если для любой - окрестности точки b найдется - окрестность точки, такая, что для всех из области определения функции, содержащихся в проколотой - окрестности точки, соответствующие значения функции f(x) содержатся в - окрестности точки b.
( и b могут быть как конечными, так и бесконечными).
В частности, если и b конечные, определение можно переформулировать следующим образом:
Если же, = а b - конечное, то:
Lim f (x)=b>0 ?
Аналогично определяются остальные случаи.
2. Определение предела функции по Гейне.
Число b называется пределом функции y = f(x) в точке, если для любой последовательности значений аргумента x
Похожие статьи
-
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера. Определение 3.1. Функцией Эйлера называется функция, определенная на...
-
Месье Леблан - Великая теорема Ферма
К началу XIX века за Великой теоремой Ферма установилась устойчивая репутация самой трудной проблемы в теории чисел. После прорыва, осуществленного...
-
Запечатанные конверты - Великая теорема Ферма
После прогресса, достигнутого благодаря работам Софи Жермен, Французская Академия Наук установила серию премий, включая золотую медаль и 3000 франков,...
-
Математик-циклоп - Великая теорема Ферма
Создание математики -- занятие мучительное и таинственное. Объект доказательства часто бывает ясен, но путь к доказательству теряется в тумане, и...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Рождение проблемы - Великая теорема Ферма
Жизненно важным, поворотным пунктом в развитии западной математики стал 1453 год, когда турки разграбили Константинополь. За прежние годы рукописи,...
-
Уход в абстракцию - Великая теорема Ферма
После работ Эрнста Куммера надежды найти доказательство ослабли, как никогда прежде. Кроме того, в математике начали развиваться различные новые области....
-
Дуэль с бесконечностью - Великая теорема Ферма
Чтобы доказать Великую теорему Ферма, Уайлсу было необходимо сначала доказать гипотезу Таниямы-Шимуры о том, что каждой эллиптической кривой можно...
-
Эндрю Уайлс во время обучения в колледже. Тайные вычисления - Великая теорема Ферма
"Однажды вечером, в конце лета 1986 года, я попивал чай в гостях у своего приятеля. В беседе он между прочим упомянул о том, что Кену Рибету удалось...
-
Эра загадок и головоломок - Великая теорема Ферма
С античных времен и поныне математики пытались придать занимательность своим учебникам, излагая теоремы и доказательства в форме решений числовых...
-
Награда Эндрю - Великая теорема Ферма
Предложенное Уайлсом доказательство Великой теоремы Ферма опирается на доказательство гипотезы, родившейся в 50-е годы XX века. Его рассуждения...
-
Доказательство теоремы Ферма Уважаемый Григорий Яковлевич! Обращается к Вам Черепанов Николай Михайлович, математик из Барнаула. В 2004 году, я...
-
"Доказана ли Великая теорема Ферма?" - Великая теорема Ферма
Был сделан лишь первый шаг на пути к доказательству гипотезы Таниямы-Шимуры, но избранная Уайлсом стратегия была блестящим математическим прорывом,...
-
Введение, История теоремы - Великая теорема Ферма
Она заинтересовала меня тем, что на вид очень простая и казалось бы, решить ее может каждый школьник, но найти ее решение на протяжении 358 лет пытались...
-
Создатель Великой проблемы - Великая теорема Ферма
Пьер де Ферма родился 20 августа 1601 года в городе Бомон-де-Ломань на юго-западе Франции. Его отец, Доминик Ферма, был состоятельным торговцем кожей,...
-
Аспирантские годы - Великая теорема Ферма
В 1975 году Эндрю Уайлс поступил в аспирантуру Кембриджского университета. В ближайшие три года ему предстояло работать над диссертацией на соискание...
-
Позор математики - Великая теорема Ферма
С тех пор, как я еще мальчиком впервые столкнулся с Великой теоремой Ферма, она стала моим увлечением на всю жизнь, -- вспоминает Эндрю Уайлс, и его...
-
Снова великая теорема Ферма! - Великая теорема Ферма
Сегодня в доказательстве великой теоремы Ферма произошел поистине поразительный сдвиг. Наум Элькис (профессор Гарвардского университета) заявил, что...
-
После семи лет работы в одиночку Уайлс наконец завершил доказательство гипотезы Таниямы-Шимуры и считал, что его мечта -- доказать Великую теорему Ферма...
-
"Ферматисты" - Великая теорема Ферма
Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о...
-
Доказательство теоремы ошибочно - Великая теорема Ферма
Едва Уайлс закончил свою лекцию в Кембридже, как комиссию Вольфскеля известили о том, что Великая теорема Ферма, наконец, доказана. Премия не могла быть...
-
Теорема Ферма в творчестве - Великая теорема Ферма
В телесериале "Звездный Путь", капитан космического корабля Энтерпрайз NCC-1701-D Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма во второй...
-
В потемках - Великая теорема Ферма
Уайлс, о котором мир тогда еще ничего не знал, с облегчением вздохнул. Великая теорема Ферма по-прежнему оставалась непобежденной, и он мог продолжать...
-
Метод множителей Лагранжа - Экономико-математические методы
Среди задач (4.1)-(4.3) особое место занимают задачи типа (6.10) , (6.11) Для решения которых можно воспользоваться классическим методом оптимизации...
-
Теорема Ферма - Математичний аналіз
Якщо ф-я диф. в деякому околі Т. х0 і досягає в ній екстремума, то похідна = 0. Доведення: Нехай ф. досягає в екстремума в т. х0, тоді існує окіл т. х0,...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Метод Колывагина-Флаха - Великая теорема Ферма
К лету 1991 года Уайлс проиграл сражение: теорию Ивасавы не удалось приспособить к решению проблемы. Он снова обратился к научным журналам и монографиям,...
-
Интегральная теорема Муавра-Лапласа
Предположим, что в условиях схемы Бернулли проводится испытаний, в результате каждого из которых с вероятностью () происходит событие. Интегральная...
-
Ответ: y=f(kx) получается из Графика функции f(x) сжатием его вдоль оси ох в k раз, если k>1 и растяжением в 1 деленную на k раз, если k>0 но меньше 1....
-
Теорема о параметризации - Рекурсивные функции
Одно и то же выражение может порождать несколько разных функций, от разного числа аргументов. Так, обычное арифметическое выражение xK можно считать...
-
Теорема Пенлеве - Условия Фукса и теорема Пенлеве
Все приведенные выше исследования велись в предположении, что мы изучаем поведение интеграла в области изменения z, при котором w(z) принимает вполне...
-
Бесконечные пределы - Свойства функций
Функция называется Бесконечно малой при (или, или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех...
-
В данной работе доказывается методами элементарной математики "большая" или "последняя" теорема Ферма. Некоторая, излишняя в обычных случаях, подробность...
-
В 1930 году Дж. Биркгофом и Дж. фон Нейманом была сформулирована и доказана одна из основных эргодических теорем - теорема о предельных вероятностях:...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
У цьому параграфі узагальнюються і уточнюються так звані "зворотні теореми" теорії наближення. Мова йде про оцінці диференціальних властивостей функції f...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Условия Фукса - Условия Фукса и теорема Пенлеве
Интегралы уравнения вида (1) Не имеют критических подвижных точек. Если в раскрытом виде уравнение (1) (2) И если содержит w, то интегралы уравнения (2)...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
Теоремы Ферма, Ролля, Лагранжа и Коши