О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно-монотонную функцию f1(x) с периодом 2м b - a, совпадающую с функцией f (x) на отрезке [a, b].
Разложим функцию f1(x) в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] (кроме точек разрыва) совпадает с заданной функцией f (x), т. е. мы разложили функцию f (x) в ряд Фурье на отрезке [a, b].
Рассмотрим, далее, следующий важный случай. Пусть функция f(x) задана на отрезке [0,l]. Дополняя определение этой функции произвольным образом на отрезке [-l,0] (сохраняя кусочно монотонность), мы можем разложить эту функцию в ряд Фурье. В частности, если мы продолжим определение функции f(x) при так: f(x) = , то получим нечетную функцию, которая разлагается по синусам. (Функция f(x) "продолжена нечетным образом").
Практика:
Разложим исходную функцию f (x) в ряд Фурье по тригонометрической системе функций на [-1;1].
- 1) Найдем коэффициенты Фурье: 2) Раскладываем функцию f(x) в ряд Фурье:
Ответ:
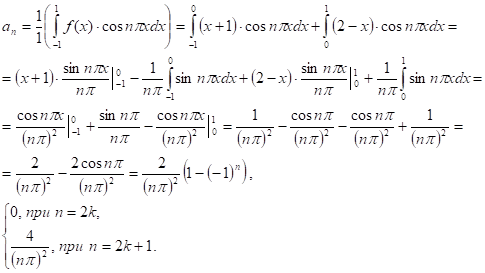
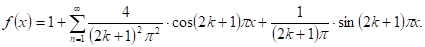
А) Нарисовать график функции f(x) на отрезке [-1;1].
Теория:
Определение. Функция f (x) называется Кусочно-монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек x, x, ..., x на интервале (a, x), (x1, x2), ..., (xN-1, b) так, что на каждом из интервалов функция монотонна, т. е. либо невозрастающая, либо неубывающая.
Практика:
Построим график данной функции:
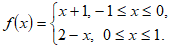
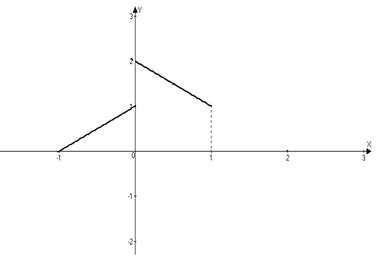
Б) Написать к чему сходится этот ряд Фурье в точках отрезка [-1;1].
Теория:
Определение. Функция f (x) называется удовлетворяющей условиям Дирикле на сегменте [a, b], если:
- 1. функция непрерывна на сегменте [a, b] или кусочно-непрерывна (т. е. имеет на нем конечное число точек разрыва 1 рода); 2. функция кусочно-монотонна на сегменте [a, b].
Теорема Дирикле: Пусть периодическая функция f (x) с периодом 2р удовлетворяет на любом сегменте условиям Дирихле. В таком случае ряд Фурье, соответствующий этой функции, сходится во всех точках числовой оси. При этом в каждой точке непрерывности функции f(x) сумма ряда S(x) равна значению функции в этой точке. В каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x>x0 слева и справа, т. е.: S(x) = 0,5[f(x0 + 0)+f(x0 - 0)].
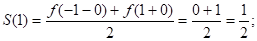
Практика:
В каждой точке отрезка [-1;1] полученный ряд сходится к значению функции f(x) в точках:
Ответ:
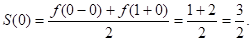
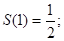
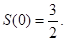
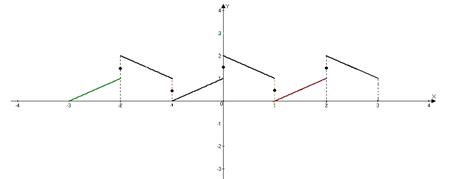
В) Нарисовать график суммы ряда на отрезке [-3, 3].
Теория:
Как уже было сказано, в каждой точке непрерывности функции f(x) сумма ряда S (x) равна значению функции в этой точке. В каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x>x0 слева и справа.
Практика:
Г) Пользуясь равенством Парсеваля, найти сумму:
Теория:
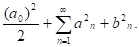
Для функции f(x), такой, что f2(x)L(-;), справедливо равенство Парсеваля:
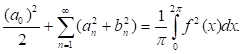
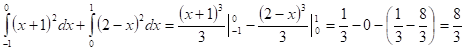
Практика:
Ответ: 8/3.
Задание № 4
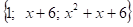
Найти линейную комбинацию функций, дающую наилучшее приближение по норме функции F(x) =x3+2x2+6x+4 на отрезке
[-1;1].
Теория:
Бесконечная система функций Ц1(x), ц2(x), ..., цN(x) называется ортогональной на отрезке [a, b], если при любых n ? k выполняется равенство
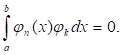
При этом предполагается, что
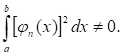
Пусть функция F(x), определенная на отрезке [a;b], такова, что
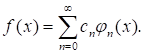
При этом:
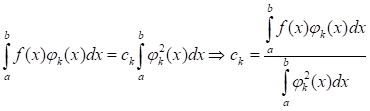
Коэффициенты cN, вычисленные по данной формуле называют коэффициентами Фурье функция F(x) По системе ортогональных функций. А ряд из первой формулы называют рядом Фурье по системе функций.
Практика:
Построим по данной системе ортогональную систему функций.
Найдем ортогональный базис :
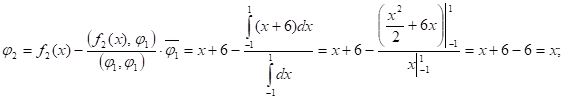
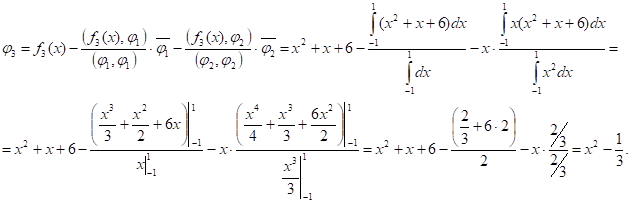
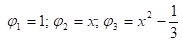
Система функций: - ортогональная система на отрезке [-1,1].
Наилучшее приближение по норме функции f(x) дает линейная комбинация:
, где - коэффициенты Фурье.
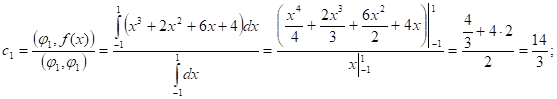
В итоге получаем:
Ответ:
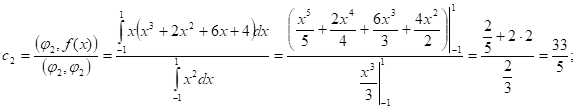
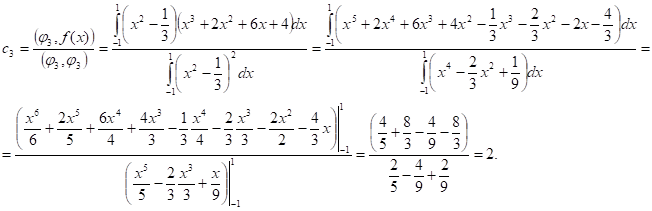
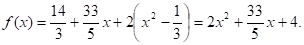
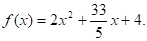
Задание №5
Найти объем тела, заданного системой неравенств:
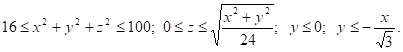
Теория:
Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Пусть в области V и на ее границе определена некоторая непрерывная функция f(x, y, z), где x, y, z - прямоугольные координаты точки области. Для ясности в случае, если f(x, y, z)0, мы можем считать эту функцию плотностью распределения некоторого вещества в области V.
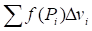
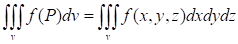
Разобьем область V произвольным образом на области, обозначая символом не только самую область, но и ее объем. В пределах каждой частичной области выберем произвольную точку и обозначим через значение функции f в этой точке. Составим интегральную сумму вида (1) и будем неограниченно увеличивать число малых областей так, чтобы наибольший диаметр стремился к нулю. Если функция f(x, y, z) непрерывна, то при этом будет существовать предел интегральных сумм вида (1). Этот предел, не зависящий ни от способа разбиения области V, ни от выбора точек, обозначается символом (2) и называется тройным интегралом.
Если подынтегральная функция f(x, y, z)=1, то тройной интеграл по области V выражает объем области V:
Похожие статьи
-
Симплекс - метод - Интегральное и дифференциальное исчисление
Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Вычисление тройного интеграла в декартовых прямоугольных координатах сводится к последовательному вычислению одного однократного и одного двойного...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
Итак, вышеизложенный материал наглядно рассматривает все интересующие нас разделы программы. Используя его, даже несведущий человек сможет овладеть...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Непрерывность функции - Свойства функций
Рассмотрим функцию, определенную на промежутке Пусть. Функция называется непрерывной в точке, если Функция называется Непрерывной слева (справа) в точке,...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Введение - Интегральное и дифференциальное исчисление
Эта курсовая работа является продолжением углубленного изучения высшей математики. В ней рассматриваются не пройденные нами темы за 3семестра изучения...
-
Исследуем на экстремум функцию: 1. С помощью необходимого существования экстремума, т. е. из системы Найдем координаты стационарных (критических) точек:...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
ПОНЯТИЕ ФУНКЦИИ Если некоторому множеству значений поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество, то тогда...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Стереометрические задачи - Применение производной в решении геометрических задач
Рис.7 Задача 1.Определить наибольший объем цилиндра, вписанного в конус с радиусом основания и высотой [4]. Решение. Обозначим радиус основания...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством...
-
Сферические координаты - Интегральное и дифференциальное исчисление
Пусть Где R - радиус-вектор точки М , т. е. R - расстояние от точки М до начала координат: Ц - угол между положительными направлением оси 0X и лучом (-...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Ответ: Функция f ставит в соответствие числу х число у, а функция g числу у число z. Говорят что h есть сложная функция составленная из функций g и f, и...
-
Несобственные интегралы, Интегрирование неограниченных функций - Определенные интегралы
При рассмотрении задачи интегрирования непрерывных и кусочно-непрерывных функций предполагалось, что эти подынтегральные функции являются ограниченными...
-
ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИЙ Функция называется Возрастающей на некотором Промежутке , если на этом промежутке большему значению независимой переменной...
О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач